Определение ускорения точки

Ускорением точки называется векторная величина , характеризующая быстроту изменения вектора скорости.

Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость V, а в момент времени t₁ приходит в положение М₁ и имеет скоростьV₁ (рисунок 1.3). Тогда за промежуток времени t=t₁–t скорость точки получает приращение

Рисунок 1.3

Для построения вектора отложим от точки М вектор , и построим параллелограмм, в котором диагональю будет , а одной из сторон , тогда вторая сторона будет изображать вектор . Следует отметить, что вектор всегда направлен в сторону вогнутости траектории.

Отношение приращения вектора скорости к соответствующему промежутку времени t определяет вектор среднего ускорения точки, за этот промежуток времени.

(1.5)

Вектор среднего ускорения имеет тоже направление, что и вектор , т.е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени или мгновенным ускорением называется векторная величина , к которой стремится среднее ускорение при стремлении промежутка времени t к нулю.

(1.6)

Следовательно, вектор мгновенного ускорения точки равен первой производной от вектора мгновенной скорости или второй производной от радиуса-вектора точки по времени.

Размерность ускорения м/с².

При прямолинейном движении точки вектор ускорения точки направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения , также как и вектор лежит в плоскости этой кривой и направлен в сторону её вогнутости.

1.2 Координатный способ задания движения точки

Положение точки можно непосредственно определять её декартовыми координатами X,Y,Z, которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. её положение в пространстве в любой момент времени, надо знать значение координат точки в каждый момент времени, т.е. знать зависимости:

X=f₁(t); Y=f₂(t); Z=f₃(t) (1.7)

которые представляют собой уравнения движения точки в прямоугольных декартовых координатах (рисунок 1.4).

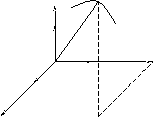M

z

z

y

о

x

y

x

Рисунок 1.4

Эти уравнения представляют собой закон движения точки при координатном способе задания движения.

Если движение точки происходит на плоскости XOY, то в этом случае будет два уравнения движения:

X = f₁ (t) и Y = f₂ (t) (1.8)