
Завдання для типового розрахунку
1.а) Для заданого визначника знайти мінор та алгебраїчне доповнення елементів ai2 та a3j.
b)Обчислити визначник розкриттям за j-м стовпцем, попередньо одержавши в ньому якомога більше нулів.
2. Обчислити
-
AB
-
BA
-
A-1
-
AA-1
-
A-1A
3. Перевірити сумісність системи та розв'язати її методами:
-
Крамера
-
Гаусса.
4. Перевірити сумісність системи та розв'язати її методами:
-
Матричним
-
Гаусса.
5,6. Розв'язати однорідну систему лінійних рівнянь.
Варіант 1
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6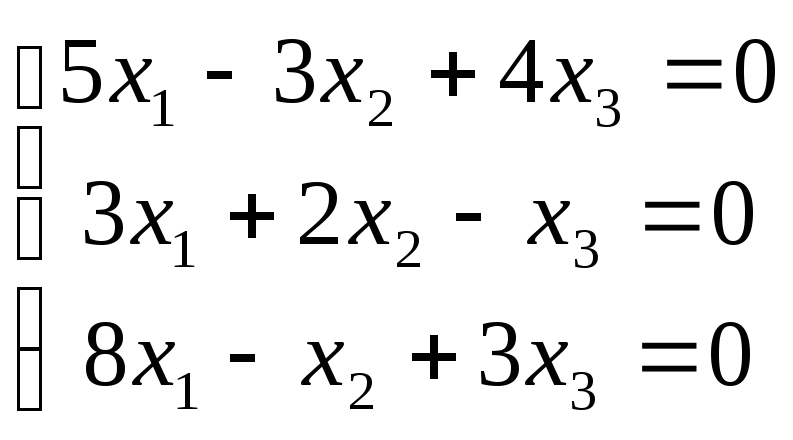 .
.
Варіант 2
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 3
1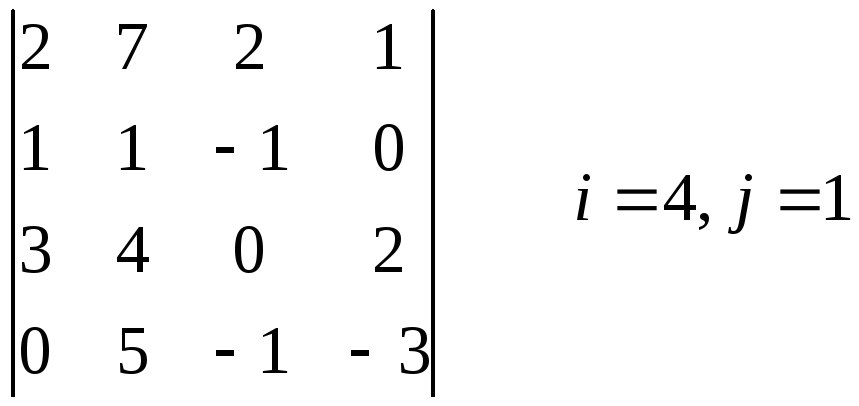 .
.
2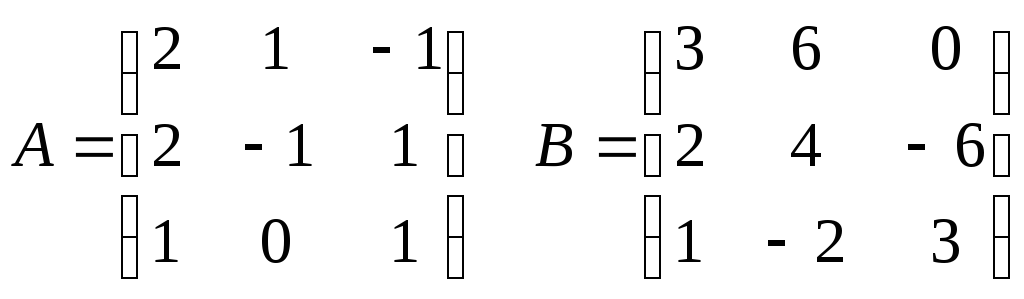 .
.
3 .
.
4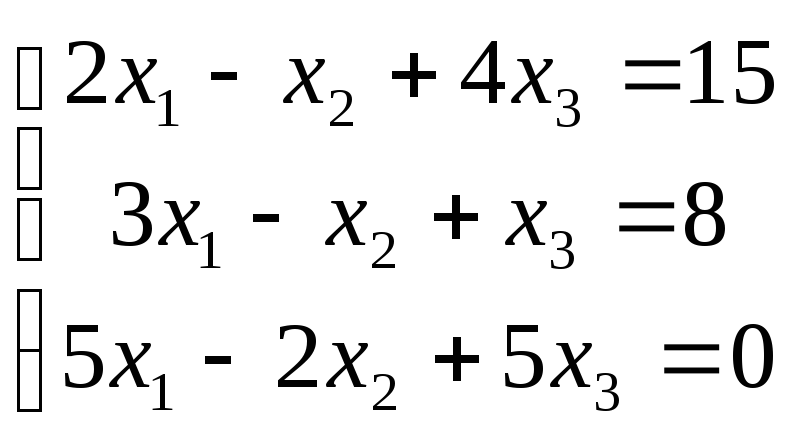 .
.
5 .
.
6 .
.
Варіант 4
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 5
1 .
.
2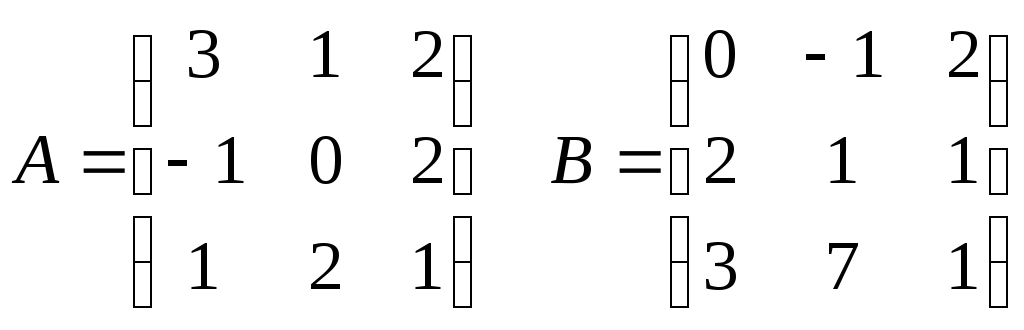 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 6
1 .
.
2 .
.
3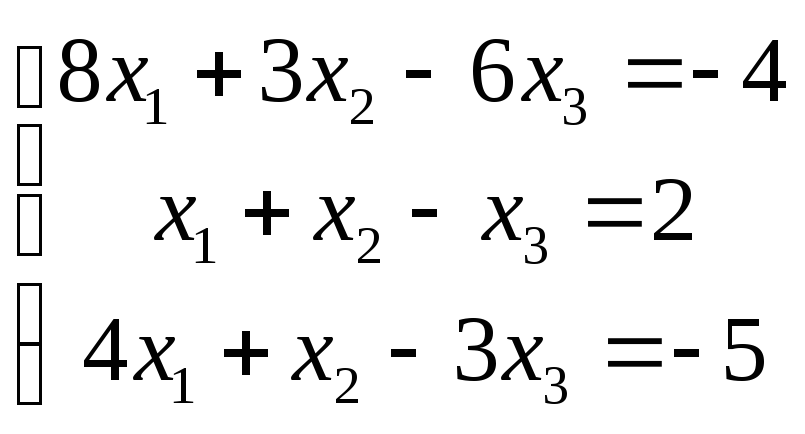 .
.
4 .
.
5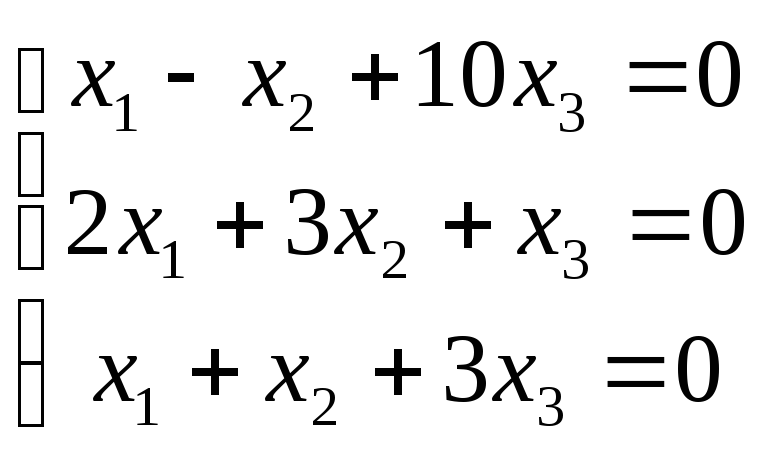 .
.
6 .
.
Варіант 7
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 8
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6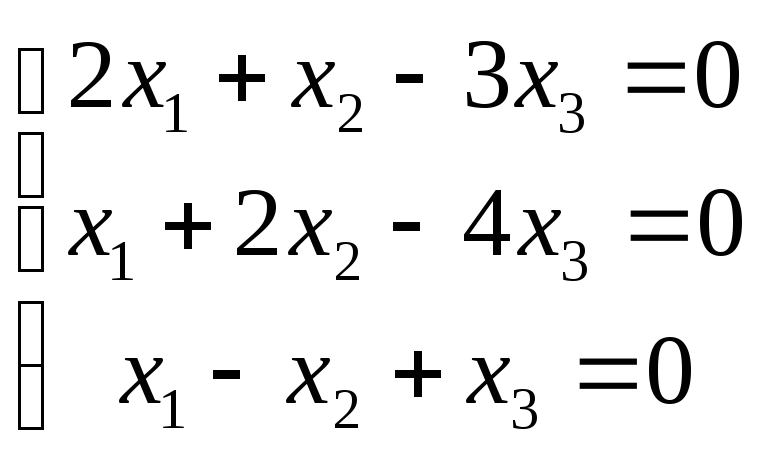 .
.
Варіант 9
1 .
.
2 .
.
3 .
.
4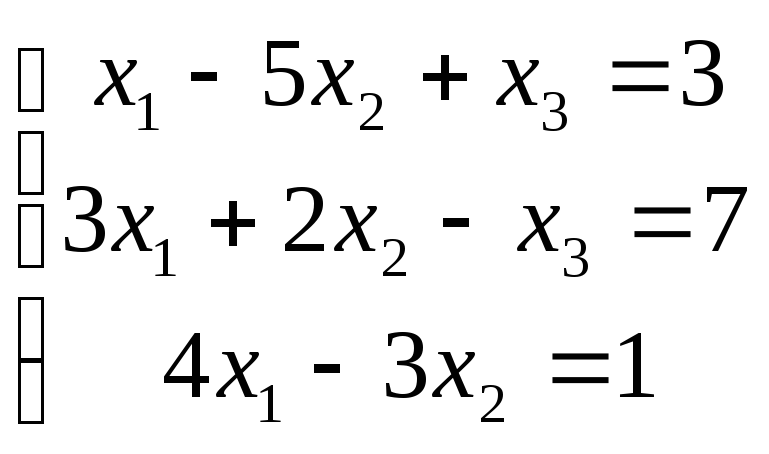 .
.
5 .
.
6 .
.
Варіант 10
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 11
1 .
.
2 .
.
3 .
.
4 .
.
5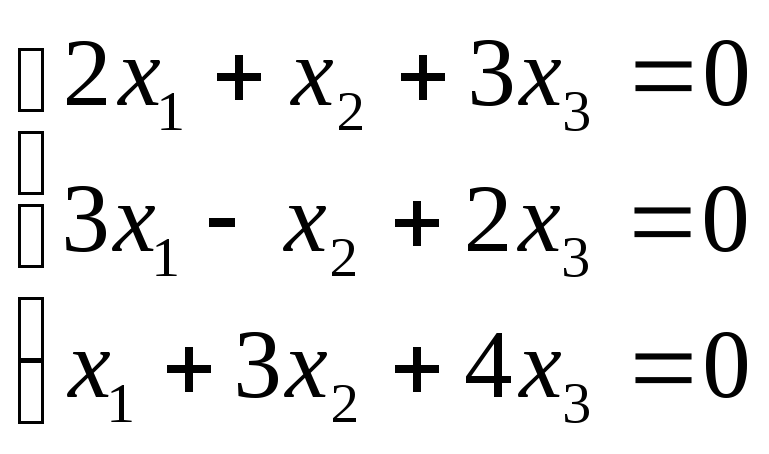 .
.
6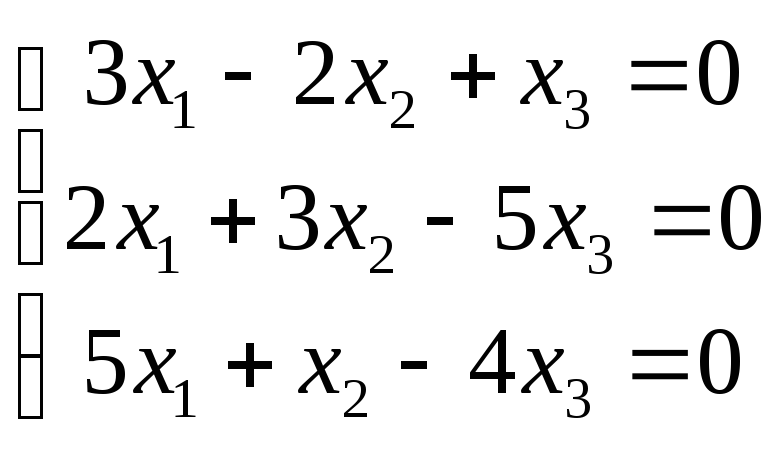 .
.
Варіант 12
1 .
.
2 .
.
3 .
.

4.
5 .
.
6 .
.
Варіант 13
1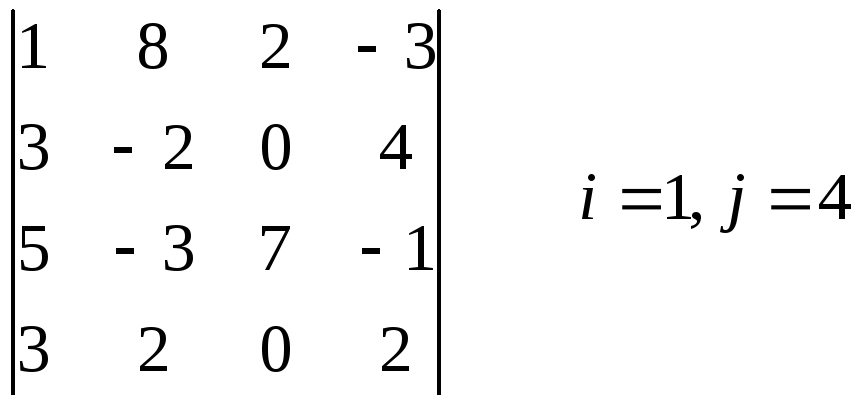 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 14
1 .
.
2 .
.
3 .
.
4 .
.
5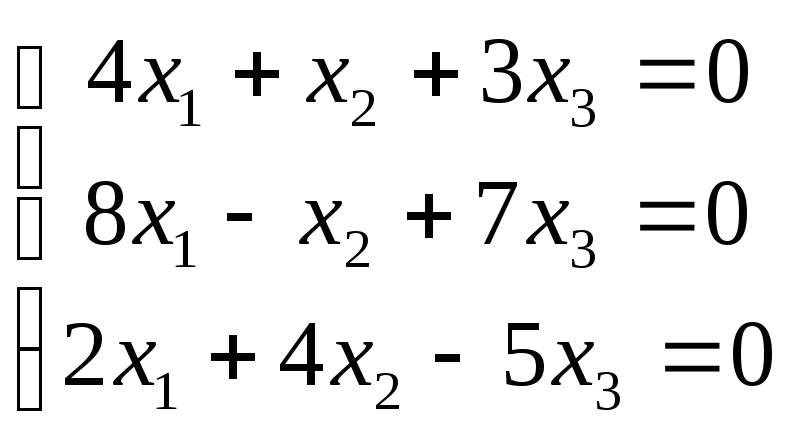 .
.
6 .
.
Варіант 15
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 16
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6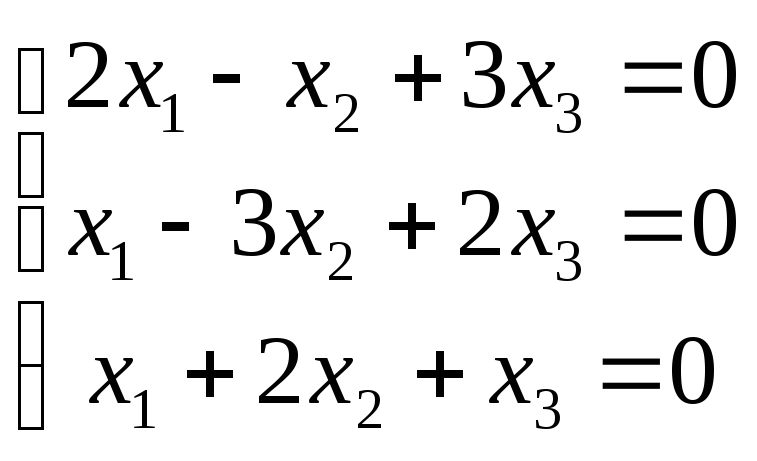 .
.
Варіант 17
1 .
.
2 .
.
3 .
.
4 .
.
5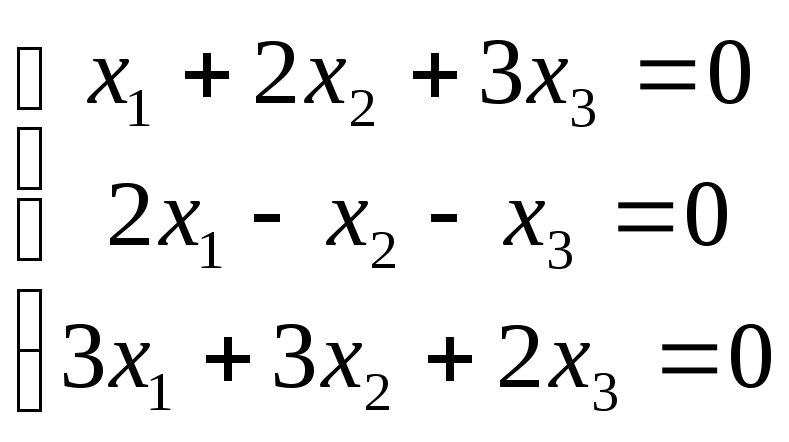 .
.
6 .
.
Варіант 18
1 .
.
2 .
.
3 .
.
4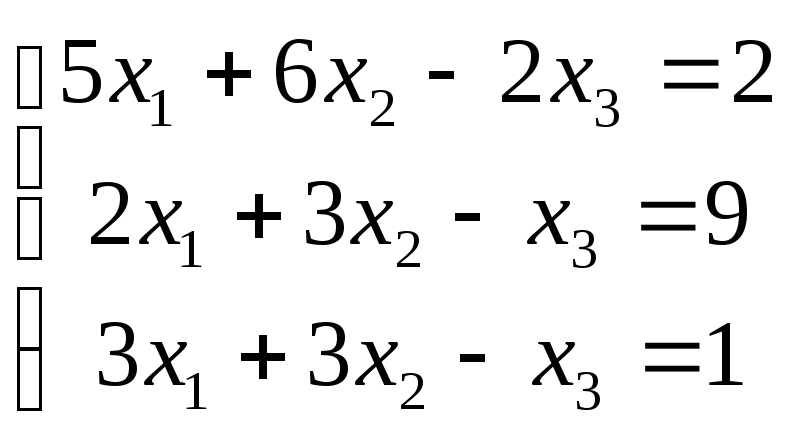 .
.
5 .
.
6 .
.
Варіант 19
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 20
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 21
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 22
1 .
.
2 .
.
3 .
.
4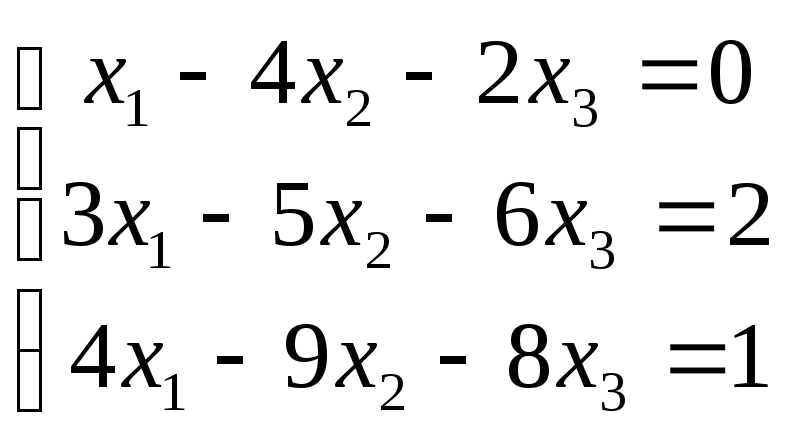 .
.
5 .
.
6 .
.
Варіант 23
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6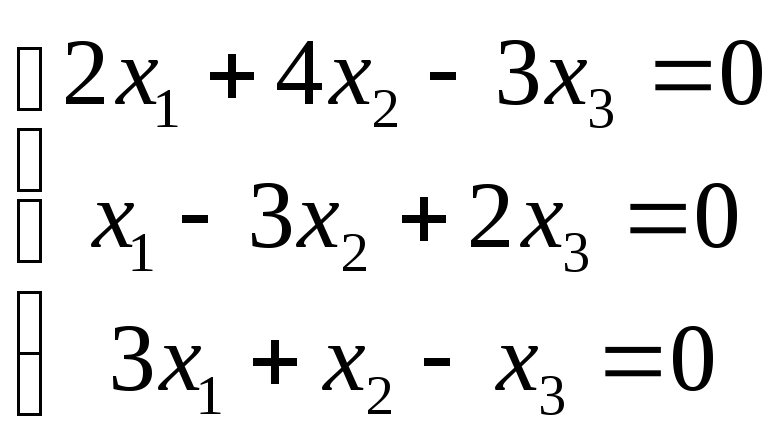 .
.
Варіант 24
1 .
.
2 .
.
3 .
.
4 .
.
5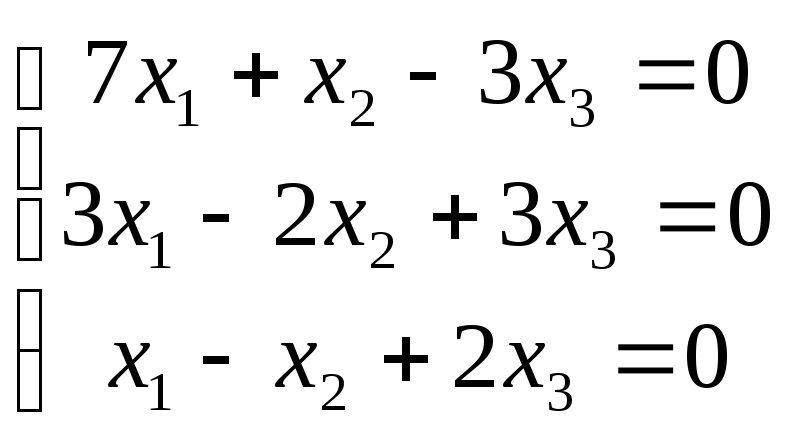 .
.
6 .
.
Варіант 25
1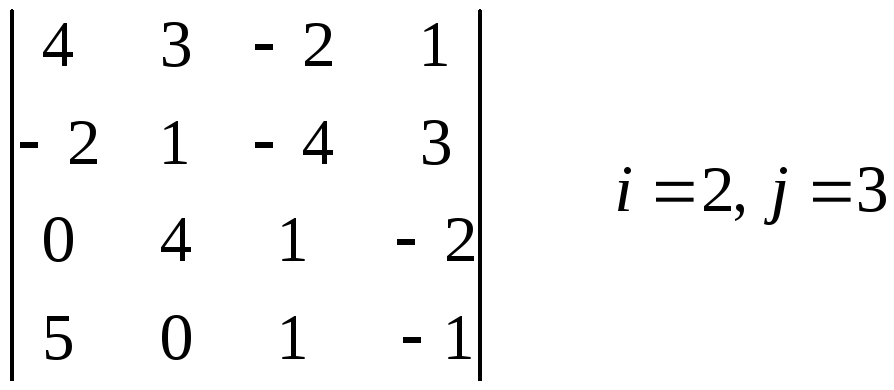 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 26
1 .
.
2 .
.
3 .
.
4 .
.
5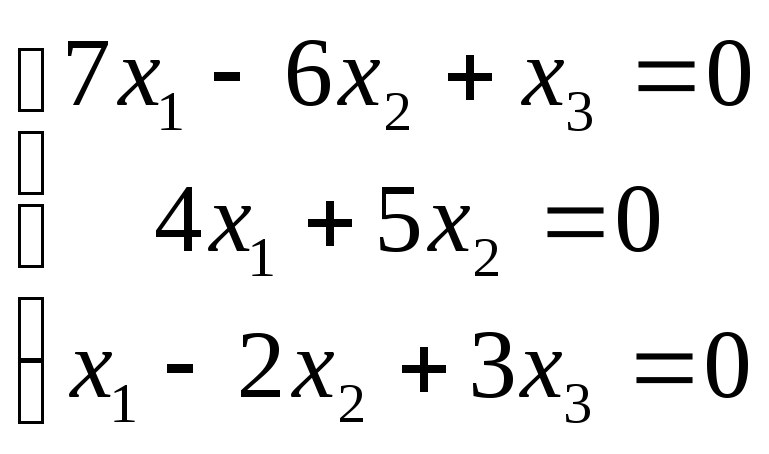 .
.
6 .
.
Варіант 27
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6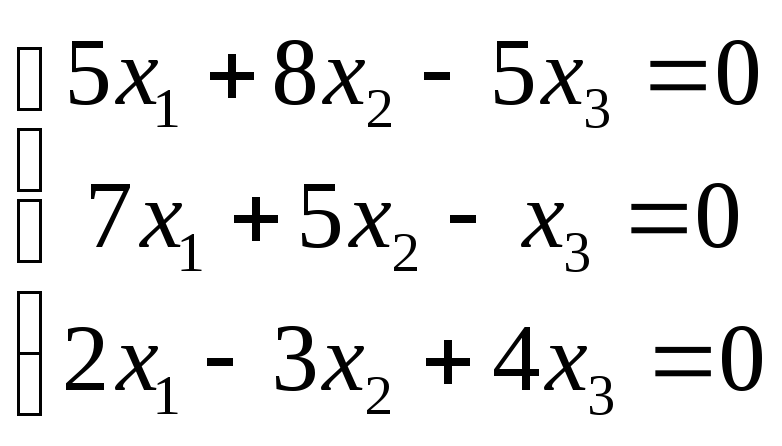 .
.
Варіант 28
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Варіант 29
1 .
.
2 .
.
3 .
.
4 .
.
5 .
.
6 .
.
Приклад розвязку типового розрахунку
1.а) Для заданого визначника знайти мінор та алгебраїчне доповнення елементів ai2 та a3j.

а) Для елементів a22 та a33 мінори дорівнюють:


Алгебраїчні доповнення:
![]() ,
,
![]() .
.
b)Обчислити визначник розкриттям за j-м стовпцем, попередньо одержавши в ньому якомога більше нулів.

Перетворимо спочатку визначник, використовуючи його властивості. Відіймемо від першого та другого рядка третій рядок , помножений на 2, а потім до четвертого додамо третій помножений на 2. Тепер розкладемо визначник за елементами третього стовпця та отримаємо визначник третього порядку, який розкриваємо за правилом Саріуса.
2. Обчислити
-
AB
-
BA
-
A-1
-
AA-1
-
A-1A

-
AB

b) BA

с) A-1
А11=-8
А12=8
А13=8
А21=-7
А22=0
А23=-7
А31=-10
А32=-32
 А33=-18
А33=-18

d)
AA-1
(Перевіримо
розрахунки![]() ).
).
d
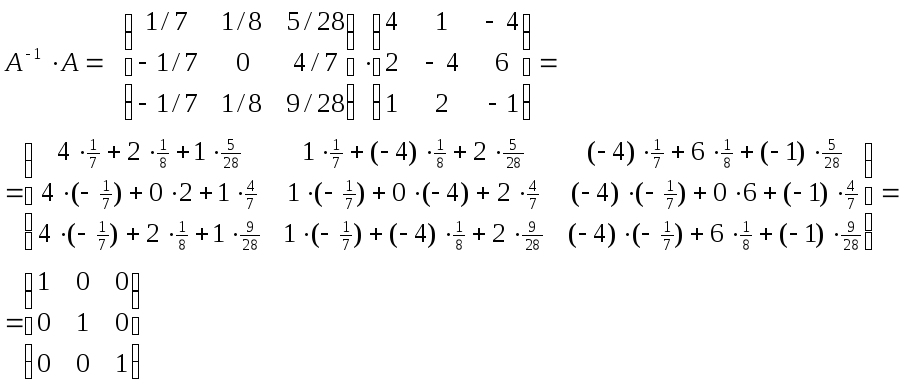 )
)
3. Перевірити сумісність системи та розв'язати її методами:
-
Крамера
-
Гаусса.

Щоб перевірити сумісність системи потрібно визначити ранг А та В.

Отже ранг матриці А та матриці В дорівнює 3. Тому за теоремою Кронекера – Капеллі система сумісна, причому має єдиний розв’язок.
-
Знайдемо визначники за правилом Саріуса:



Т аким
чином,
за
методом Крамера:
аким
чином,
за
методом Крамера:
![]()
![]()
![]()
Зробимо перевірку:

b) Використаємо елементарні перетворення.

Повернемося до системи лінійних рівнянь:

звідкіля x3=-1; x2=3; x1=0.

4. Перевірити сумісність системи та розв'язати її методами:
А)Матричним
Б)Гаусса.

Отже ранг матриці А дорівнює 3, а матриці В дорівнює 3. Тому за теоремою Кронекера – Капеллі система несумісна.
5. Розв'язати однорідну систему лінійних рівнянь.

Знайдемо визначник матриці А.

Отже оскільки визначник не дорівнює, 0 то система має єдиний розвязок х1=0, х2=0, х3=0.
6. Розв'язати однорідну систему лінійних рівнянь.

Знайдемо визначник матриці А.

Тобто система має безліч розв’язків. Знайдемо їх.

Повернемося до системи лінійних рівнянь:

Отже оскільки х3 може бути будь-яким, позначимо його через t. Тоді
![]() ,
,
![]() .
.
