2. Визначники та їх властивості

Визначником квадратної матриці другого порядку

називається число, яке дорівнює а₁₁а₂₂ –а₁₂а₂₁ та позначається

.

Числа a₁₁, a₁₂, a₂₁,a₂₂ називаються елементами визначника матриці другого порядку.

Визначник квадратної матриці також називають детермінантом. Для визначника матриці А застосовують наступні позначення

Визначником квадратної матриці третього порядку

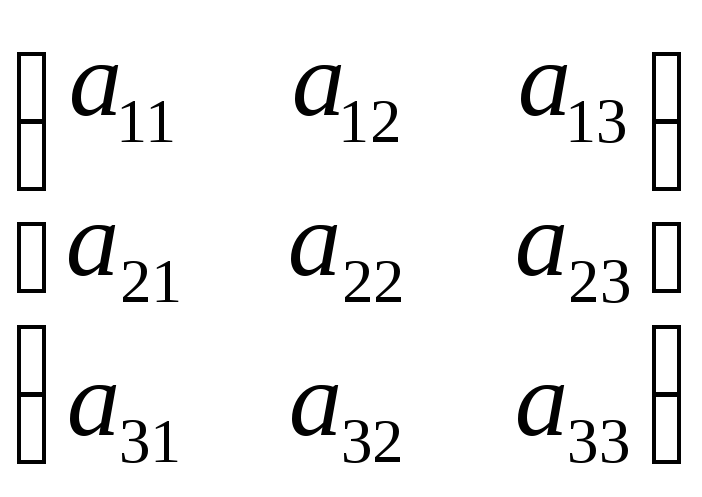
називають алгебраїчну суму усіх можливих n! добутків елементів взятих по одному з кожного рядка та кожного стовпця:

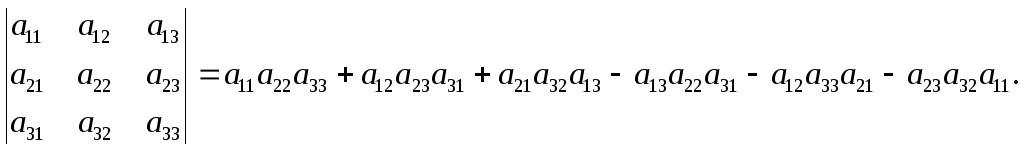
Це правило називається правилом Саріуса. Схематично можливо зобразити на рис.1.

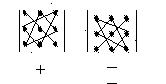
Рис.1.

Виродженою називається матриця, визначник якої дорівнює нулю. У протилежному випадку матриця є невироджена.

Мінором якого-небудь елементу визначника називається визначник, який утворюється з початкового шляхом викреслення рядка та стовпця, яким належить даний елемент. Мінор позначається М.

Алгебраїчне доповнення елемента а_ik визначника називається мінор зі своїм знаком, який визначається як (-1)^i+k :

А_ik=(-1)^i+k M_ik

Властивості визначників:

1. визначник не змінюється при зміні всіх рядків відповідними стовпцями;

2. при перестановці двох рядків (стовпців) визначник змінює знак;

3. визначник з двома однаковими рядками (стовпцями) дорівнює нулю;

4. множник, загальний для всіх елементів рядка (стовпця), можна винести за знак визначника);

5. визначник дорівнює нулю, якщо всі елементи рядка або стовпця дорівнюють нулю);

6. визначник не зміниться, якщо до елементів деякого рядка (стовпця) додати відповідні елементи іншого рядка (стовпця);

7. визначник дорівнює сумі додатків елементів будь-якого рядка (стовпця) на їх алгебраїчне доповнення.

Властивість 7 можливо виразити формулою:

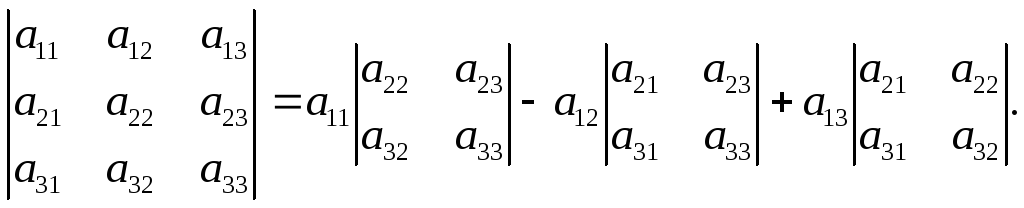
Надана формула представляє собою розклад визначника третього порядку за елементами першого рядка.

3. Обернена матриця.

Квадратна матриця А^-1 називається оберненою до квадратною матриці А, якщо виконується умова

А^-1 А= А А^-1=Е,

де Е – одинична матриця.

Квадратна матриця називається невиродженою або неособливою, якщо її визначник відрізняється від нуля. Якщо визначник матриці дорівнює нулю, вона називається виродженою або особливою.

Кожна невироджена матриця

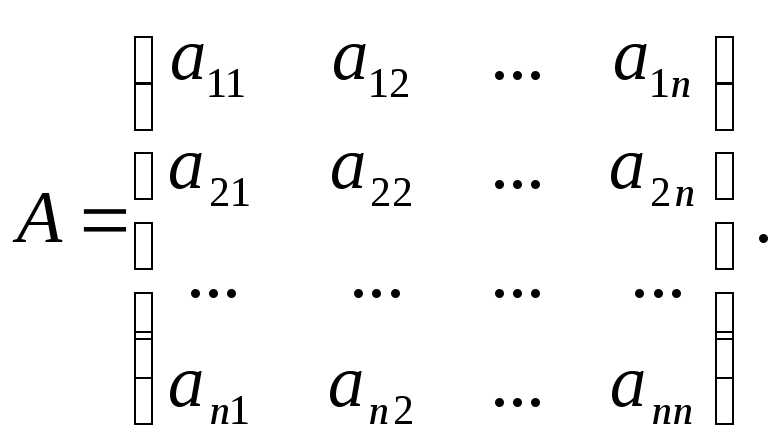
має обернену матрицю

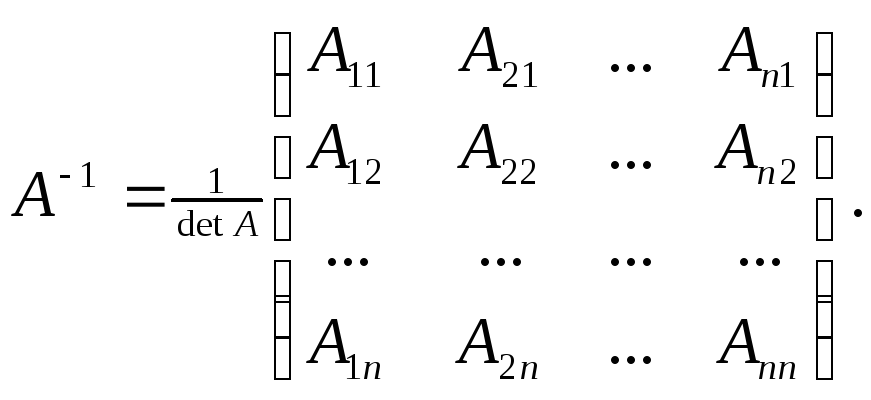
де А_ik- алгебраїчне доповнення елемента а_ik матриці А.

Матриця називається союзною або приєднаною:

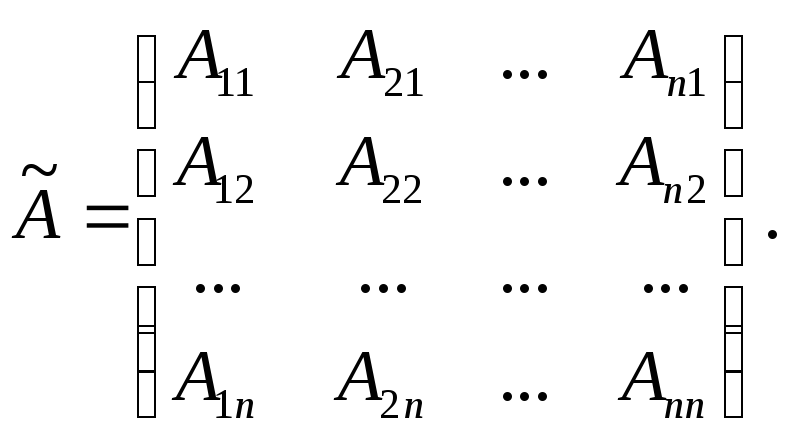
4. Ранг матриці

Рангом матриці називається найвищий з порядків її мінорів, який не дорівнює нулю.

Тобто якщо в матриці хоча б один мінор другого порядку дорівнює нулю, а всі мінори третього порядку дорівнюють нулю, то ранг такої матриці дорівнює двом.

Ранг позначається r(A).

Для підрахування рангу матриці використовують елементарні перетворення:

1. Транспонування.

2. Заміна місцями рядків або стовпців.

3. Множення рядка (стовпця) на число.

4. Додавання до рядка (стовпця) елементів паралельного стовпця помноженого на одне і теж число.

Всі ці операції ми можемо використовувати тому, що нас цікавить лише дорівнює мінор нулю чи ні.

Елементарними перетвореннями будь-яку матрицю можна привести до вигляду:

Ранг буде дорівнювати кількості рядків, що містять одиниці.