Лабораторна робота №1 Парна лінійна регресія

Лабораторна робота № 1

Тема роботи: Парна лінійна регресія.

Мета роботи: Навчитися будувати лінійні економетричні моделі, аналізувати їх і будувати прогнозні значення.

ЗАВДАННЯ

На основі статистичних даних показника Y і фактора Х вашого варіанту знайти:

• оцінки параметрів лінії регресії =b₀+b₁x;

• оцінки коефіцієнтів кореляції і детермінації;

• використовуючи критерій Фішера перевірити побудовану модель на адекватність з надійністю р=0,95;

Якщо модель адекватна, то:

• використовуючи t- тест Ст’юдента перевірити значимість параметрів b₀ і b₁ з надійністю р=0,95;

• побудувати інтервали довіри для параметрів β₀ і β₁ за t- тестом Ст’юдента з надійністю р=0,95;

• використовуючи t- тест оцінити значимість коефіцієнта кореляції з надійністю р=0,95;

• побудувати інтервали довіри для окремого прогнозного значення 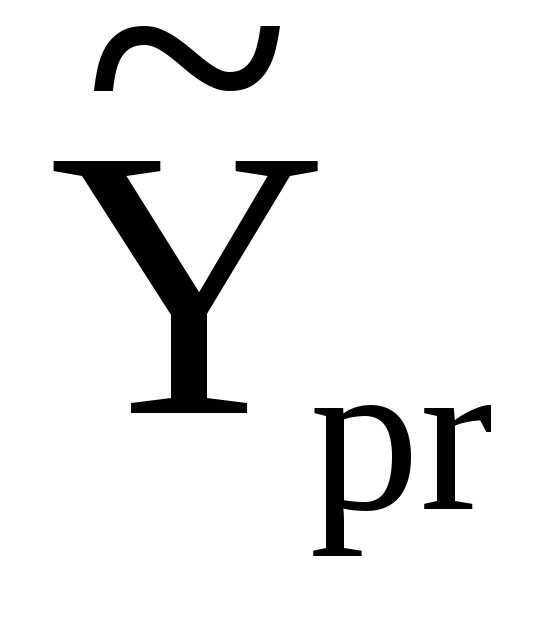і для математичного сподівання значення з надійністю р=0,95;

• побудувати надійні межі базисних середніх значень 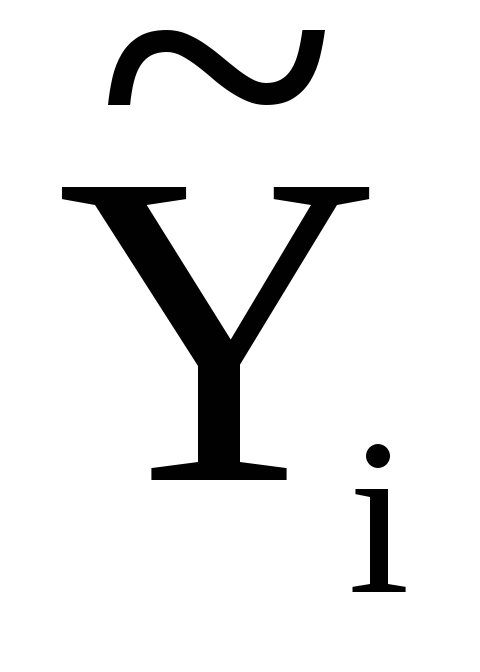з надійністю р=0,95 ;

• побудувати точкові графіки статистичних даних, лінії регресії і її довірчої зони.

На основі отриманих значень зробити висновки.

Приклад виконання роботи.

Бюро економічного аналізу фабрики “Світоч” оцінює ефективність відділу маркетингу з продажу цукерок. Для такої оцінки вони мають досвід праці у 5 географічних зонах з майже однаковими умовами (потенціальні клієнти, ставлення до товарного знака і т. ін.).У цих зонах вони зафіксували протягом однакового періоду обсяги продажів (млн. коробок), витрати (млн. грн.) фірми та просування товару на ринку. Дані наведені в таблиці 1.1.

Таблиця 1. 1 Початкові дані.

Витрати на рекламу (млн. грн), Хi	5	6	9	12	18	20
Обсяг продажу (млн. коробок), Yi	25	30	35	45	65	?

На основі статистичних даних показника Y і фактора Х знайти:

• оцінки параметрів лінії регресії =b₀+b₁x;

• оцінки коефіцієнтів кореляції і детермінації;

• використовуючи критерій Фішера перевірити побудовану модель на адекватність з надійністю р=0,95;

Якщо модель адекватна, то:

• використовуючи t- тест Ст’юдента перевірити значимість параметрів b₀ і b₁ з надійністю р=0,95;

• побудувати інтервали довіри для параметрів β₀ і β₁ за t- тестом Ст’юдента з надійністю р=0,95;

• використовуючи t- тест оцінити значимість коефіцієнта кореляції з надійністю р=0,95;

• побудувати інтервали довіри для окремого прогнозного значення і для математичного сподівання значення 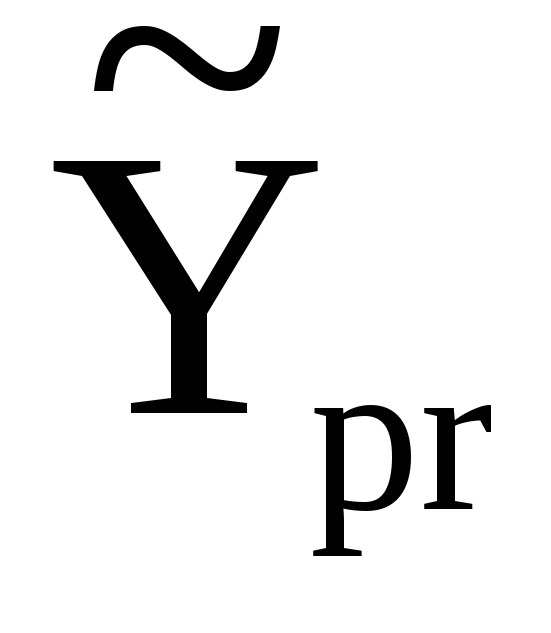для x_pr= 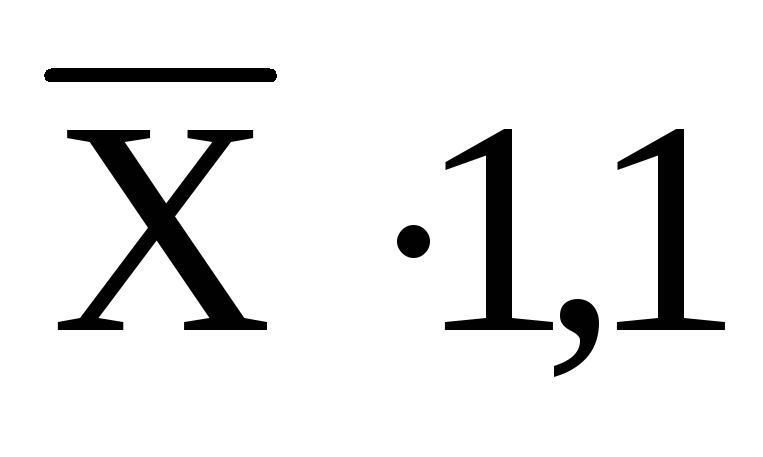з надійністю р=0,95;

• побудувати надійні межі базисних середніх значень з надійністю р=0,95 ;

• побудувати точкові графіки статистичних даних, лінії регресії і її довірчої зони.

На основі отриманих значень зробити висновки.

Хід роботи.

1. За умовою задачі припускаємо, що між даними є лінійна залежність, тобто їх можна апроксимувати прямою лінією. Взагалі, існує необмежена кількість прямих y=b₀+b₁x, які можна провести через множину спостережувальних точок. З множини можливих прямих оберемо “найкращу”. Для цього скористаємося методом найменших квадратів. Проведені попередні розрахунки подамо у вигляді таблиці 1.2:

Таблиця 1. 2 Допоміжні розрахунки.

	Витрати на рекламу (млн. грн), Хi	Обсяг продажу, (млн. коробок), Yi	X2i	XiYi
	5	25	25	125
	6	30	36	180
	9	35	81	315
	12	45	144	540
	18	65	324	1170
	20	?
	50	200	610	2330

Для знаходження невідомих параметрів b₀ і b₁ необхідно послідовно здійснити такі розрахунки:

b₁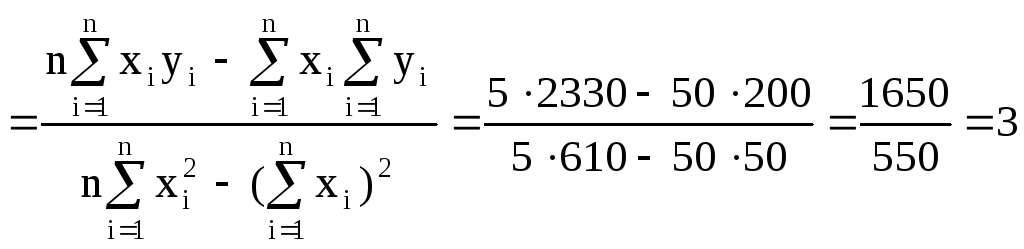

b₀=–b₁=40-3∙10=10.

Знаючи параметри b₀ і b₁, отриману пряму запишемо у вигляді:

Прокоментуємо, яким чином виконуються розрахунки за допомогою пакету Excel.

Для зручності розрахунків початкові статистичні дані розташуємо по стовпчикам у вигляді таблиці, яка обов’язково має свої заголовки і в кожному розмістимо у якості помітки змінну Х для незалежного фактора і Y для залежного (результату).

Для розрахунків значень параметрів b₀ і b₁ необхідно знайти значення наступних сум , , середні значення і .

Для цього введемо два нових стовпчика для додаткових розрахунків X_iY_i і , а потім у відповідні комірки введемо формули розрахунків:

D2: =B2^2;

E2: =B2*C2.

Використовуючи можливості копіювання зробимо копії цих формул у області D3:D6 і E3:E6 відповідно (Див. Додаток 1).

В комірці B8 розрахуємо суму значень фактору Х. Для цього:

• виділимо цю комірку;

• введемо знак =, а потім використавши список функцій викличемо функцію СУММ() (рис.1.1):

Рис 1. 1 Список функцій

• введемо параметри функції СУММ() (Рис.1.2):

Рис 1. 2 Введення параметрів функції СУММ()

• натиснемо Enter.

Виконаємо копіювання формули з комірки B8 в сусідні комірки C8:E8.

Для розрахунку середніх значень факторів X і Y використаємо функцію СРЗНАЧ(). Формулу, що містить цю функцію для Х помістимо в комірку C11, а для Y в C12:

C11: =СРЗНАЧ(B2:B6);

C12: =СРЗНАЧ(C2:C6).

В комірку C6 помістимо формула, що містить функцію для розрахунку кількості елементів в вибірці:

C6: =СЧЕТ(B2:B6).

Оскільки всі необхідні додаткові розрахунки є, в комірках C13 і С14 розрахуємо відповідні значення параметрів моделі b₁і b₀ відповідно (Див. Додаток 1 Додаток 2):

C13: =(C10*E8-B8*C8)/(C10*D8-B8^2);

C14: =C12-C11*C13.

2. Розрахуємо коефіцієнти кореляції та детермінації, скориставшись 5т.5..1.3

Таблиця 1. 3 Допоміжні розрахунки

	Витрати на рекламу (млн. грн), Хi	Обсяг продажу, (млн. коробок), Yi	X2i	XiYi	Y2i
	5	25	25	125	625
	6	30	36	180	900
	9	35	81	315	1225
	12	45	144	540	2025
	18	65	324	1170	4225
	20	?
	50	200	610	2330	9000

==0,995

r²=0,99

Дії для розрахунків значень подібні описаним вище:

F2: =C2^2;

….

F6: =C6^2;

F8: =СУММ(F2:F6);

C15: =(C10*E8-B8*C8)/(C10*D8-B8^2)^0,5/(C10*F8-C8^2)^0,5;

C16: =C15^2.

3. Для перевірки моделі на адекватність спочатку сформулюємо нульову гіпотезу: модель не є адекватною, тобто H₀ : _=0. Задамо рівень значимості, наприклад, 5%. Обчислимо F-відношення, скориставшись 5т.5..1.4.

Таблиця 1. 4 Допоміжні розрахунки

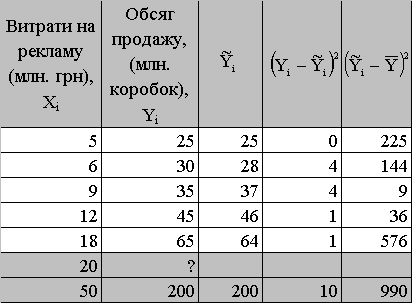
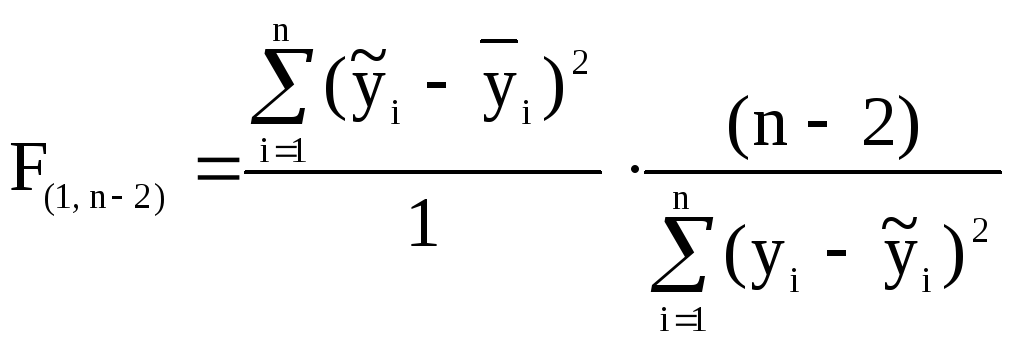==297.

Дії для розрахунків в Excel:

G2: =$C$14+$C$13*B2;

….

G6: =$C$14+$C$13*B6;

H2: =(C2-G2)^2;

….

H6: =(C6-G6)^2;

I2: =(G2-$C$12)^2;

….

I6: =(G6-$C$12)^2;

G8: =СУММ(G2:G6);

H8: =СУММ(H2:H6);

I8: =СУММ(I2:I6);

E10: =I8*(C10-2)/H8

Використовуючи функцію FРАСПРОБР() знаходимо F_кр. При заданому рівні значимості 5% та з (1,3) ступенями вільності (для простої лінійної регресії): F_кр.=10,13.

Надамо пояснення, що до аргументів функції FРАСПРОБР() (Рис. 1.3):

“Вероятность” – це аргумент, значення якого є імовірність помилки α=1-p;

“Степень свободы 1” – для парної лінійної регресії це значення дорівнює 1;

“Степень свободы 2” – це значення дорівнює n-2.

Рис 1. 3 Введення параметрів для функції FРАСПРОБР()

E11: =FРАСПОБР(0,05;1;C10-2)

Оскільки F>F_кр., нульову гіпотезу відкидаємо з 5%-ним ризиком помилитися, тобто побудована модель адекватна реальній дійсності.

4. Використавши t-тест 7т.’юдента перевіримо значимість параметрів лінії регресії, скориставшись розрахунками таблиці 1.5

Таблиця 1. 5 Допоміжні розрахунки

.

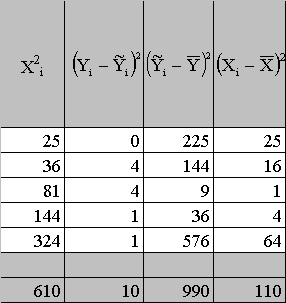
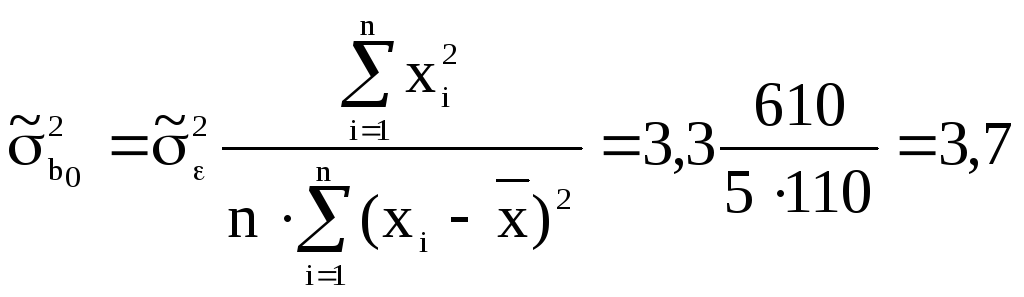
Розрахунки в Excel:

J2: =(B2-$C$11)^2;

….

J6: =(B6-$C$11)^2;

J8: =СУММ(J2:J6);

E12: =H8/(C10-2);

E13: =E12*D8/C10/J8;

E14: =E12/J8.

Розрахуємо значення t-статистики для кожного параметра:

.

Розрахунки в Excel:

E15: =C14/E13^0,5;

E16: =C13/E14^0,5.

Використовуючи статистичну функцію СТЬЮДРАСПОБР() знайдемо значення t_кр(0,95;3)=3,18 (Рис 1.4).

Надамо пояснення, що до аргументів функції СТЬЮДРАСПОБР():

“Вероятность” – це аргумент, значення якого є імовірність помилки α=1-p;

“Степень_свободы” – це значення дорівнює n-2.

Розрахунки в Excel:

G10: =СТЬЮДРАСПОБР(0,05;C10-2).

Оскільки обидва значення t- статистики більші ніж критичне значення, то можна зробити висновок, що отримані параметри є значимими і для генеральної сукупності параметри рівняння лінії регресії відрізняються від 0.

Знаючи, що для лінійної регресії F=, перевіримо вірність своїх розрахунків. Дійсно, F=297 і =17,2²=297.

Рис 1. 4 Введення параметрів для функції СТЬЮДРАСПОБР()

5. Побудуємо 95%-ий інтервал довіри для параметрів лінії регресії :

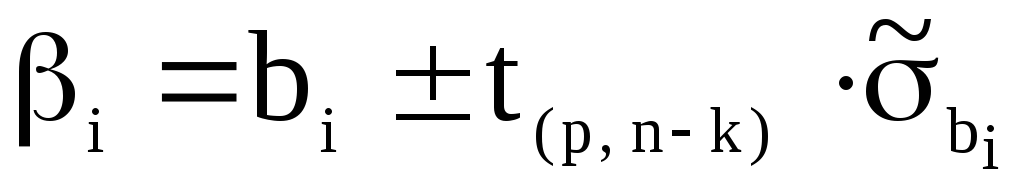₀=10±3,18·1,92 і ₁=3±3,18·0,17.

Отже, інтервали становлять:

3,88_16,12 і 2,45_3,55

Розрахунки в Excel:

F11: =C14-G10*E13^0,5;

H11: =C14+G10*E13^0,5;

F12: =C13-G10*E14^0,5;

H12: =C13+G10*E14^0,5.

6. Використовуючи t- тест 9т.’юдента перевіримо значимість коефіцієнта кореляції, тобто перевіряємо нуль-гіпотезу: H₀ :(коефіцієнт кореляції  для генеральної сукупності дорівнює 0) проти альтернативної : H₁ : 

t_r=.

Це значення співпадає зі значенням t_b1.

Розрахунки в Excel:

G13: =C15*(C10-2)^0,5/(1-C16)^0,5.

Раніш було отримано, що теоретичне значення t_kr з 3 ступенями вільності і 5%-ним рівнем значимості, яке дорівнює t_(0,95;3)=3,18. Оскільки t_r >t_(0,95;3), ми відкидаємо нуль-гіпотезу і робимо висновок, що коефіцієнт кореляції генеральної сукупності відрізняється від 0, тобто є значимим.

7. Розрахуємо точкову оцінку для прогнозного значення x_pr=20:

10+3·20=70 (G7: =$C$14+$C$13*B7).

Точність оцінки для окремого значення:

Δ=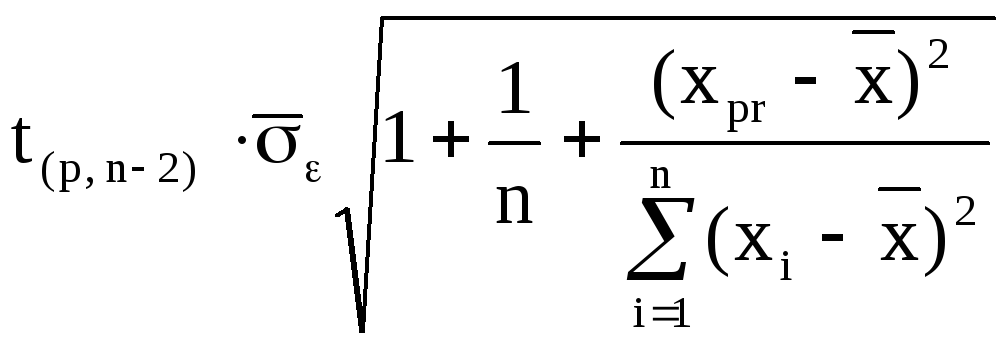==8,44.

J7: =(B7-$C$11)^2;

G14: =G10*E12^0,5*(1+1/C10+J7/J8)^0,5.

Інтервал довіри для окремого прогнозного значення =67±8,08 або :

61,5678,43.

F15: =G7-G14;

H15: =G7+G14.

Точність оцінки для математичного сподівання окремого прогнозного значення

Δ_M===6,12.

Інтервал довіри для математичного сподівання окремого прогнозного значення M або 63,8876,12.

G16: =G10*E12^0,5*(1/C10+J7/J8)^0,5;

F17: =G7-G16;

H17: =G7+G16.

8. Для побудови графіків нам знадобиться таблиця 1.6 з необхідними розрахунками, в яку розмістимо точність оцінки для математичного сподівання окремого базового значення, яке знайдемо за формулою:

Δ_Mi=.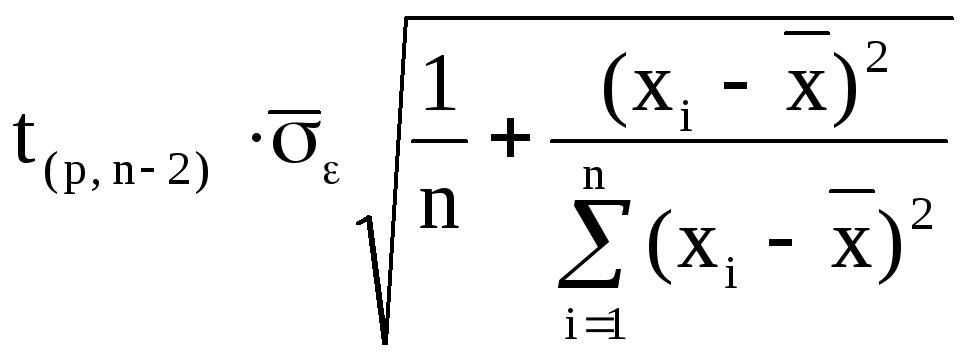

Розрахунки в Excel:

K2: =$G$10*$E$12^0,5*(1/$C$10+J2/$J$8)^0,5;

….

K7: =$G$10*$E$12^0,5*(1/$C$10+J7/$J$8)^0,5;

L2: =G2-K2;

….

L7: =G7-K7;

M2: =G2+K2;

….

M7: =G7+K7.

Таблиця 1. 6 Допоміжні розрахунки

Кінцеві графіки будуть мати наступний вигляд:

Рис 1. 5 Точкові графіки статистичних даних, лінії регресії і її довірчої зони.

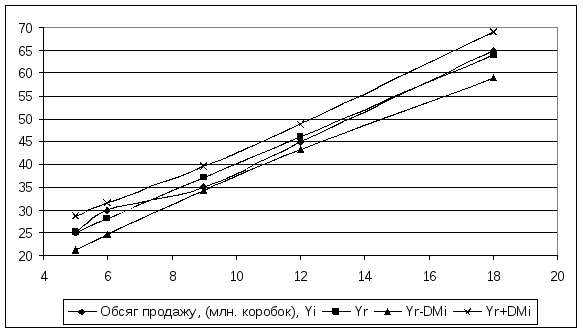
Зробимо деякі зауваження, що до побудови графіків:

• виділити одночасно області B1:C6; G1:G6; L1:M6;

• Визвати “Мастер диаграмм” і для побудови обрати “Точечная”;

• Отформотувати всі необхідні елементи діаграми, клацнувши правою кнопкою “Миші” на необхідному елементі діаграми і виконуючи команду “Формат …”