Лекция 23

Лекция 23. Понятие производной и её смысл (геометрический, физический, экономический). Производные элементарных функций. ( Вывод ). Таблица производных. Правила дифференцирования. Дифференциал и его смысл.

Дифференциальное исчисление – это раздел высшей математики, базирующийся на использовании таких ключевых для всей высшей математики понятий, как производные и дифференциалы функций. Эти понятия были введены в математику в конце 17 века Исааком Ньютоном и Готфридом Лейбницем.

Производная функции рассматривалась в школьном курсе математики. Поэтому сначала кратко повторим пройденное.

Пусть – некоторая непрерывная функция (ее график – сплошная линия) – рис. .1. Здесь (М₁, М₂, М₃,…) – вершины и впадины графика функции. А их проекции (x₁, x₂, x₃,…) на ось ох называются соответственно точками максимума и минимума функции. Эти точки имеют и общее название: точки экстремума функции. Повторим еще раз: точки экстремума (точки максимума и минимума) функции – это не вершины и впадины графика функции, а их проекции на ось ох.

Интервал оси ох, на котором с увеличением аргумента x растет и функция y, называется интервалом возрастания функции. А интервал оси ох, на котором с увеличением аргумента x функция y убывает, называется интервалом ее убывания. В частности, на рис. 1 интервалы () и (x₂; x₃) – интервалы возрастания функции , а интервалы (x₁; x₂) и () – интервалы ее убывания.

Функция, возрастающая (убывающая) на некотором интервале, считается возрастающей (убывающей) в каждой точке x этого интервала.

Заметим, что возрастая или убывая на интервале, функция делает это для разных x, вообще говоря, неодинаково быстро. Например, возрастающая на интервале (x₂; x₃) функция (рис. .1) сначала для x, близких к x₂, растет медленно (график функции поднимается медленно); затем, по мере увеличения x, крутизна подъема графика функции возрастает, а значит, увеличивается и скорость роста функции; затем, по мере приближения x к x₃, скорость роста функции снижается. В точке x₃ рост функции прекращается и затем, для , начинается убывание функции. И оно тоже, очевидно, происходит для разных x с разной скоростью.

Возникает естественная задача: оценить скорость изменения функции (скорость ее роста или убывания) в каждой точке x численно. Эта задача решена в конце 17 века Ньютоном и Лейбницем путем введения в математику понятия производной функции.

В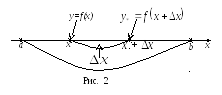спомним, как вводится это понятие. Пусть – некоторая непрерывная на интервале (a; b) оси ох функция. Если на этом интервале взять конкретное значение аргумента x (конкретную точку x), то в этой точке функция y получит конкретное значение . А теперь изменим x на некоторое , то есть перейдем от x к ( или ), причем возьмем такое, чтобы и точка тоже принадлежала интервалу (a; b) (рис.2).

Переход от x к означает, что аргумент x получил приращение (изменение) . При этом, естественно, и функция получит некоторое изменение (приращение) :

( 1)

Приращение функции , как и приращение аргумента , может быть любого знака – как положительным, так и отрицательным.

А теперь рассмотрим отношение , то есть отношение приращения функции к приращению аргумента. Это отношение показывает, на сколько единиц в среднем изменится y, если x изменится на единицу длины участка . То есть отношение определяет среднюю скорость изменения функции на участке оси ох.

Проиллюстрируем оправданность этого термина «средняя скорость» на механическом примере. Пусть функция определяет закон движения некоторой материальной точки по траектории ее движения, где x – время, а y – координата точки на траектории (рис. 3). Как и на реальной дороге, координату y точки на траектории ее движения можно понимать как удаленность этой точки от некоторой начальной точки О (от города, например). Зная закон движения движущейся точки, мы можем определить координату y этой точки в любой интересующий нас момент времени x. Тогда за время , прошедшее с момента x до момента , координата y движущейся точки изменится со значения до значения , то есть точка получит перемещение , определяемое формулой (1). Заметим, что это перемещение может быть и положительным, и отрицательным. Положительным оно будет, если точка удаляется от начальной точки О (у нее тогда будет расти y), а отрицательным – если точка приближается к точке О (у нее тогда y будет убывать). При этом средняя скорость движения за время (с момента x до момента ) будет равна

( 2 )

Одновременно отношение (2) является и средней скоростью изменения функции на участке .

Однако нас в конечном итоге интересует не средняя скорость изменения функции на участке, а истинная (мгновенная) скорость её изменения в заданной точке x. В частности, нас интересует мгновенная скорость движения точки по ее траектории (скорость в заданный момент времени x).

Чтобы получить эту скорость, нужно, очевидно, стянуть промежуток в точку x, то есть устремить к нулю. При этом, в силу непрерывности функции , и устремится к нулю, а отношение устремится к искомой мгновенной скорости изменения функции в точке х. То есть мгновенная скорость изменения функции в точке х - это

( 3 )

В частности, - это мгновенная скорость движения точки по ее траектории в момент времени х, если - закон движения точки.

Определение. Предел (3), представляющий собой мгновенную скорость изменения функции в точке х, называется производной функции в точке x. Используется несколько различных стандартных обозначений этой производной:

( 4 )

Последнее из этих обозначений использовал Ньютон, предпоследнее - Лейбниц, а первые три ввел французский математик Коши. В дальнейшем мы в основном для обозначения производной функции будем использовать обозначение Коши (или ), а при необходимости и (читается: производная функции y по переменной x).

Итак,

, ( 5 )

или подробнее

( 6 )

– математическое определение производной функции в заданной точке x. Читается это определение так: производная функции – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Если x – время, а y – координата движущейся точки на траектории ее движения (рис. 3), то функция определяет закон движения точки, а производная этой функции – мгновенную скорость движения точки по ее траектории:

( 7 )

В этом состоит физический смысл производной функции.

Но у производной функции есть и наглядный геометрический смысл. Для его выяснения рассмотрим рис. 4. Проведем к графику функции через точку и точку секущую , а через точку касательную L. Их углы наклона к оси ох обозначим соответственно и . Из следует:

( 8 )

Если устремить к нулю, то и устремится к нулю, а точка N устремится к точке M. Соответственно секущая устремится к касательной L, проведенной в точке M, а угол наклона секущей устремится к углу наклона касательной. То есть при . Но тогда

при ( 9 )

Иначе говоря,

, ( 10 )

что с учетом ( 5) дает

( 11 )

То есть производная функции в точке x – это угловой коэффициент касательной, проведенной к графику функции в точке графика с абсциссой x (см. рис. 5). В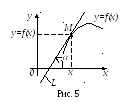 этом и состоит геометрический смысл производной функции.

Производной функции можно придать и наглядный экономический смысл, причем разносторонний.

1. Пусть, например, – количество произведенной продукции за время t. Тогда за время , прошедшее с момента t до момента , будет произведено единиц продукции. При этом отношение – это, очевидно, средняя производительность труда на промежутке времени длительностью . Она выражает среднее количество продукции, произведенной за единицу времени этого промежутка. А тогда предел

( 12 )

– это так называемая предельная (истинная) производительность труда в момент времени t.

2. Пусть x – количество выпускаемой продукции (в некоторых единицах), а y – соответствующие издержки на ее производство (в рублях). То есть y – себестоимость продукции x. Тогда – зависимость себестоимости продукции y от ее объема x.

Если объем продукции вырастет с x до , то есть вырастет на единиц, то ее себестоимость вырастет на рублей. Тогда – средняя себестоимость продукции, приходящаяся на единицу ее прироста. А

( 13 )

– так называемая предельная себестоимость продукции, определяющая затраты на производство единицы дополнительной продукции, если достигнутый объем производства составляет x единиц.

3. Пусть – так называемая кривая спроса, определяющая связь между ценой p единицы товара и спросом q на этот товар (q – количество товара, который может быть продан при цене p за его единицу) – рис. 6.

Кривая спроса, естественно, является убывающей кривой. Ее форма зависит от потребительских свойств товара, от финансового состояния покупателей и от других факторов. При этом

( 14 )

– суммарный доход от продаж. А

( 15 )

– так называемый предельный доход. Он определяет доход, полученный от единицы проданной продукции, если эта единица продана дополнительно к объему продаж q.

Эти и другие предельные величины широко используются в так называемом предельном экономическом анализе. В экономической литературе предельные величины называют также маржинальными. При их записи к обычному обозначению величин добавляется буква М. Например, MR – предельный доход R. И так как , то

( 16 )

Дифференцируемость функции в точке и на промежутке

Производная функции, согласно ее математического определения (5) и (6) – это некий предел. Но, как и всякий предел, он может оказаться:

а) конечным; б) бесконечным; в) вообще не существовать.

Если для данного x имеет место вариант (а), то есть если при заданном x производная функции существует и конечна, то эта функция называется дифференцируемой в точке x.

Функция, дифференцируемая в каждой точке x некоторого промежутка оси ох (например, интервала (a; b) или отрезка [a; b]) называется дифференцируемой на этом промежутке. Кстати, сама процедура вычисления производной функции называется ее дифференцированием (продифференцировать функцию – это значит найти ее производную).

Из геометрического смысла производной функции, определяемого равенством (11) и рис.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции в заданной точке x:

1. Существование касательной к графику функции в его точке с абсциссой x.

2. Не вертикальность этой касательной (ибо 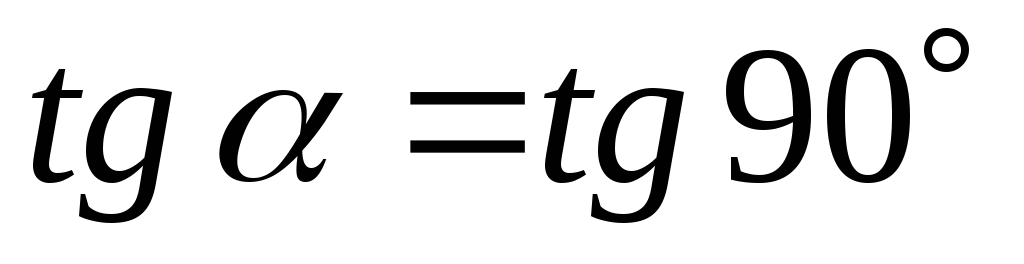не существует).

Например, функция , график которой изображен на рис.7, не дифференцируема в точках x₁, x₂ и x₃.

Действительно, точке x₁ соответствует на графике функции точка M₁ с вертикальной касательной. Точке x₂ (точке максимума функции) соответствует остроконечная вершина M₂, касательная в которой не существует. Точке x₃ соответствует точка M₃ – точка излома графика функции, в которой тоже касательная не существует.

Во всех же остальных точках M графика функции касательную к графику провести можно, и она не вертикальна. Значит, для всех остальных x, отличных от (x₁; x₂; x₃), существует производная функции. То есть во всех остальных точках x функция дифференцируема.

Непрерывность функций.

Определение. Функция у=f(x) называется непрерывной при значении х=х₀ (или в точке х₀), если она определена в некоторой окрестности точки х₀ ( очевидно, и в самой точке х₀) и если или, что то же самое, .

Геометрически непрерывность функции в данной точке означает, что разность ординат графика функции у=f(x) в точках и х₀ будет по абсолютной величине произвольно малой, если только будет достаточно мало.

Для непрерывных функций справедливы следующие теоремы, регламентирующие операции с этими функциями:

Теорема 1: Если функции и непрерывны в точке х₀, то сумма также есть непрерывная функция в точке х₀.

Теорема 2: Произведение двух непрерывных функций есть функция непрерывная.

Теорема 3: Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

Теорема 4: Если непрерывна при и f(u) непрерывна в точке , то сложная функция непрерывна в точке х₀.

Еще три теоремы описывают свойства непрерывных функций:

Теорема 5: Если функция y=f(x) непрерывна на некотором отрезке , то на отрезке найдется по крайней мере одна точка такая, что значение функции в этой точке будет удовлетворять соотношению, где х – любая другая точка отрезка, и найдется по крайней мере одна точка х₂ такая, что значение функции в этой точке будет удовлетворять соотношению . Значение функции будем называть наибольшим значением функции y=f(x) на отрезке , значение функции будем называть наименьшим значением функции на отрезке . (см. рис. 8)

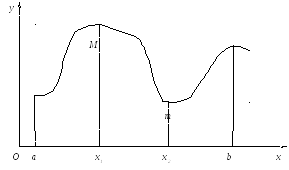
Рис. 8.

Теорема 6: Пусть функция непрерывна на отрезке и на концах этого отрезка принимает значения разных знаков, тогда между точками а и b найдется по крайней мере одна точка х=с, в которой функция обращается в нуль: .

Геометрический смысл этой теоремы в том, что график непрерывной функции , соединяющий точки и , где и ( или и ) пересекает ось ох по крайней мере в одной точке.

Рис.9.

Теорема 7: Пусть функция определена и непрерывна на отрезке . Если на концах этого отрезка функция принимает неравные значения , то каково бы ни было число , заключенное между числами А и В, найдется такая точка х=с, заключенная между а и b, что .

Геометрический смысл этой теоремы родственен теореме 6. В данном случае всякая прямая пересекает график функции .