§ 2. Волны в плотных материалах

Прежде всего я напомню вам об удобном способе описания синусоидальных плоских волн, которым мы пользовались в гл. 36 (вып. 3). Любая компонента поля в волне (возьмем, на­пример, Е) может быть записана в форме

E=E₀e^{i(t-k•r)}, (33.6)

где Е — амплитуда поля в точке г (относительно начала коор­динат) в момент t. Вектор k указывает направление распростра­нения волны, а его величина |k|=k=2 равна волновому числу. Фазовая скорость волны v_фаз=/k для света в материале с показателем n будет равна c/n, поэтому

k=n/c. (33.7)

Предположим, что вектор k направлен по оси z; тогда k•r будет просто хорошо знакомым нам kz. Для вектора k в любом другом направлении z следует заменить на r_k — расстояние от начала в направлении вектора k, т. е. kz мы должны заменить на kr_k, что как раз равно k•r (фиг. 33.2).

Фиг. 33.2. Фаза волны в точке Р, распространяющейся в направ­лении k, равна (t-k•r).

Таким образом, запись (33.6) является удобным представлением волны, идущей в любом направлении.

Разумеется, при этом мы должны помнить, что

k•r=k_xx+k_yy+k_:zz,

где k_x, k_y и k_z — компоненты вектора k по трем осям. Мы уже отмечали однажды, что на самом деле величины (, k_x, k_y, k_z) образуют четырехвектор и что его скалярное произведение на (t, x, у, z) является инвариантом. Таким образом, фаза волны есть инвариант и формулу (33.6) можно записать в виде

Однако сейчас нам такие хитрости не понадобятся.

Для синусоидального по­ля Е, подобного выражению (33.6), производная dE/дt — это то же самое, что и iE, a дЕ/дх — то же, что и ik_xE, и аналогично для остальных компо­нент. Вы видите, чем удобна форма (33.6): когда мы работаем с дифференциальными уравнениями, то дифференцирование заменяется простым умножением. Другое полезное качество состоит в том, что операция =(д/дx), (д/ду), (д/дz) заменяется тремя умножениями (-ik_x,-ik_y , -ik_z). Но эти три множителя преобразуются как компоненты вектора k, так что оператор  заменяется умножением на

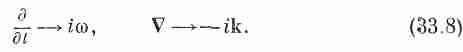
Правило остается справедливым для операции  в любой ком­бинации, будь то градиент, дивергенция или ротор. Например, z-компонента XЕ равна

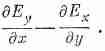
Если и Е_у и Е_х изменяются как e^-ik•r, то мы получаем

-ik_xE_y+ik_yE_x,

что представляет, как вы видите, z-компоненту —ikXЕ.

Таким образом, мы получили очень полезный общий закон, что в любом случае, когда вам нужно взять градиент от вектора, который изменяется, как волна в трехмерном пространстве (а они в физике играют важную роль), эту операцию вы можете проделать быстро и почти без всяких раздумий, если вспомните, что оператор  эквивалентен умножению на —ik.

Например, уравнение Фарадея

XЕ=дB/дt

превращается для волны в

— ikXЕ=-iB. Оно говорит, что

В=kXE/. (33.9)

Это соответствует результату, найденному ранее для волн в пу­стом пространстве, т. е. что вектор В в волне направлен под прямым углом к вектору Е и направлению распространения волны. (В пустом пространстве /k=с.) Знак в уравнении (33.9) вы можете проверить, исходя из того, что k является на­правлением вектора Пойнтинга S=₀c²(EXВ).

Если вы примените то же самое правило к другим уравне­ниям Максвелла, то снова получите результаты последней главы, в частности

Но раз уже это известно нам, давайте не будем проделывать все сначала.

Если вы хотите поразвлечься, можете попытаться решить та­кую устрашающую задачу (в 1890 г. она предлагалась студен­там на выпускных экзаменах): решите уравнения Максвелла для плоской волны в анизотропном кристалле, т. е. когда поля­ризация Р связана с электрическим полем Е через тензор поля­ризуемости. Конечно, в качестве ваших осей вы выберете глав­ные оси тензора, так что связи при этом упростятся (тогда Р_х=_aЕ_х, Р_у=_bЕ_у, a P_z=_cE_z), но направление волны и ее поляризация пусть останутся произвольными. Вы должны найти соотношение между Е и В и определить, как изменяется k с направлением распространения волны и ее поляризацией. После этого вам будет понятна оптика анизотропного кристалла. Лучше начать с более легкого случая дважды лучепреломляющего кристалла, подобного турмалину, для которого два коэффи­циента поляризуемости равны между собой (например, _b=_c), и попытаться понять, почему, когда мы смотрим через такой кристалл, мы видим два изображения. Если это вам удастся, тогда испытайте свои силы на более трудном случае, когда все три а различны. После этого вам уже будет ясен уровень ваших знаний — знаете ли вы столько же, сколько студент, заканчи­вавший университет в 1890 г. Но мы с вами в этой главе будем рассматривать только изотропные вещества.

Из опыта вам известно, что когда на границу раздела двух материалов, скажем воздуха и стекла или воды и бензина, попадает плоская волна, то возникают как отраженная, так и преломленная волны.

Предположим, что, кроме этого факта, нам больше ничего неизвестно, и посмотрим, что можно из него вывести. Выберем наши оси так, чтобы плоскость yz совпадала с поверхностью раздела, а плоскость ху была перпендикулярна фронту волны (фиг. 33.3).

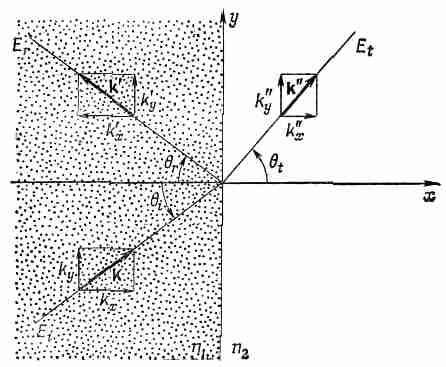
Фиг. 33.3. Векторы, распространения k, k' и k" для падающей, отраженной и прелом­ленной волн.

Электрический вектор в падающей волне может быть записан в виде

Поскольку вектор k перпендикулярен оси z, то

k•r=k_xx+k_yy. (33.12) Отраженную волну мы запишем как

так что ее частота равна ', волновое число k', а амплитуда Е'₀. (Мы, конечно, знаем, что частота и величина вектора k в отра­женной волне те же, что и в падающей волне, но не хотим пред­полагать даже это. Пусть это все получится само собой из мате­матического аппарата.) Наконец, запишем преломленную волну:

Вы знаете, что одно из уравнений Максвелла дает соотноше­ние (33.9), так что для каждой из волн

Кроме того, если показатели преломления двух сред мы обозна­чим через n₁ и n₂, то из уравнения (33.10) получится

Поскольку отраженная волна находится в том же ма­териале, то

в то время как для преломленной волны