Задачи и упражнения
1. Применяя метод непосредственного интегрирования, найти следующие интегралы:
a)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
.
2. Применяя метод замены переменной, найти следующие интегралы:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
;
и)
;
к)
;
л)
;
м)
.
3. Применяя метод интегрирования по частям, найти следующие интегралы:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
;
и)
.
Лекция 2. НеоПРЕДЕЛЕННЫЙ иНТЕГРАЛ
(продолжение)
План
-
Интегрирование выражений, содержащих квадратный трехчлен.
-
Интегрирование простейших рациональных дробей.
-
Интегрирование простейших иррациональных функций.
-
Интегрирование тригонометрических функций.
Ключевые понятия
Многочлен. Рациональная дробь. Иррациональная функция. Тригонометрическая функция.
-
Интегрирование выражений, содержащих квадратный трехчлен
Пусть подынтегральная
функция содержит квадратный трехчлен
.
-
Интегралы вида
вычисляются следующим образом. Из
квадратного трехчлена в знаменателе
выделим полный квадрат:
где
,
если
и
,
если
.
Далее сделаем
подстановку
,
откуда
,
.
Получим
.
Последний интеграл является табличным и вычисляется по формулам 15, 16 таблицы основных неопределенных интегралов.
Пример
1.
Вычислить интеграл
.
Решение. Выделим в знаменателе полный квадрат:
.
Сделаем подстановку
.
Тогда
и
.
Возвращаясь к переменной х, получим
.
-
Интегралы вида
вычисляются аналогично интегралам
пункта 1
путем выделения полного квадрата из
квадратного трехчлена и последующей
замены переменной. В результате исходный
интеграл сводится к одному из табличных
интегралов вида 12, 13.
Пример
2.
Вычислить интеграл
.
Решение.
Преобразуем
квадратный трехчлен следующим образом:
.
Получим
.
Положим
,
тогда
,
.
В результате получаем
=
.
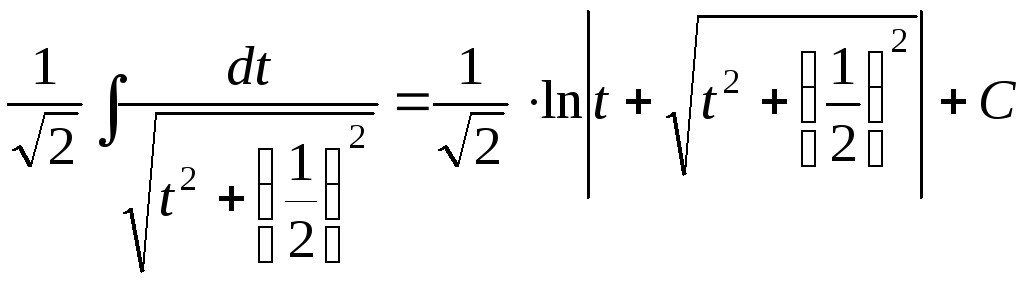Переходя к переменной х,
получим
.
-
Интегралы вида
и
вычисляются путем выделения полного
квадрата из квадратного трехчлена и
последующей замены переменной. Затем
полученный интеграл разбивается на
два: первый из этих интегралов можно
вычислить, воспользовавшись формулами
(2), (3), а второй интеграл является
табличным.
Пример
3.
Вычислить интеграл
.
Решение.
Так как
,
то по-ложим
.
Тогда
и
= [полученный интеграл разобьем
на два] =
.
Второй из этих
ин-тегралов
– табличный:
.
Для нахождения первого
воспользуемся следующим преобразованием
дифференциала:
.
В результате получим
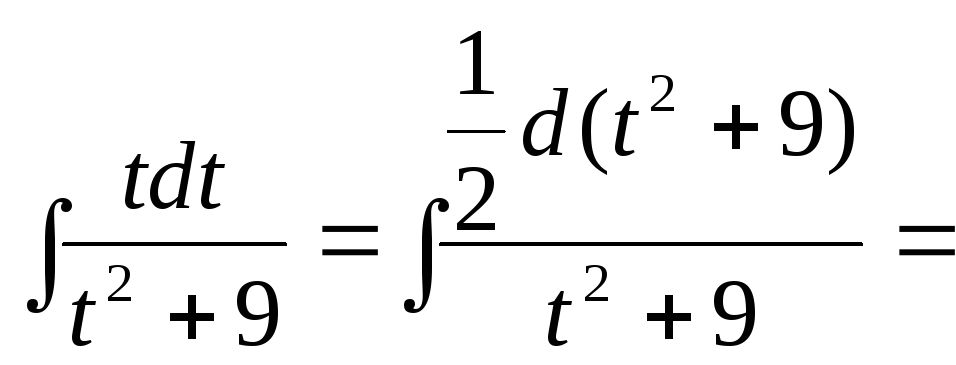
= [воспользуемся
формулой (3)] =
.
Окончательно имеем
,
где
.
Возвращаясь к переменной х,
получим
.
-
Интегрирование простейших рациональных дробей
Определение.
Рациональной
дробью называется дробь вида
,
где
и
– многочлены степени
и
соответственно.
Рациональная дробь
называется правильной,
если степень числителя меньше степени
знаменателя, т.е.
,
и неправильной
– в противном случае (
).
Простейшей рациональной дробью называется правильная дробь одного из следующих видов:
1)
;
2)
;
3)
;
4)
.
Интегралы от рациональных дробей 1), 2) находятся методом замены переменной:
[положим
тогда
]
=
[возвращаемся
к переменной x]
=
;
[
]
=
[возвращаемся
к переменной x]
=
.
Пример
4.
Вычислить интеграл
.
Решение.
[
сделаем замену
] =
.
Интегралы от
рациональных дробей 3), 4) вычисляются
аналогично интегралам
,
рассмотренным в п. 1.