Занятие 4
Тема: ОПЕРАЦИИ НАД ТЕНЗОРАМИ
п.1. Связь между компонентами тензора с различными строениями индексов.
Задача 1. Показать, что если
компоненты метрического тензора, то
компоненты тензора
преобразуются в компоненты со смешанным
строением индексов по формуле:
Решение. Покажем, что с лева и с права стоят компоненты одного и того же тензора. Образуем линейные комбинации:
1)
=
Поэтому, если
верно, то должны получить тот же тензор
2)
=
=
=
=
Требуемое показано. Задача 1 – пример «жонглирования» индексами.
Задача 2. Матрица компонент
тензора 2-го ранга имеет вид:
,
метрическая матрица (
)
равна
.
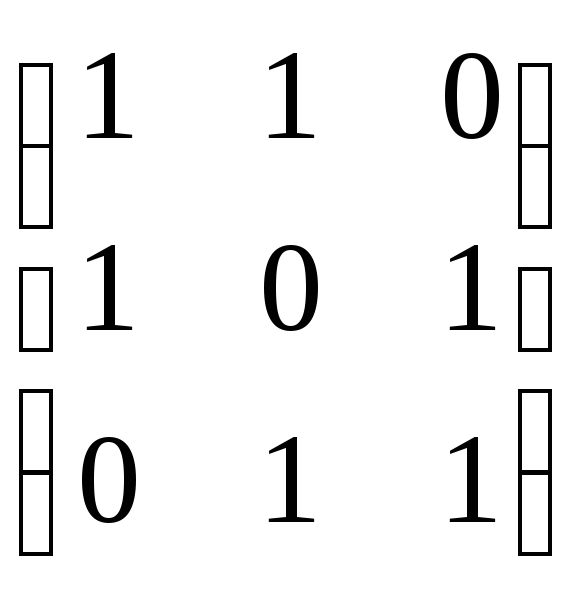Определить матрицу компонент
.
Решение. Осуществив «жонглирования» индексами, имеем
Порядок индексов матрицы (
)
несущественен. В результате произведения
матриц находим искомую:
=
=(
)
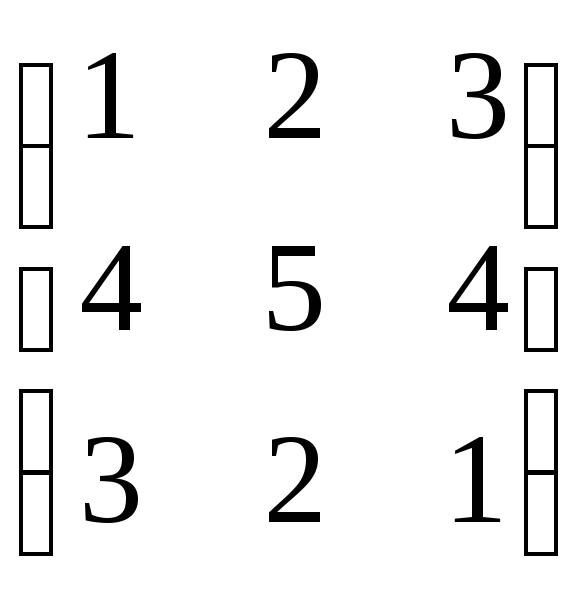
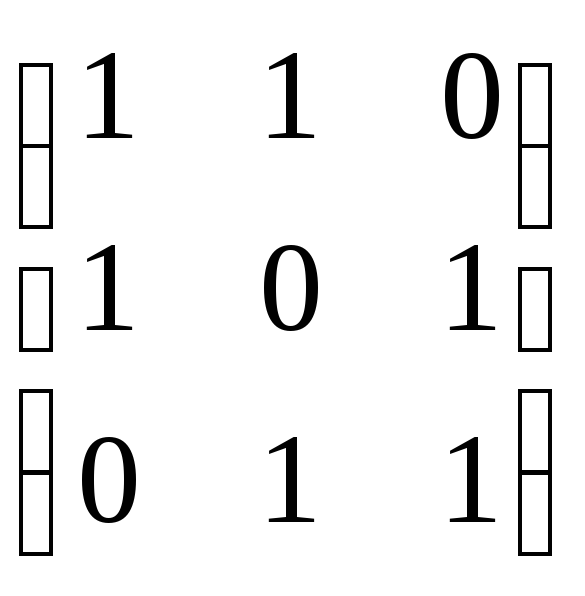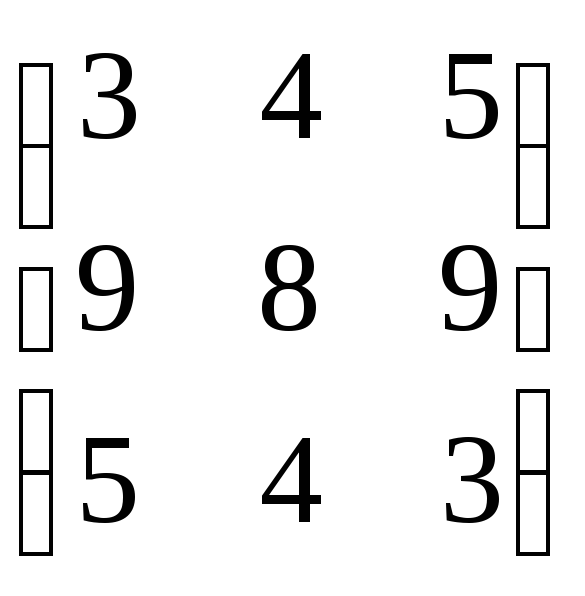Матрица определяет компоненты тензора
в базисе
Задача 3. Представить все формы записи тензоров 3-го ранга, используя тензорные произведения 3-х базисных векторов.
Решение.
=
=
=
=
=
=
=
=
.
п.2. Тензорное (внешнее) произведение тензоров есть тензор, ранг которого равен сумме рангов сомножителей, а компоненты произведению компонент сомножителей. В частном случае диада - тензорное произведение двух векторов.
Пусть
=
,
.
Тензорное произведение
=
-
тензор 5-го ранга.
Задача 4. Представить различные
формы записи тензорного произведения
вектора
и тензора второго ранга
Решение.
=
=
=
=
=
=
=
=
=
.
п.3. Сложение тензоров определяется только для тензоров одной валентности; компоненты суммы определяются как сумма компонент слагаемых с одинаковым строением индексов.
Задача 5. Показать, что если
и
компоненты тензора, то комплекс
+
не компонента тензора.
Решение. Используя правила преобразования компонент тензора. Получим
+
=
+
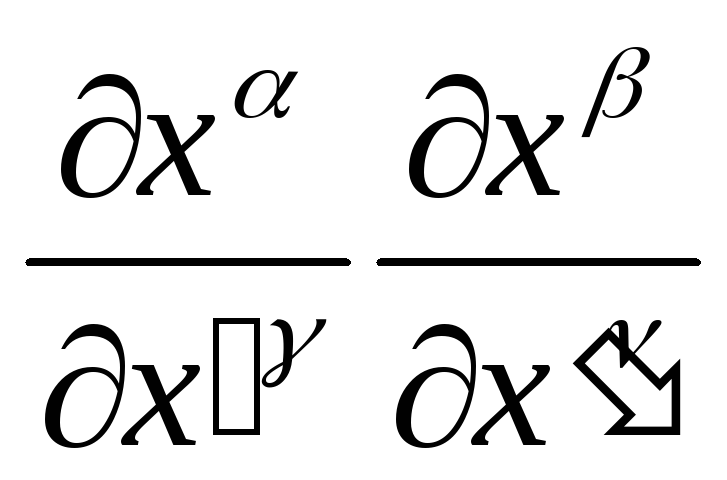
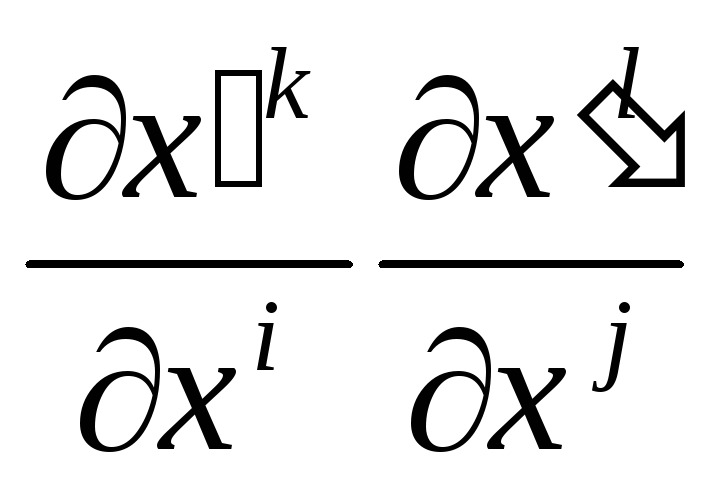
-это противоречит правилу преобразования компонент тензора.
п.4. Скалярное произведение тензоров вычисляется следующим образом:
=
=
(
)
=
=
=
.
Скалярное произведение тензоров – тензор, ранг которого меньше суммы рангов сомножителей на два.
Задача 6. Доказать, что
=
,
где
=
.
Решение.
=
=
=
=
п.5. Двойное скалярное произведение вычисляется следующим образом:
:
=
:
=
(
)(
)=
=
Следом тензора называют двойное скалярное произведение тензора и метрического тензора. Обозначение следа:
Sp
=
tr
=
:
.
Дополнительные задачи:
-
Найти выражение следа тензора второго ранга через его компоненты.
-
Записать различные формы представления скалярного произведения 2-х тензоров 2-го ранга.
-
Доказать, что
=
=
-
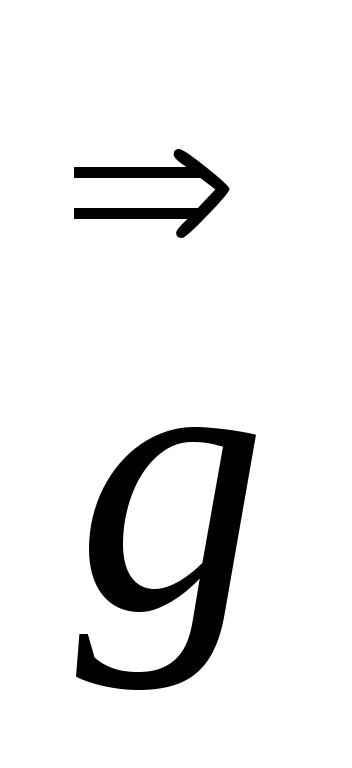
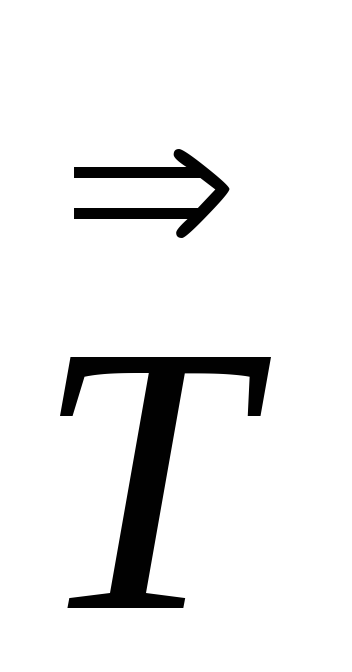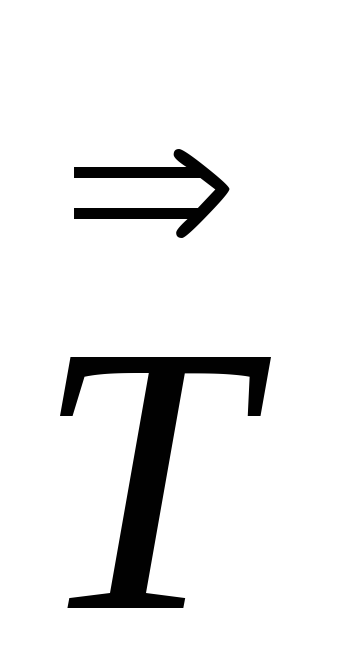
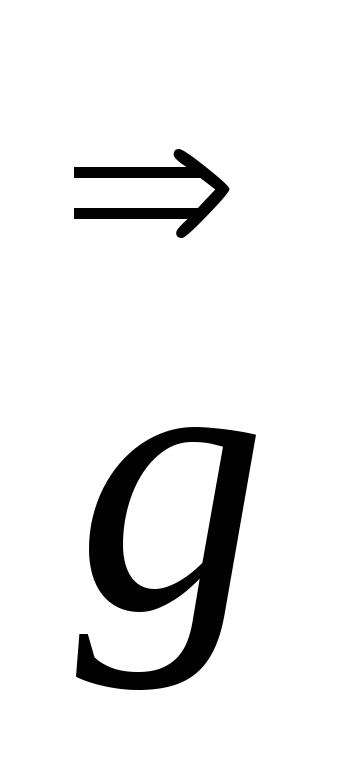По определению степени тензора
=
,
=
,
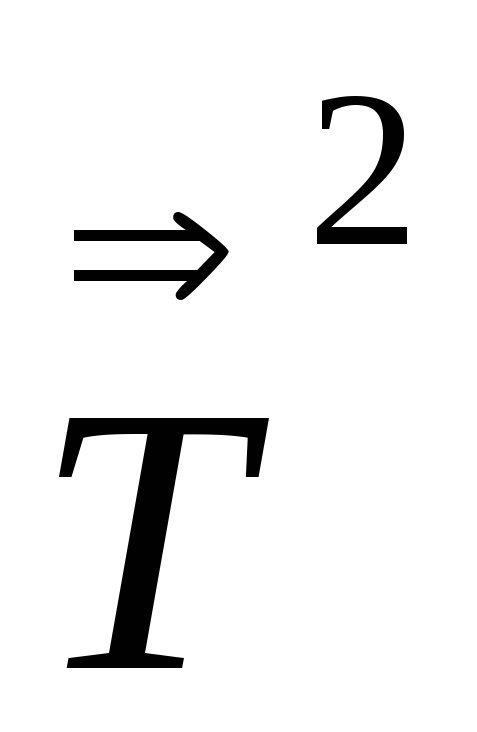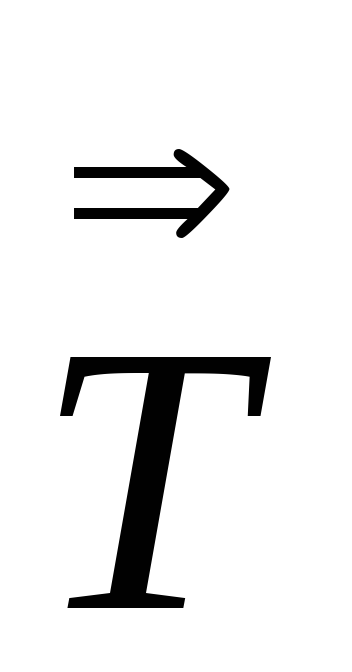
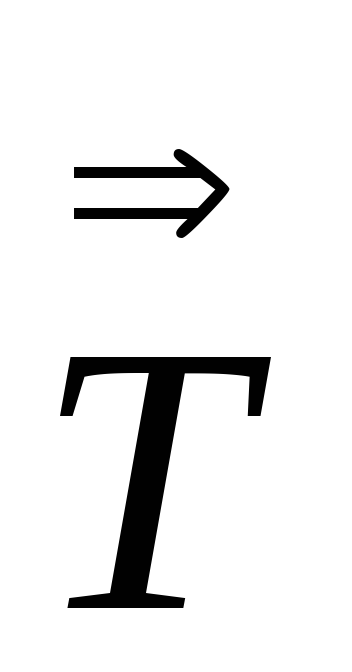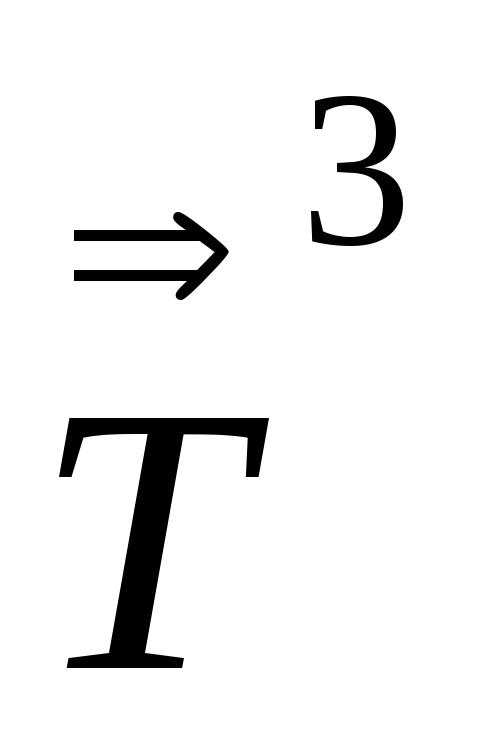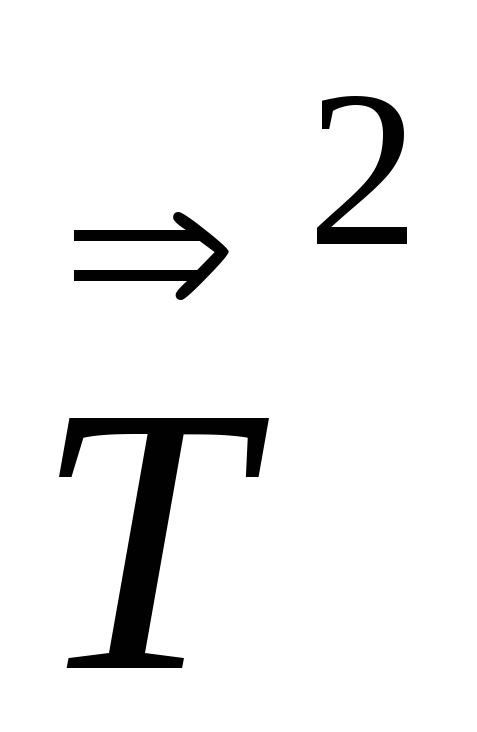
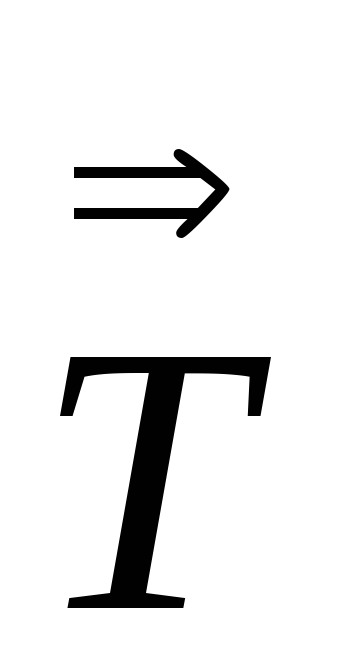Выразить компоненты
,
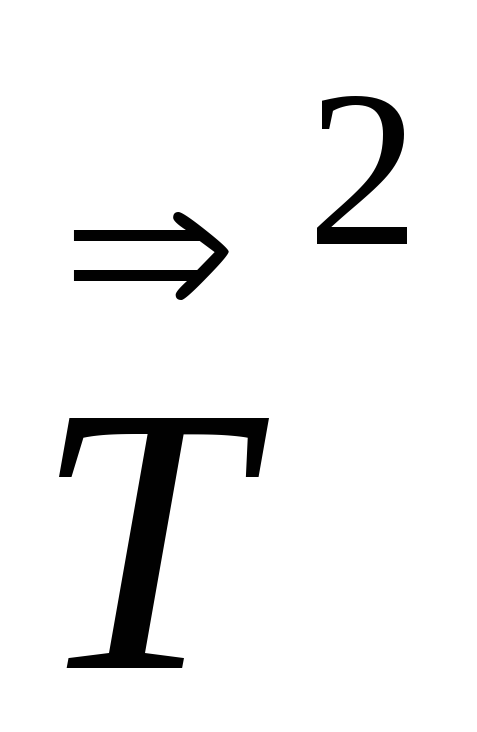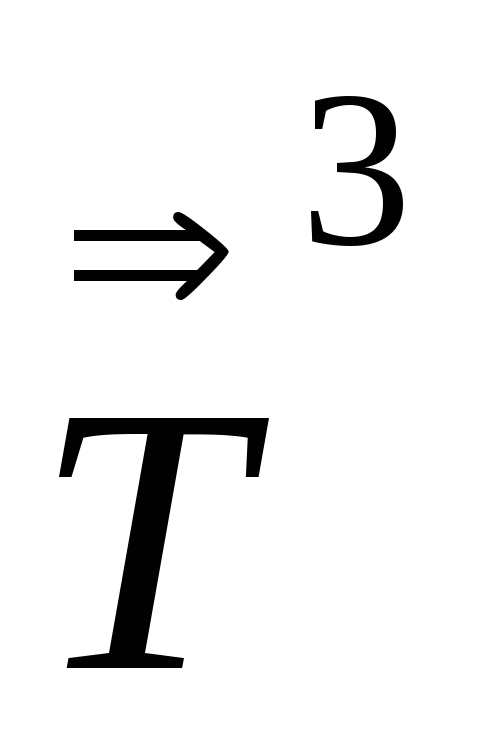через компоненты тензора
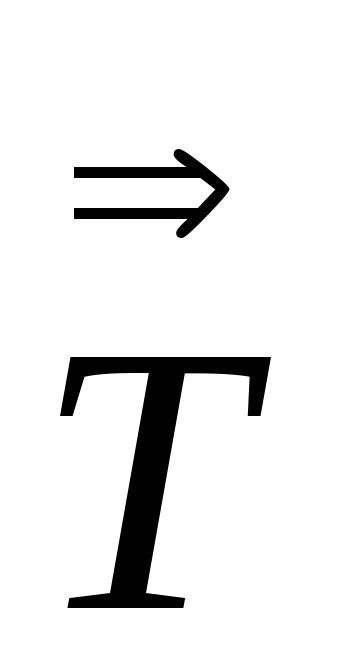второго ранга. -
Вычислить
:
,
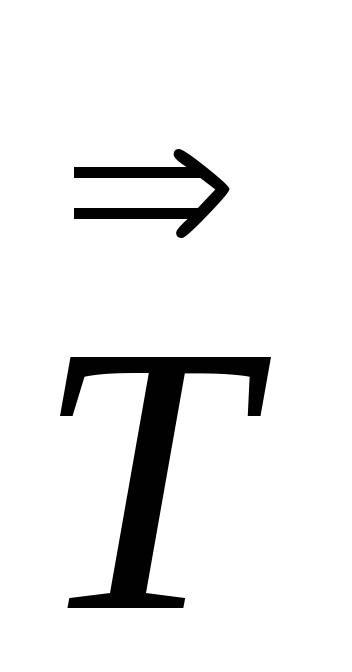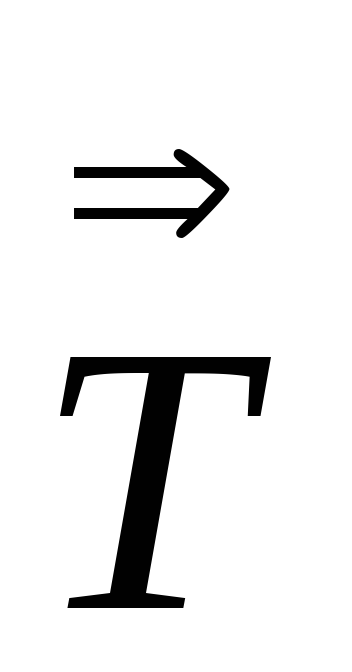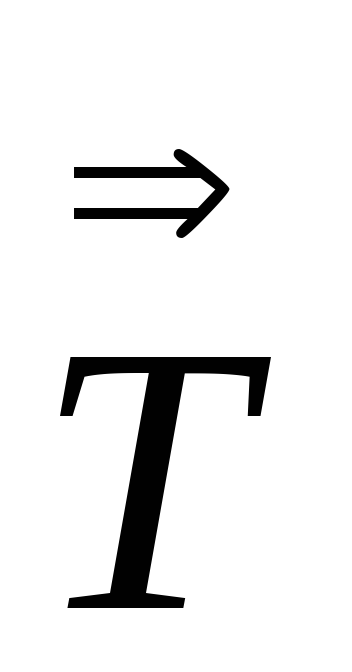- тензор 2-го ранга. -
Доказать, что
:
=
:
-
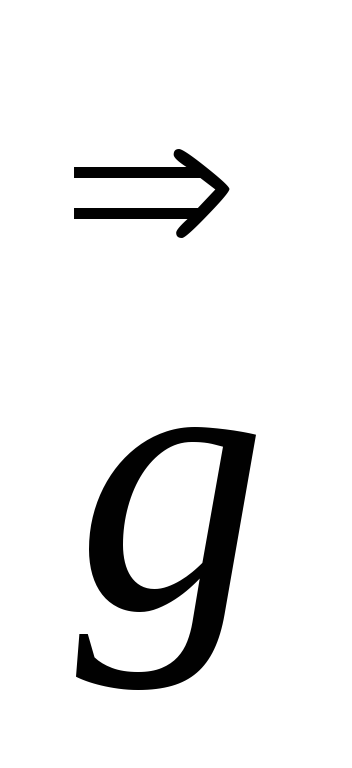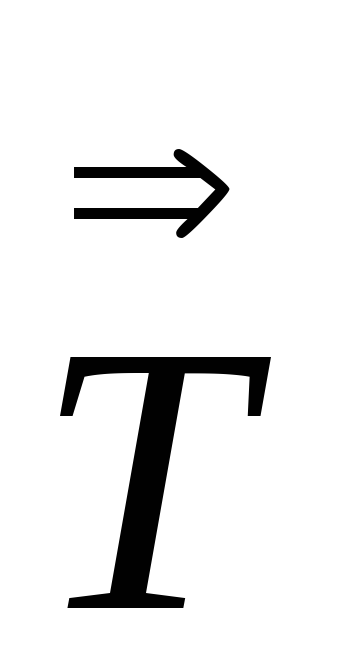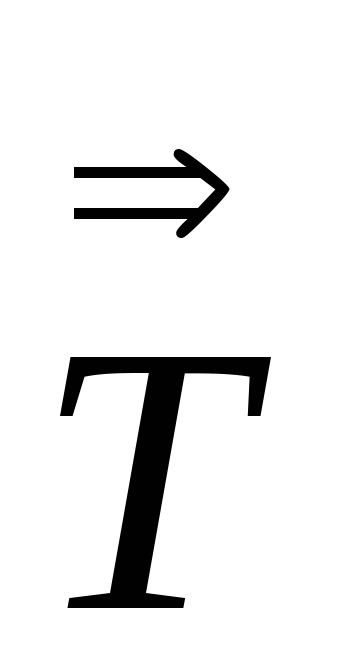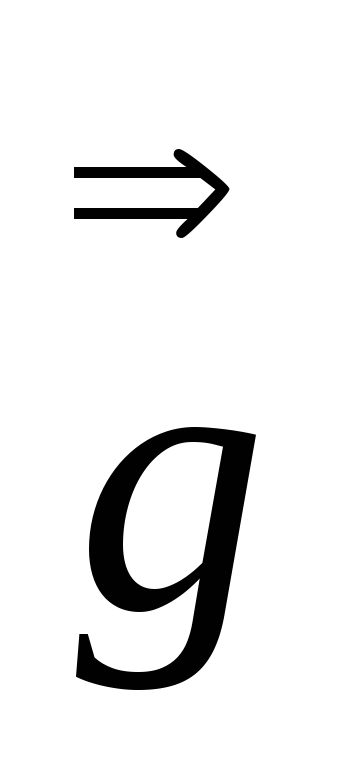
Вычислить 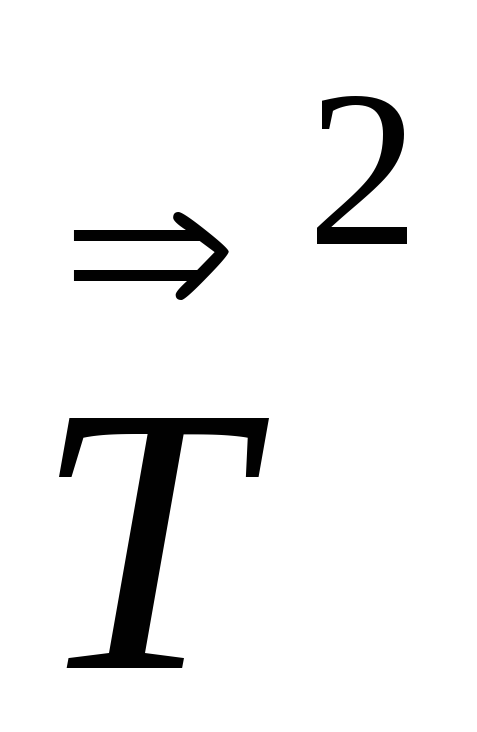Sp
,
Sp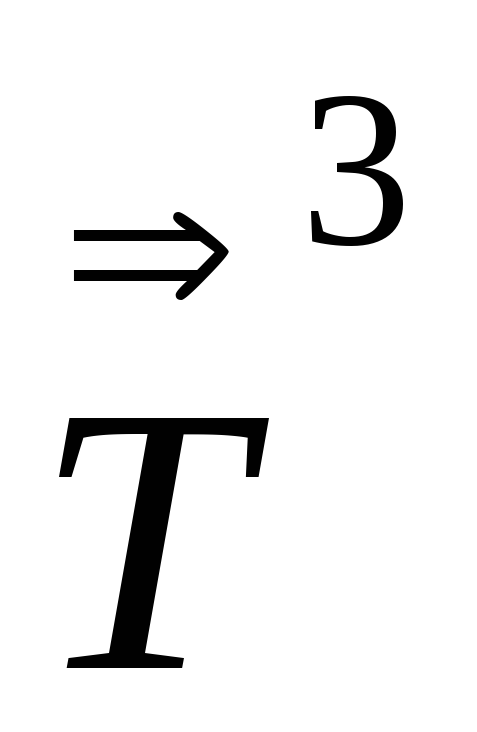
,
тензор 2-го ранга.
Решение.
-
Sp
=
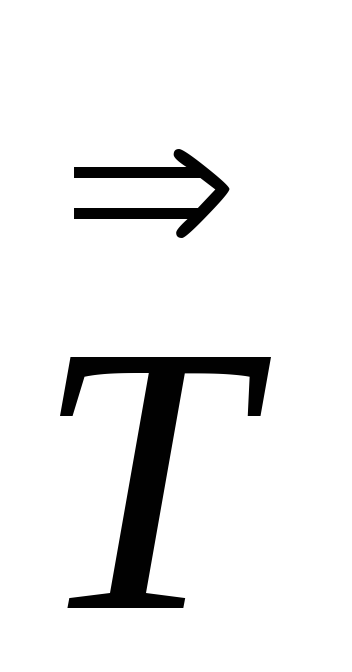tr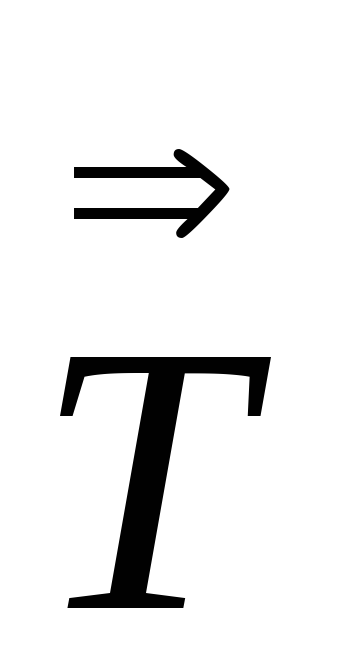
=
:
=
=
. -
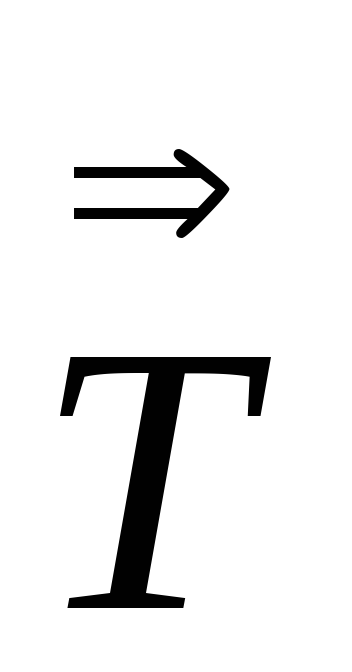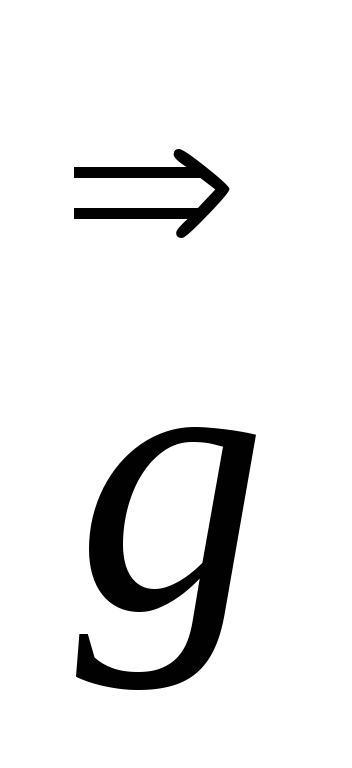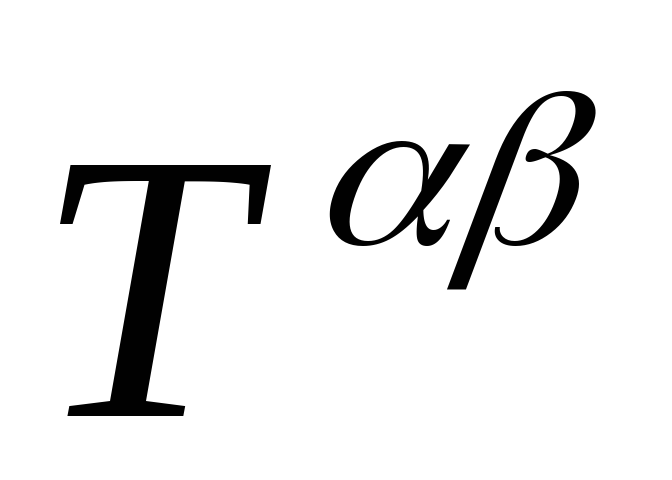
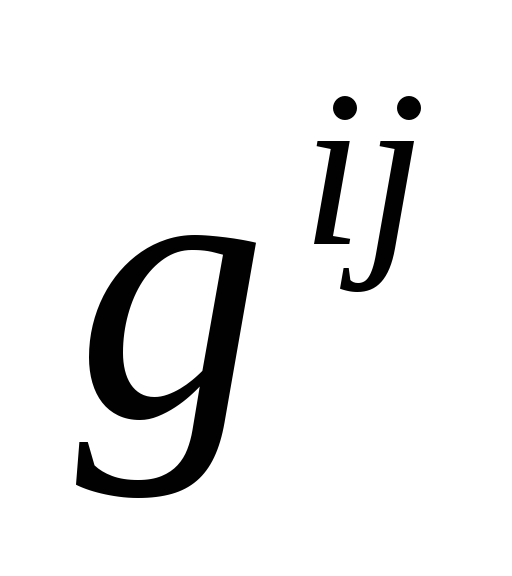
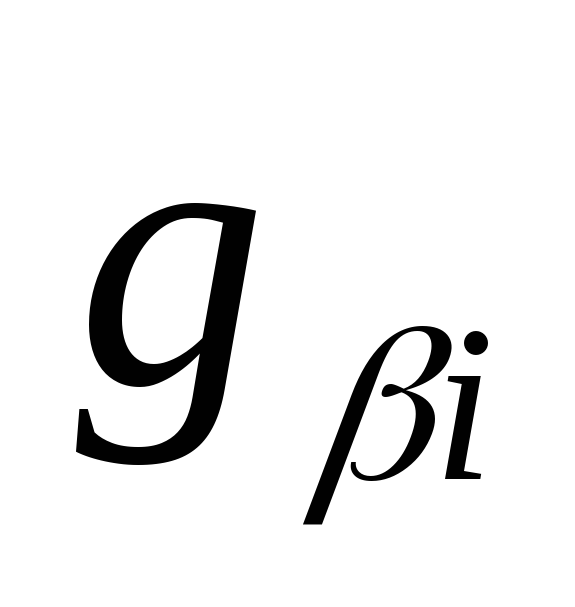
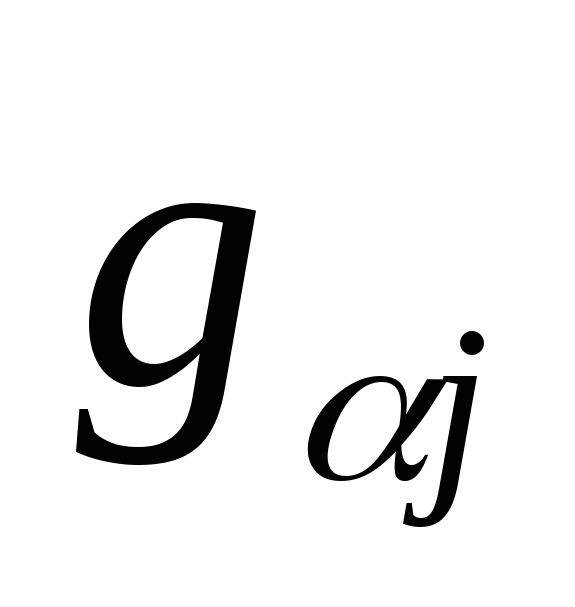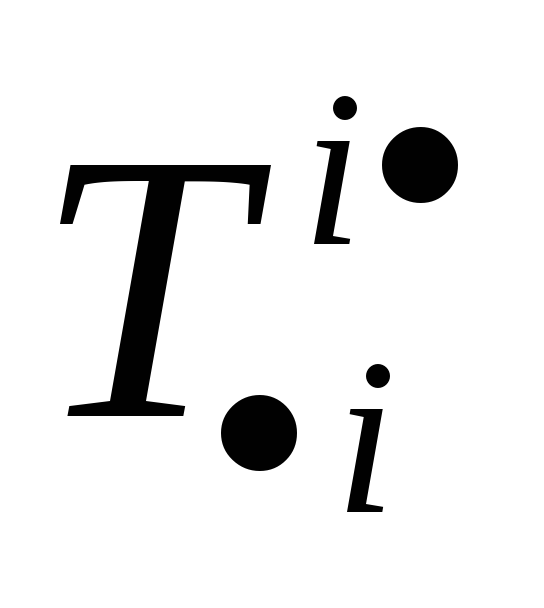Аналогично п.3.
-
Аналогично Задаче 6, доказываем
=
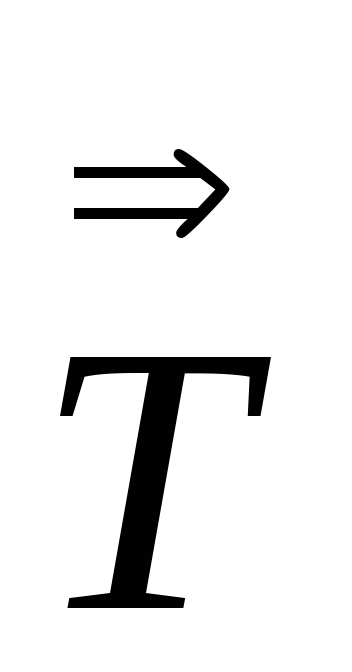
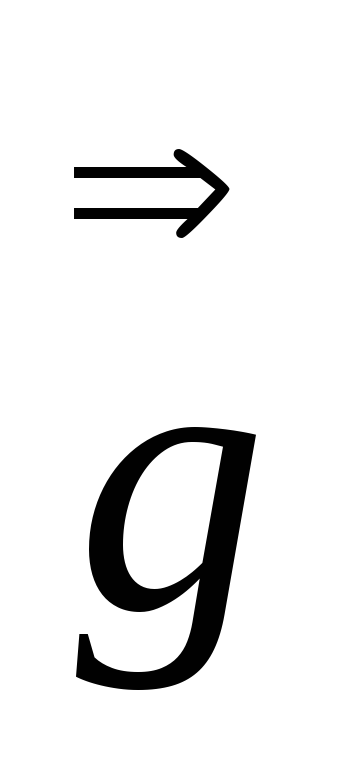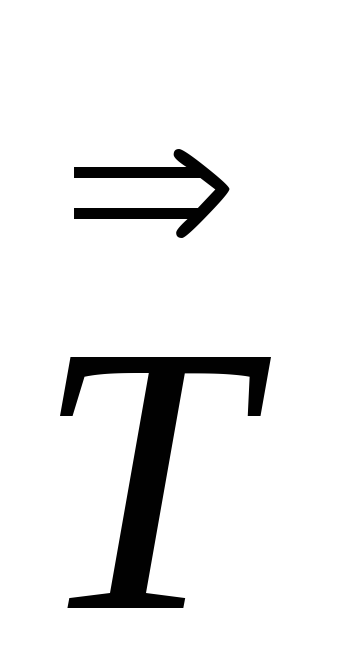и следовательно
=
=
. -
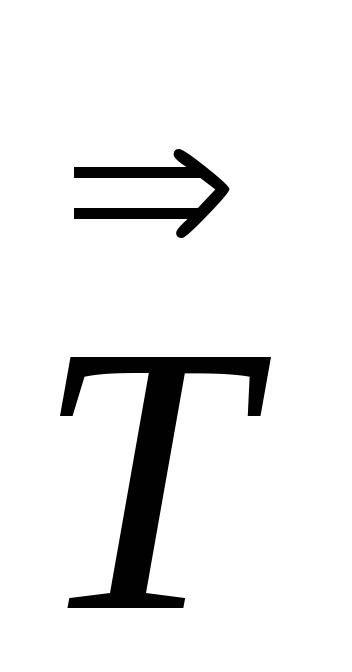
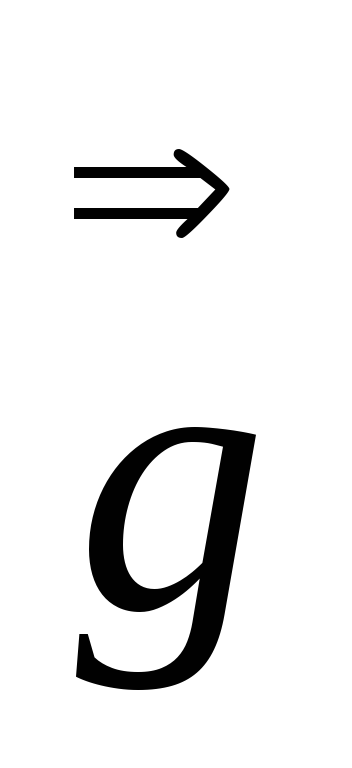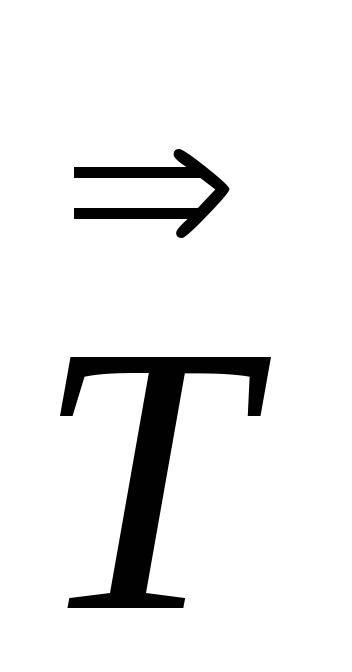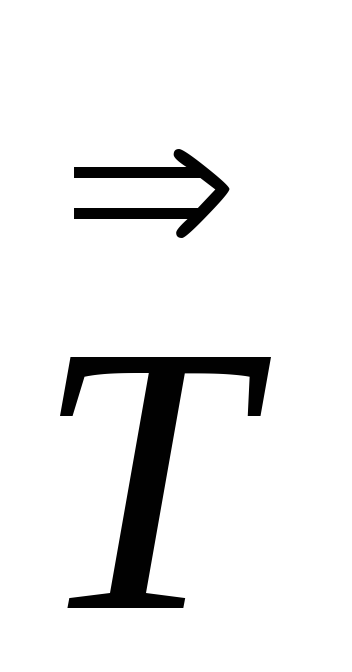Так как
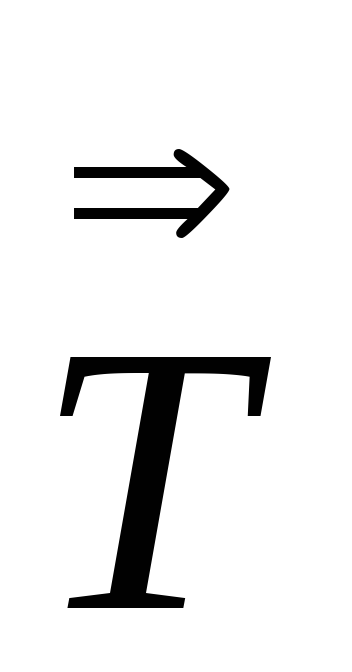тензор второго ранга, следовательно,
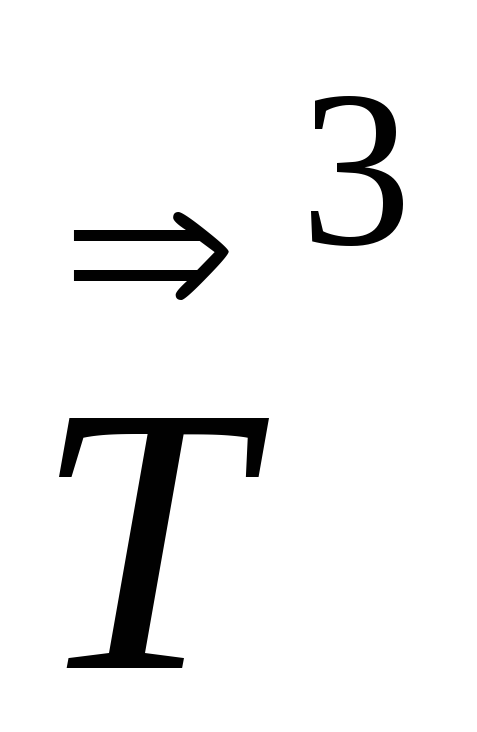-тензор
второго ранга, аналогично дополнительной
задаче 2. -
Аналогично
:
,
:
=
(
)(
)=…
-
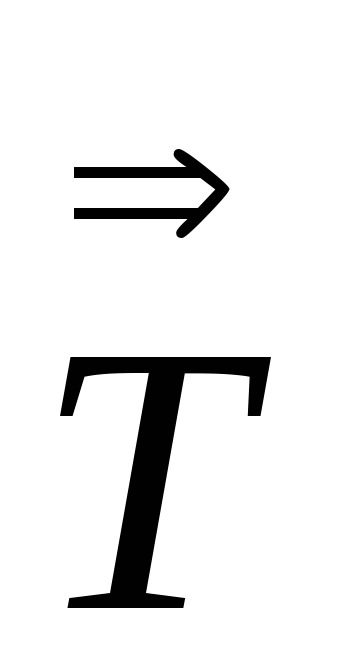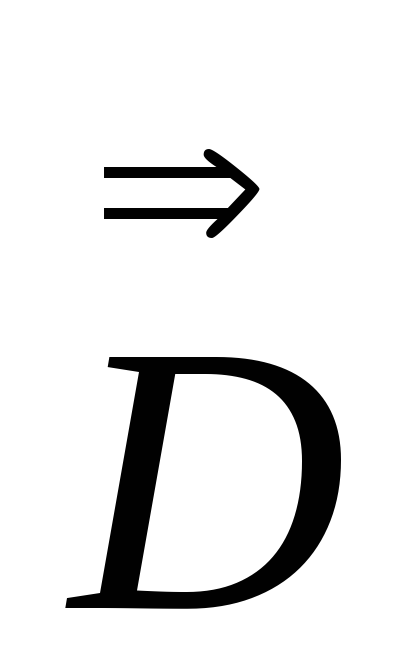Воспользуемся определением следа тензора Sp
=
:
. -
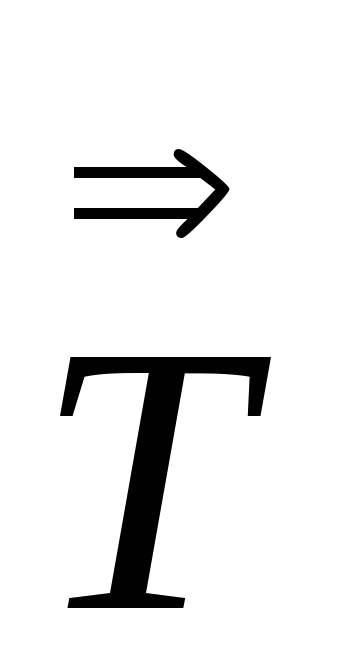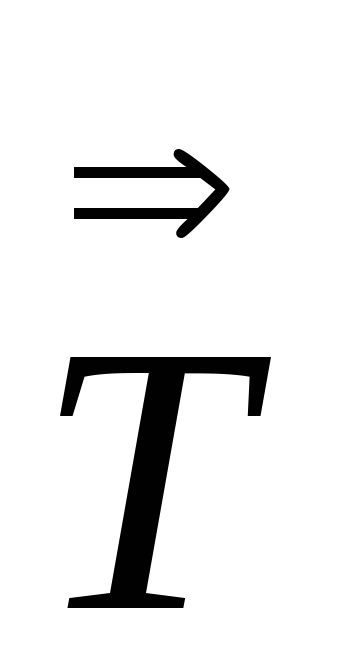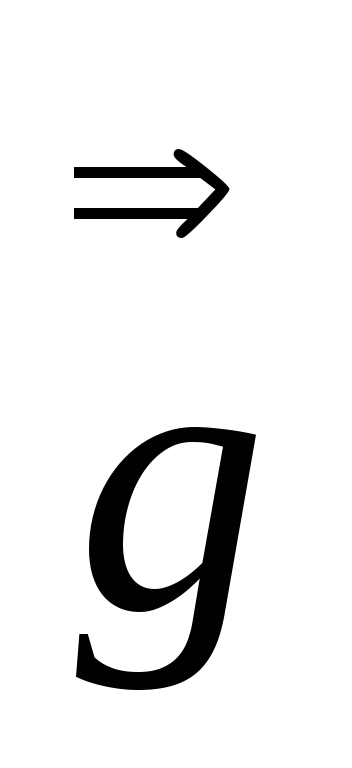Так как
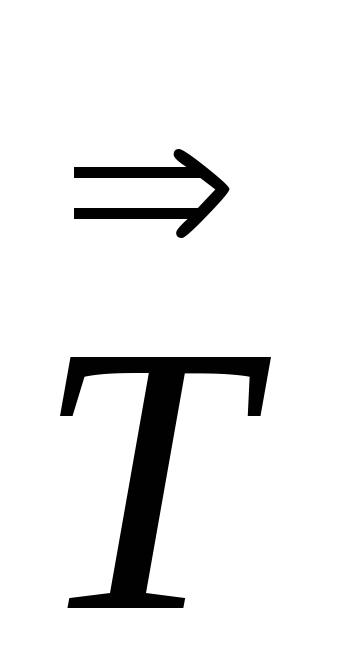тензор второго ранга, следовательно,
,
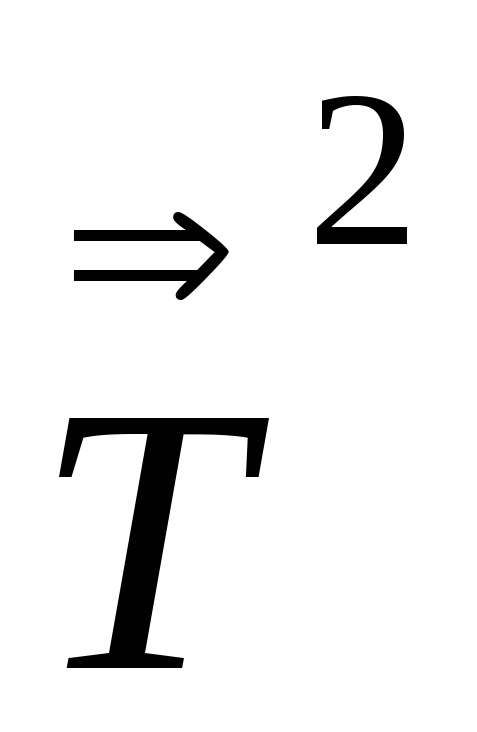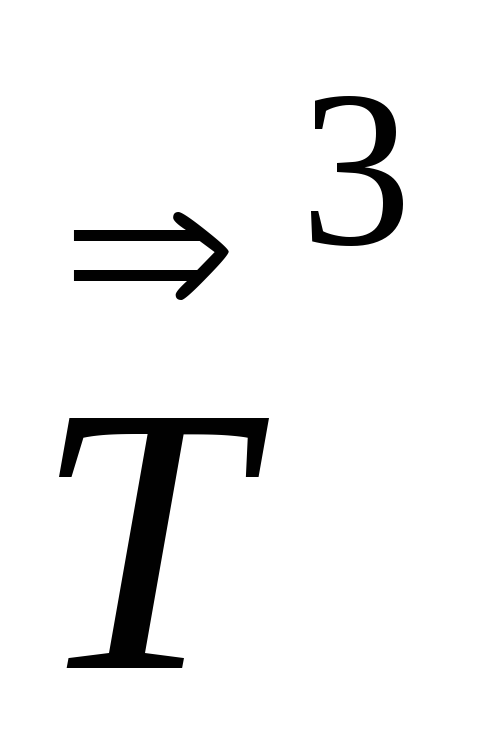-тензора
второго ранга. Используя дополнительное
задание 4 и определение Sp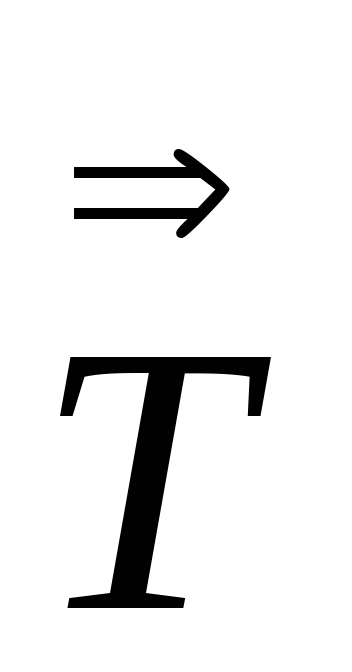
находится 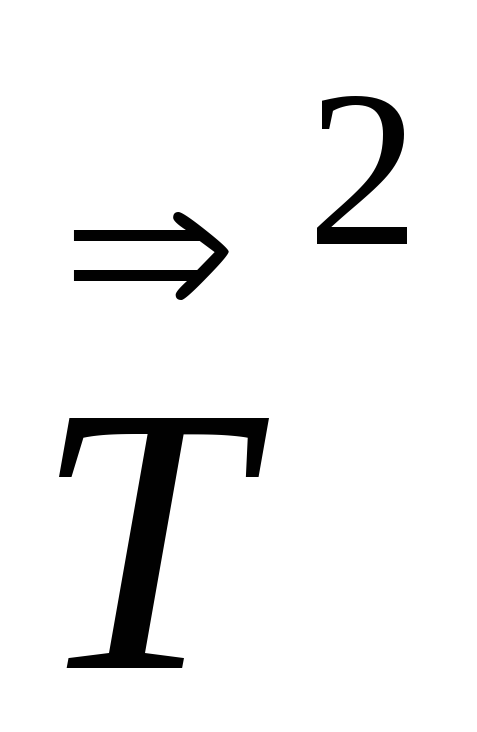Sp
,
Sp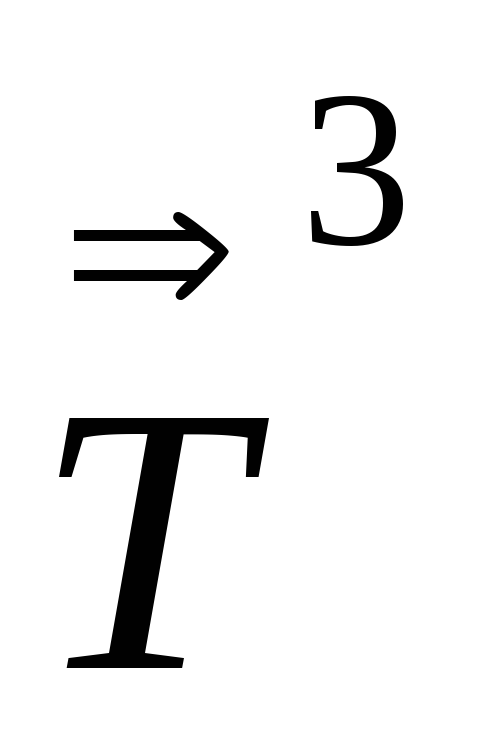
.
План занятия.
8 минут – проверка домашнего задания
Решение задач у доски:
Пояснение п.1 (2 минут)
Пояснение п.2 (2 минут)
задача 1 (10 минут)
задача 3 (5 минут)
Пояснение п.2 (2 минут)
задача 4 (5 минут)
Пояснение п.3 (1 минут)
задача 5 (5 минут)
Пояснение п.4 (2 минут)
задача 6 (5 минут)
Пояснение п.5 (3 минут)
Решение дополнительных задач:
задача 1 (10 минут)
задача 2 (10 минут)
задача 4 (10 минут)
Домашнее задание:
задача 2
Дополнительные задачи 3,5,6,7.
Занятие 5
Тема: СВЕРТКА. АЛЬТЕРНИРОВАНИЕ И СИММЕТРИРОВАНИЕ,ТЕНЗОРНАЯ
ПОВЕРХНОСТЬ. ГЛАВНЫЕ ЗНАЧЕНИЯ И ГЛАВНЫЕ НАПРАВЛЕНИЯ СИММЕТ-РИЧНОГО ТЕНЗОРА 2-го РАНГА
п. 1. Обсуждение дополнительных задач Занятия 4 Решение.
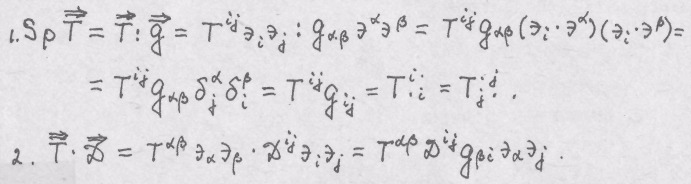
Осуществляя "жонглирование" индексами, получим:
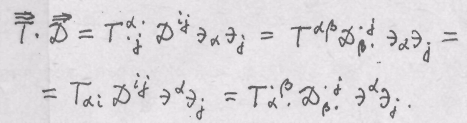
3.
Метрический тензор выполняет роль
своеобразной"единицы":
Действительно,
(см.также задачу 6 занятия 4).
4. Вычисление компонент квадрата и куба тензора 2-го ранга требуется для нахождения его инвариантов. Имеем:
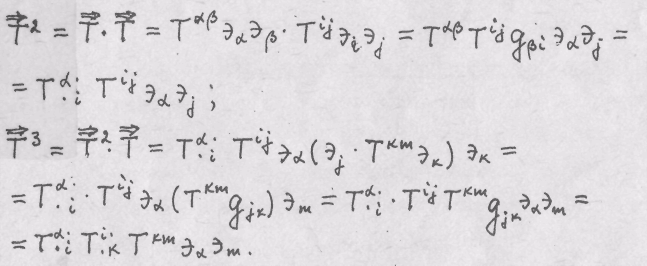
Степени тензора 2-го ранга-тензора того же ранга.
5. Если
- тензор 2-го ранга, то
-
скаляр
(инвариант). Действительно,
б. Аналогично 5 имеем
1. Учитывая предыдущие упражнения, сразу записываем
п.2.
Свертка -
операция, выполняемая над тензором,
компоненты которого имеют по крайней
мере один но- и один контравариантный
индекс. Свертка тензора
по
и
это переход к
тензору
, по
и
- переход
к
тензору
. Свертка двух тензоров есть свертка их
тензорного
произведения. Например,
Свертка по индексам
и
дает тензор
Задача
1. Показать, что свертка тензора
по
индексам
и
равна
_Решение. По определению свертка данного
тензора есть вектор
. С другой стороны,
п.3.
Альтернирование
и симметрирование
тензора- выделение его антисимметричной
и симметричной частей. Тензор называется
симметричным (антисимметричным) по
индексам
и
, если компоненты его не меняются
(изменяют только знак) при перестановке
и
; для тензоров 2-го- ранга не имеет смысла
указывать, по каким индексам симметрия
или антисимметрия.
Тождество;
лежит в основе указанных операций для тензоров 2-го ранга.
Задача
2.
Матрица
компонент
тензора имеет вид:
Определить матрицы компонент симметричной и антисимметричной частей тензора.
Решение. Используя тождество, получим:
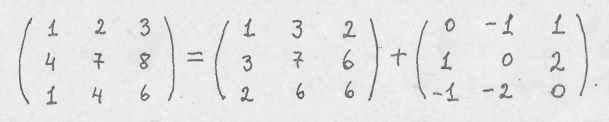
в правой части равенства находятся искомые матрицы.
Задача 3. Доказать, что свертка симметричного тензора и антисимметричного равна нулю. Рассмотреть случай тензоров 2-го ранга.
Решение.
Пусть
-симметричный,
антисимметричный
тензоры.
Свертка тензорного
произведения
по обоим индексам равна
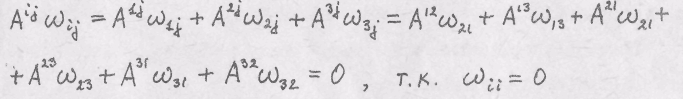
(по
нет
суммирования).
п. 4. Тензорная поверхность симметричного тензора 2-го ранга в данной точке определяется уравнением:
Квадратичная
форма
представляет собой сверт-
ку
симметричных тензоров
и
. Здесь
-
компонента бесконечного малого вектора
в данной точке.
Конец
этого вектора лежит на тензорной
поверхности - поверхности 2-гo
порядка. В осях, соответствующих главным
направлениям, уравнение поверхности
приводится к каноническому виду.
Единичный вектор
, определяющий главное направление,
удовлетворяет соотношению:
Задача 4. Показать, что контравариантные компоненты вектора удовлетворяют системе уравнений:
Решение. Имеем
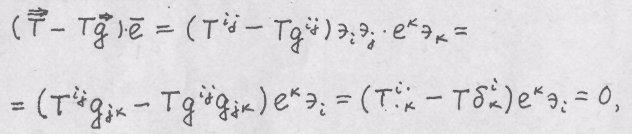
отсюда следует искомая система однородных линейных алгебраических уравнений.
Условие нетривиальности решения этой системы определяет характеристическое уравнение
Решением последнего уравнения являются главные значения тензора
. Каждому значению
соответствует свое
нетривиальное
решение системы
Компоненты
определяют три главных
направления
тензора.
Задача
5.
Найти главные значения и главные
направления тензора
в точке, матрица компонент которого
имеет виц:
Решение. Характеристическое уравнение имеет в данном случае виц:
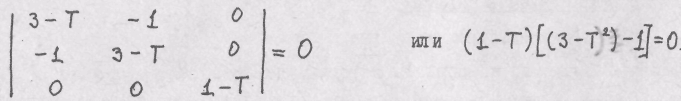
Корни
этого уравнения определяют три главных
значения
,
Компоненты
, соответствую-
щие
,
определяются из системы;
Первые два уравнения имеют лишь тривиальное ранение, так как детерминант этой однородной системы отличен от нуля (равен 3):
Компоненты
, соответствующие
, опреде-
ляются из системы:
Получаем
,
. Компоненты
соответствующие
,
определяются
из системы;
Получаем
Если
определен компонентами
в декартовой систе-
ме
координат, а вектор
единичный, то
Вектора
главных направлений имеют следующее
разложение по направлениям ортов
:
Дополнительные задачи.
1. Установить, го каким индексам симметричны или антисим -метричны тензоры, компоненты которых удовлетворяют условиям
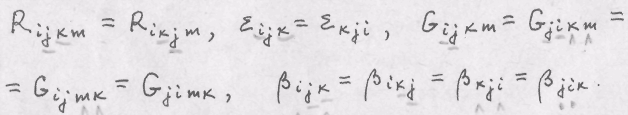
2.
Доказать,
что если тензор с компонентами
сим-
метричен
по индексам
и
, антисимметричен по
и
,
то он равен нулю.
3.Зная
матрицу
(см.задачу 5), вычислить
(ответ 3; 21; 73). 4.
Характеристическое уравнение можно
представить в форме:
где
- скалярные инварианты тензора 2-го
ранга, имеющие
представления;
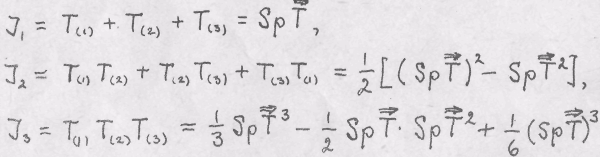
Зная
матрицу
(см.задачу 5), проверить справедливость
этих представлений.
5. Показать, что след антисимметричной части тензора 2-го ранга равен нулю.
6. Найти главные значения и главные направления
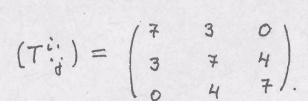
З а н я т и е 6 Тема. ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА И ТЕНЗОРА ПО КООРДИНАТЕ
В общем случае при переходе от точки к точке изменяются и компоненты вектора (тензора), и величины, и направления базисных векторов.
Задача
1.
Исходя из введения коэффициентов
связности
в равенстве
,
доказать формулу дифферен-
цирования
вектора
по координате:
Решение.
Дифференцируем инвариантные представления
вектора
. Имеем:
переобозначая
во втором слагаемом немые индексы
(вместо
берем
, вместо
берем
), получаем искомое.
Задача 2. Доказать формулу представления ковариантной производной от ковариантной компоненты вектора
Решение.
Пусть
.
Тогда
Разложим
в том же ба8исе, что и
Коэффициенты
выражаются черев коэффициенты связности.
Продифференцируем
скалярное произведение
.
С
другой
стороны,
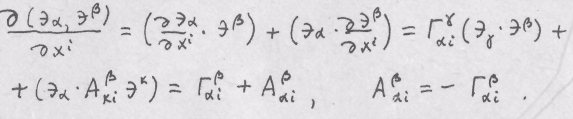
В итоге
где
Задача
3.
Показать, что
, где
-
контрава-
риантная компонента вектора есть компонента тензора.
Решение.
Образуем свертку по
:
В новой системе координат левая часть
равенства равна:
т.е.
представление остается инвариантным
и одновременно раскладываемым в
базисе
.
Следовательно,
компоненты тензора.
Задача
4.
Исходя из определения коэффициентов
связности (см.задачу 1), вывести формулу
дифференцирования компоненты тензора
2-го ранга, контравариантной по индексам,
по координате
Решение.
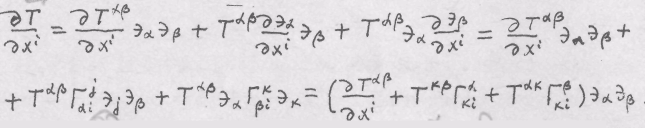
Коэффициенты связности выражаются черев компоненты метрического тензора и их производные:
. I
Задача 5. Доказать эту формулу.
Решение. Запишем выражение производных от скалярных функций.
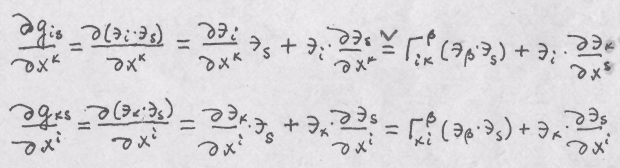
В
эвклидовом пространстве можно ввести
вектор
, поэтому
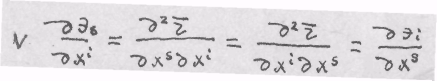
В
римановом
пространстве
, Складывая выражение
производных, получим:
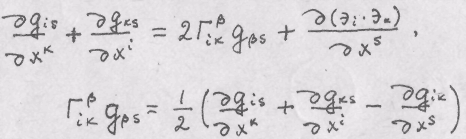
Далее,
доумножая левую и правую части на
и образуя сверт-
ку по
(неверно: сокращая на
), получим искомую
формулу.
Задача
б.
Зная компоненты матриц
и
,
найти
выражения коэффициентов
в случае сферической си-
стемы координат.
Решение. В данном случае
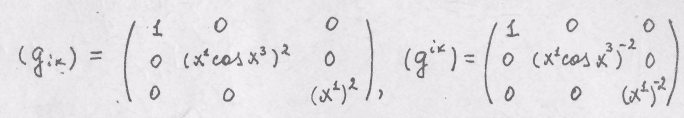
Обе
матрицы с нулевыми недиагональными
членами, с компонентами, не зависящими
от
. Поэтому
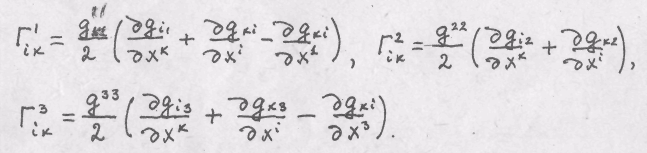
Присваиваем
Ответ.
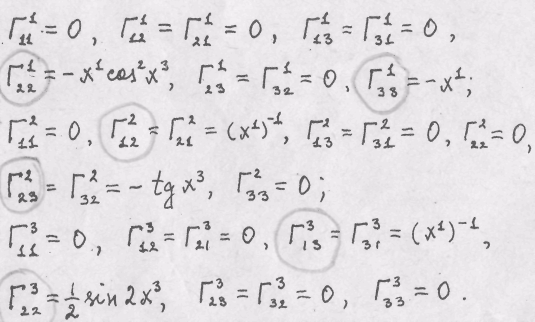
Дополнительные задачи.
1. Найти выражение ковариантной производной от компоненты тензора 2-го ранга со смешанным строением индексов.
2.
Доказать формулу:
3. Доказать формулу:
4. Найти
в цилиндрической системе координат.
5.
Вычислить ковариантные производные от
компонент вектора в сферической системе
координат:
3 а н я т и е 7.
Тема: ОСНОВНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ (ГРАДИЕНТ, ДИВЕРГЕНЦИЯ). ФИЗИЧЕСКИЕ КОМПОНЕНТЫ ВЕКТОРА
Представление
дифференциальных операторов осуществляется
с помощью символического оператора
Гамильтона
(набла), где
- обозначение
ковариантной производной. п.1.
Оператор "градиент"
( ),
Последнее
выражение - полиадное произведение.
Задача
1.
Пусть
- скалярная функция
координат.
Показать, что
- вектор, и определить его
компоненты.
Решение.
- ковариантные
компоненты вектора
Задача
2.
Найти компоненты
в декартовой
системе
координат
; здесь
Ответ.
Задача
3.
Тот же вопрос в случае сферической
системы координат
Решение.
Так как
скалярная функция, то ковариантная
производная
от
совпадает с частной, при
ковариантные компоненты имеют вид:
п.2.
Оператор
"дивергенция"
Применяется
к тензорным величинам ранга больше
нуля. Задача
4.
Выразить
- вектор, в декартовых
координатах.
Решение.
В указанных координатах коэффициенты связности равны нулю, поэтому
Задача
5.
Выразить
,
- вектор, в случае
произвольной системы координат. Решение.
Сумма
коэффициентов
вычисляется по формуле
Вейла: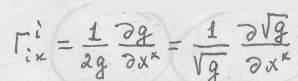
где
Задача 6. Проверить формулу Вейла в случае ортогональной системы координат.
Решение. В указанном случае имеем:
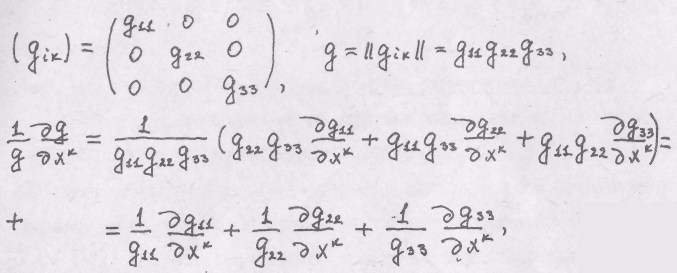
но в случае ортогональной системы(суммирования
по
нет).
Поэтому
Но
в случае той же системы равно
Требуемое
показано.
Задача
7.
Доказать формулу; компоненты вектора.
Решение.
"Немые"
"индексы можно обозначить любыми
буквами, переобозначим все черев
,
получим искомое.
Задача
8.
Выразить
через переменные
сферической система координат.
Решение.
В
случае
указанной системы
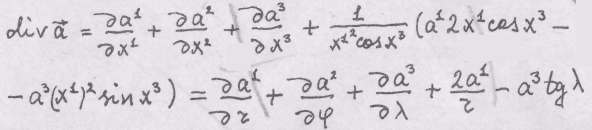
п.3.
Физические компоненты вектора
в точке
.
равны
ортогональным
проекциям вектора на направление
касательных к координатным линиям,
проходящим через заданную точку. Термин
применяется линь в случае ортогональной
системы координат. Физические
компоненты, вообще говоря, отличны от
контравариантных
, их связь определяется выражением:
(суммирования
по
в правой части нет).
Задача 9. Вывести формулу связи физических и контравариантных компонент вектора.
Решение.
- орта, направленные по
базисным
векторам
ортогональной системы координат.
Так как
(сумииров.
по
нет). Физические компоненты векторов в
сфе-
рической системе координат обозначают
Задача
10.
Выразить
через физические ком-
поненты
вектора
сферической системы координат.
Решение. В рассматриваемом случае
поэтому
Дополнительные задачи.
1.
Записать оператор
черев физические компо-
ненты
вектора
в цилиндрической системе координат.
2.
Записать
физические компоненты
в сфери -
ческой системе координат.
Занятие 8
Тема. ОСНОВНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ (ЛАПЛАСИАН, РОТОР, МАТЕРИАЛЬНОГО ДИФФЕРЕНЦИРОВАНИЯ ПО ВРЕМЕНИ )
П.1.
Лапласиан.
.
Задача
1. Записать
выражение
,
где
– скалярная функция, в ортогональной
криволинейной системе.
Решение.
По определению
.
Контравариантная компонента
связана с ковариантной соотношением:
или в ортогональной системе координат
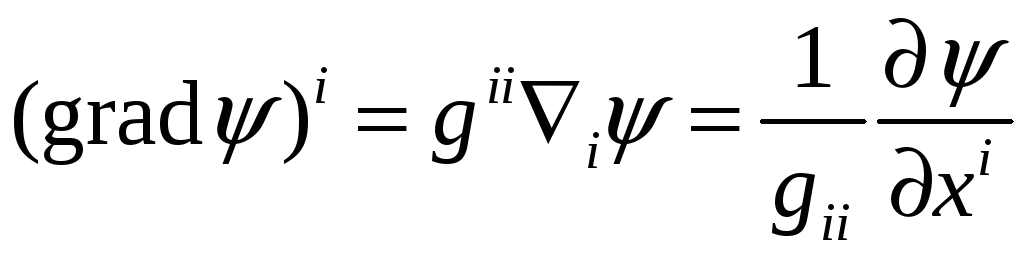
(суммирования по
нет). Используя формулу Вейла при
представлении дивергенции, получаем:
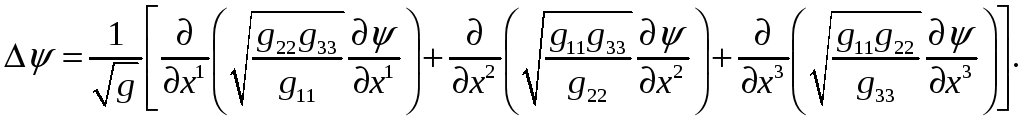
Задача 2. Записать выражение лапласиана в сферической системе координат (рис. 1).
Решение.
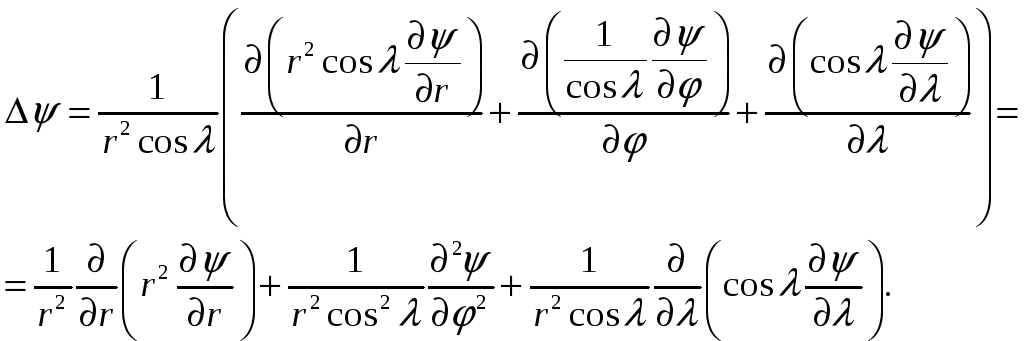
П.2.
Векторное произведение
векторов
и
есть псевдовектор
.
,
где
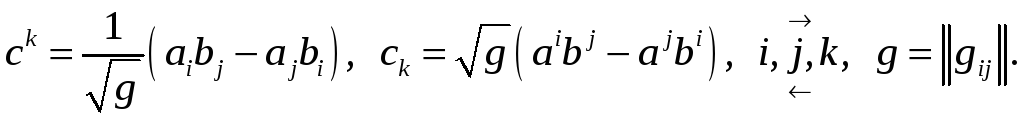
Запись компонентов
упрощается с введением псевдотензора
Леви-Чивиты, компоненты которого равны:
Задача 3. Показать справедливость представления :
Решение.
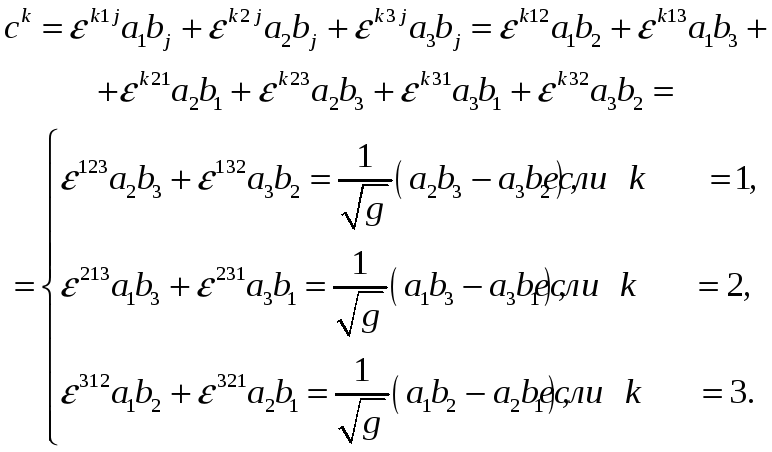
Что требовалось показать.
В декартовой
системе координат
,
соответственно
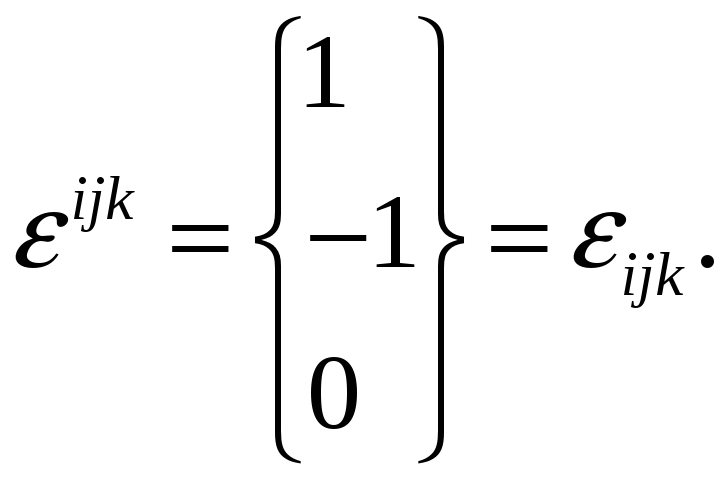
Задача 4.
Записать компоненты вектора
в декартовой системе координат.
Ответ.
Выражения получаются
друг из друга циклической перестановкой
индексов
.
П.3. Оператор
«ротор ( )»,
.
Если
– вектор, то
,
.
Задача 5.
Показать, что компоненты
,
где
– вектор, не зависят от коэффициентов
связности.
Решение.
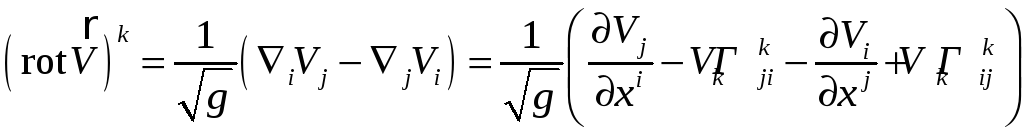
при
(справедливо в римановом пространстве);
требуемое доказано.
П.4. Оператор материального дифференцирования по времени имеет вид:
,
примененный к
вектору
,
имеет вид:
.
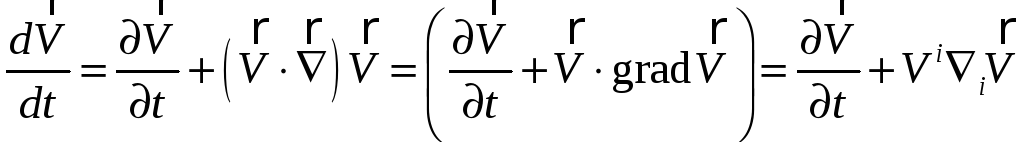Контравариантные
компоненты вектора
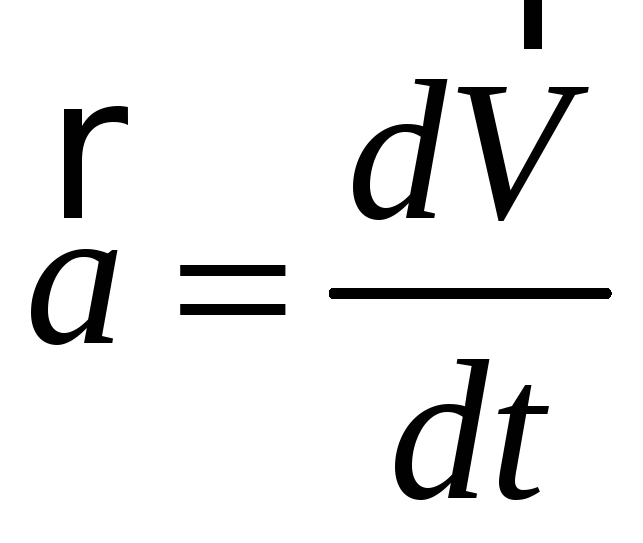равны
.
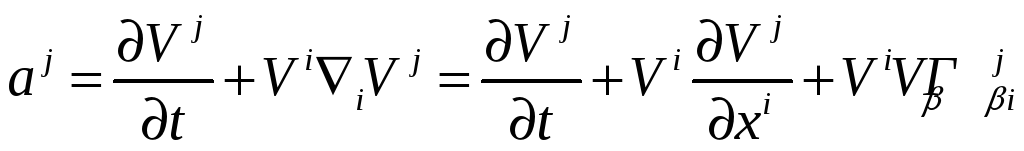Задача
6. Записать
компоненты вектора
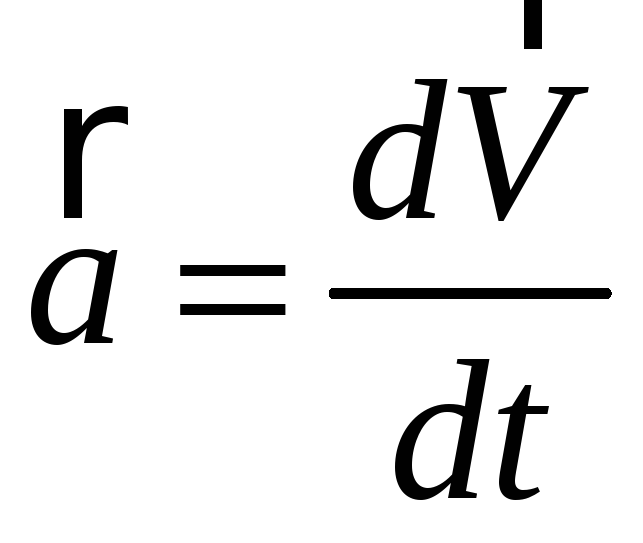в сферической системе координат.
Решение. Используя решение задачи 6 (занятие 7), получим:
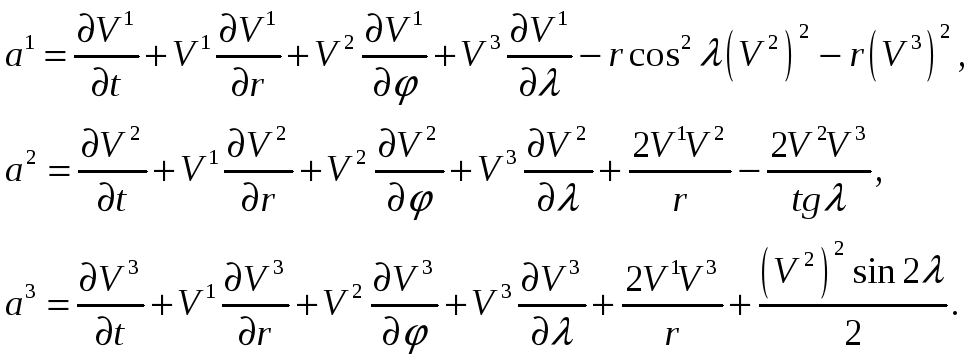
Дополнительные задачи.
-
Записать выражение лапласиана в цилиндрической системе координат.
Решение.
В ортогональных координатах
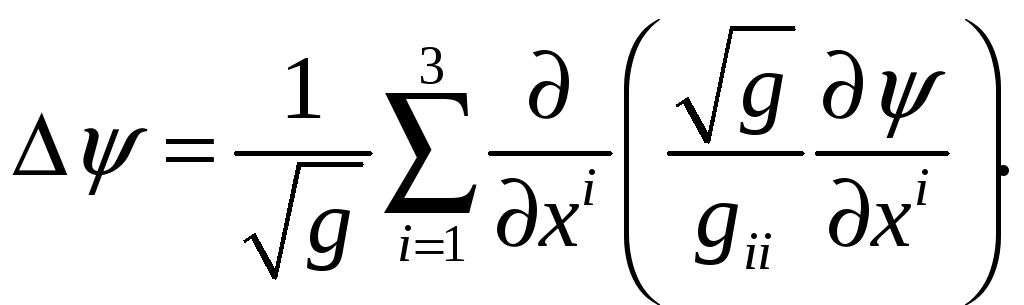
В случае цилиндрической системы координат
Лапласиан запишется в виде
-
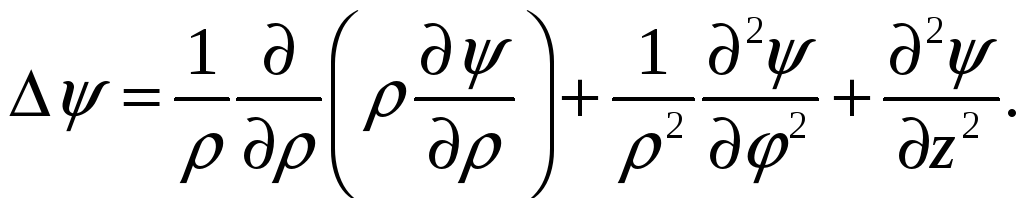
Показать справедливость представления ковариантных компонент векторного произведения
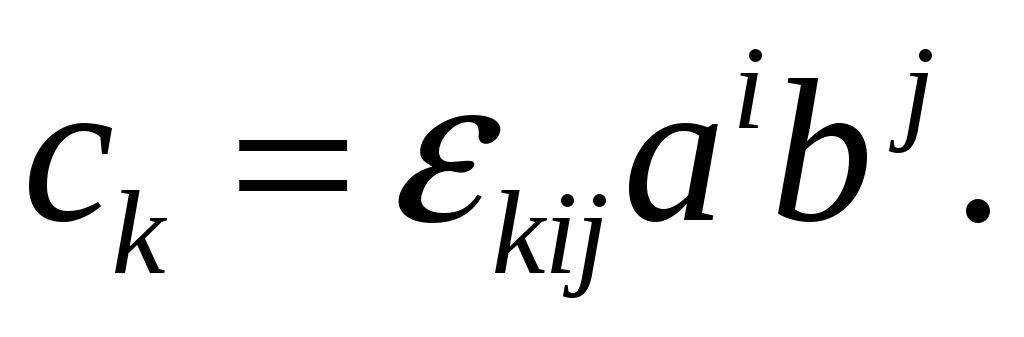
Решение.
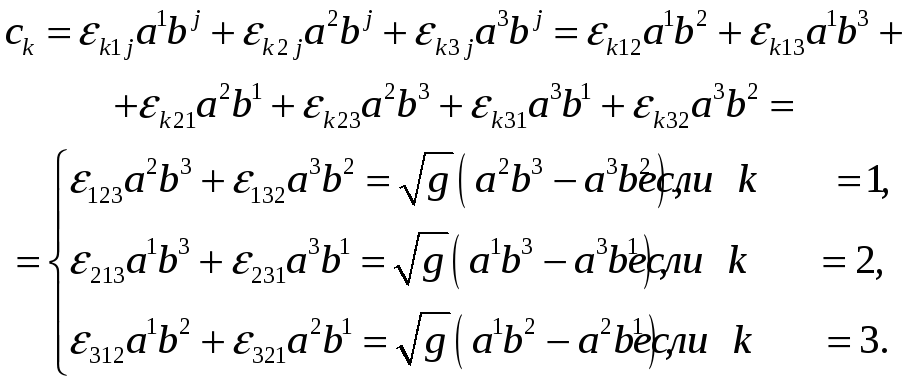
Что требовалось показать.
-
Записать компоненты
,
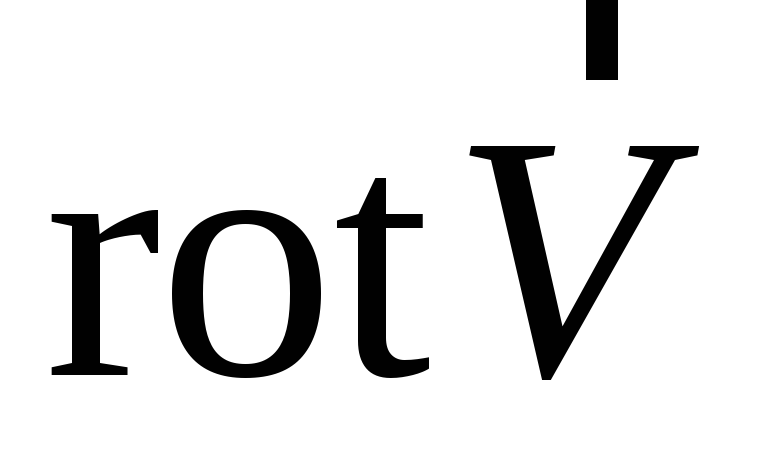– вектор в декартовых координатах.
Решение.
В ортогональных координатах
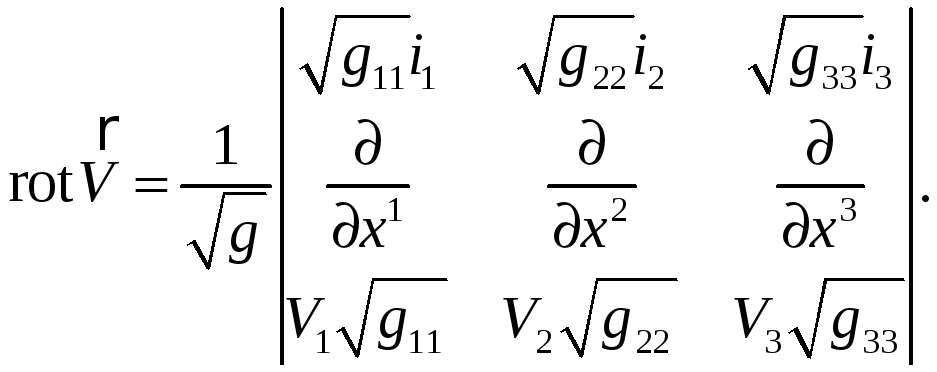
В случае декартовой системы координат
Ответ.
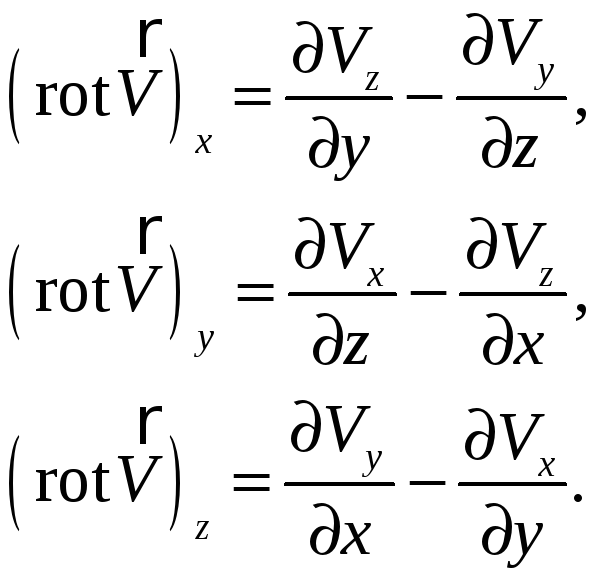
План занятия
|
Время |
Длительность, мин. |
Название мероприятия |
|
00:00 – 00:05 |
5 |
Учет в журнале отсутствующих, быстрая проверка наличия письменного решения домашнего задания. |
|
00:05 – 00:15 |
10 |
Разбор на доске не решенных упражнений из домашнего задания. |
|
00:15 – 00:25 |
10 |
Введение в новую тему. П.1. Определение лапласиана. Разбор задачи №1 и №2. |
|
00:25 – 00:45 |
20 |
П.2. Определение векторного произведения. Задачи № 3 и №4 ввиду их легкости рекомендуется решить студентам у доски. |
|
00:45 – 00:55 |
10 |
П.3. Определение оператора «ротор». Решение задачи №5. |
|
00:55 – 01:15 |
20 |
П.4. Определение материальной производной по времени. Задача №6 рекомендуется для самостоятельного решения студентами на занятии. |
|
01:15 – 01:20 |
5 |
Задание домашней работы: решить дополнительные задачи занятия. |
З а н я т и е 9
Тема. ЛАГРАНЖЕВО И ЭЙЛЕРОВО ОПИСАНИЕ СПЛОШНОЙ СРЕДЫ. ПОНЯТИЕ МАТЕРИАЛЬНОЙ ПРОИЗВОДНОЙ ПО ВРЕМЕНИ
п.1.
Лагранжева (материальная) система
координат
свя-
зана
с деформирующейся средой, эйлерова
(лабораторная) система координат
связана с наблюдателен за сплошной
средой. Если
какое-либо
свойство среды описано с помощью
переменных Лагран-ха (Эйлера),
)
, то имеем со-
ответственно лагранжево (эйлерово) описание.
Задача 1. Какое да двух соотношений дает эйлерово описание преобразования:
1)
2)
Ответ. Первое - эйлерово, второе - дагранжево. Задача 2. Дано описание движения сплошной среды ( конти-нуума)
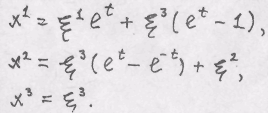
а) с какой точки зрения описано движение, Ответ. Лагранжево описание.
в) убедиться, что лагранжевы координаты точек сплошной среды совпадают со значениями эйлеровых координат в началаный момент времени.
Ответ.
При
с) Выразить лагранжевы координаты через эйлеровы. Ответ.
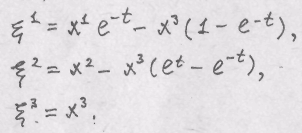
Задача 3. Описание движения сплошной среды, занимавшей первоначально куб со стороной, равной единице, дается выражениями задачи 2.
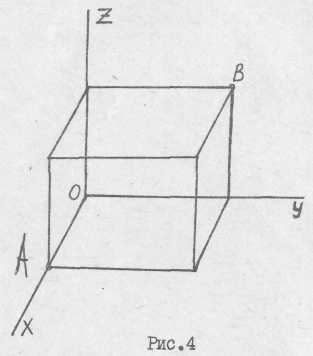
а) какое движение совершает точка А (рис.4).
Решение.
При
координаты точки равны
С течением времени
лагран-жевы координаты точки не меняются,
эти координаты - своеобраз -ная "метка"
точки (изменяется вид лагранжевых систем
координат, связанных с деформирующейся
средой). Эйлеровы координаты точки А
будут при этом равны;
Эйлеровы
(лабораторные) координатные линии с
течением времени не изменяются (оставаясь
декартовыми). Точка А будет двигаться
по оси
по закону
в)
Изучить движение точки
(рис.4).
Решение.
При
для точки
,
Движение точки
в
системе
описывается уравнениями:
Точка В будет двигаться в плоскости верхней грани куба по траектории с уравнением:
Так
как
, то точки, лежавшие первоначально в
плоскос-
ти,
параллельной
, остаются в ней с течением времени.
Такое движение сплошной среда называется деформацией чистого сдвига.
п.2. Материальная (полная, индивидуальная, субстанционная) производная величины ( ) выражает "скорость" изменения
С ) в данной точке, характеризующейся постоянными лаграшсе-выми координатами.
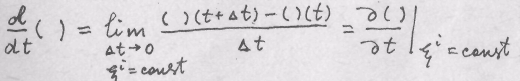
Задача 4. Определить компоненты вектора скорости точки сплошной среды как функции а) лагранжевых, б) эйлеровых координат и времени. Движение сплошной среды ведано соотношениями эадачи 2.
Решение. а)
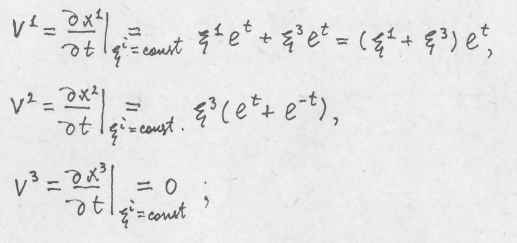
б)
учитывая эйлерово описание движения,
выразим
че-
рез
и
.В итоге имеем:
Дополнительные задачи.
1. Дано поле скоростей
Найти
компоненты ускорения
в эйлеровых и лагранже-
вых переменных. Ответ.
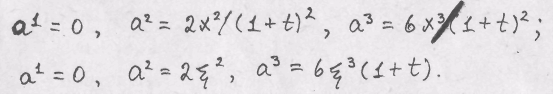
2. Движение континуума задано уравнениями:
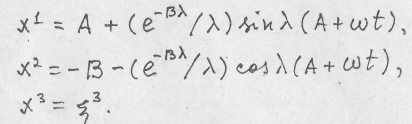
Доказать,
что траектории всех частиц - окружности,
а величина скорости постоянна. Определить
связь между
и
и лагран-
жевыми
координатами
и
,
совпадающими с
ЛИТЕРАТУРА