КАЗАНСКИЙ ОРДЕНА ЛЕНИНА И ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени В. И. УЛЬЯНОВА-ЛЕНИНА

МЕХАНИКА СПЛОШНОЙ СРЕДЫ

Методическая разработка практических занятий

КАЗАНЬ – 1987-2008

Утверждено на заседании кафедры аэрогидромеханики механико-математического факультета КГУ

Методическая разработка, предназначенная студентам и преподавателям при изучении курса механики сплошной среды по университетским программам, использовалась в течение ряда лег при проведении практических занятий со студентами-механиками II-III курсов.

Работа содержит элементы тензорного исчисления и кинематики.

Издание 2-е, переработанное, дополненное.

Составители

Профессор Клоков В. В.

Доцент Филатов Е. И.

Ассистент Насибулин В. Г.

Занятие 1

Тема. ЭЛЕМЕНТЫ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ. БАЗИСНЫЕ ВЕКТОРЫ. СОГЛАШЕНИЕ О СУММИРОВАНИИ. МЕТРИЧЕСКАЯ МАТРИЦА.

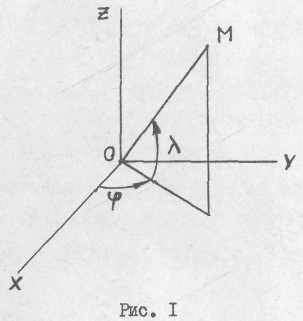
п.1. Криволинейные координаты изучаются на примере сферической системы координат (рис,1). Используем обозначения .

Координатной поверхностью называют геометрическое место точек, для которых указанная координата постоянна. Например, в координатной плоскости декартовой прямолинейной системы координата ее точек постоянна и равна нулю.

Координатной линией называют геометрическое место точек, для которых одна и только одна координата переменна. Координатные линии – пересечения координатных поверхностей.

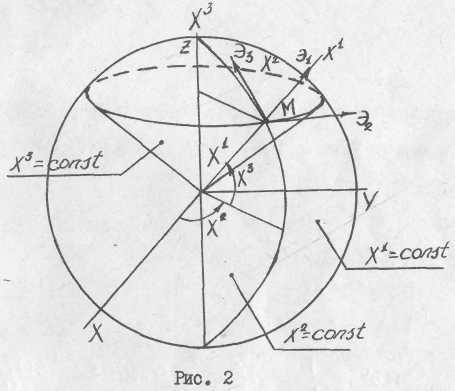
Задача 1. Определить координатные поверхности введенной сферической системы координат, проходящие через точку М.

Ответ. Координатная поверхность – сфера радиуса с центром в точке ; координатная поверхность – полуплоскость, проходящая через ось и точку М; координатная поверхность _– коническая поверхность, ось симметрии которой – , образующая, составляет с осью угол .Поверхности указаны на рис.2.

Задача 2. Определить координатные линии введенной сферической системы координат, проходящие через точку М.

Ответ. Координатная линия – луч, проходящий через и ; координатная линия – окружность радиуса _, плоскость которой параллельна ; координатная линия _– полуокружность радиуса , лежащая в координатной плоскости _.

п.2. Базисные векторы (или векторы базиса) по определению равны

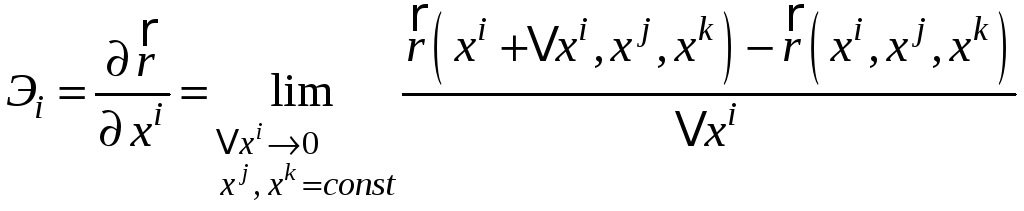
направлены по касательным к координатным линиям в точке М в сторону возрастания соответствующей кооординаты (индексы могут принимать значения 1, 2, 3 и расположены в циклическом порядке). Концы векторов, стоящих в числителе дроби, лежат на координатной линии _.

Задача 3. Показать, что касательные к координатным линиям в точке М введенной сферической системы координат взаимно перпендикулярны.

Ответ. Касательные лежат во взаимно перпендикулярных плоскостях, следовательно, они взаимно перпендикулярны. (Полезно доказать также с использованием теоремы о трех перпендикулярах).

Задача 4. Определить модули векторов базиса введенной сферической системы координат в точке М.

Решение. Величина

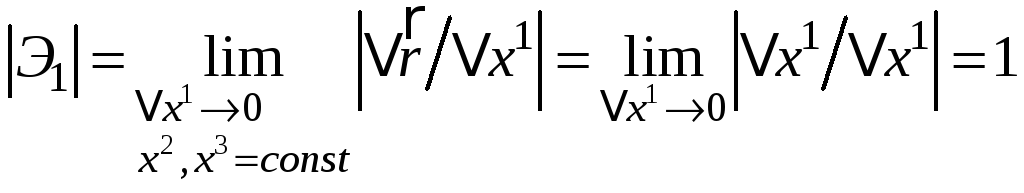, здесь , где _M и _N - точки, лежащие на координатной линии (рис.3). Величины

,

.

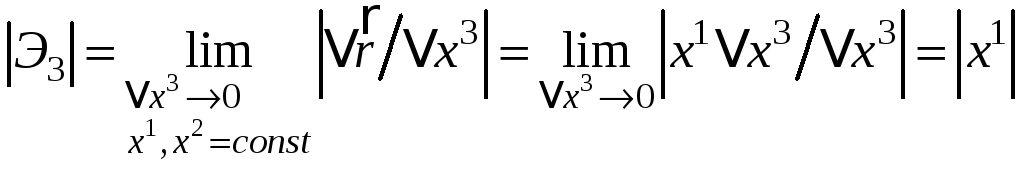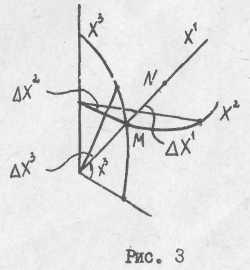
В зависимости от положения точки М изменяются, вообще говоря, направления и величины базисных векторов.

п.3. Соглашение о суммировании (введено А.Эйнштейном) по немым индексам (один из них, ковариантный, расположен снизу индексируемой величины, а другой, контравариантный, сверху) означает, что 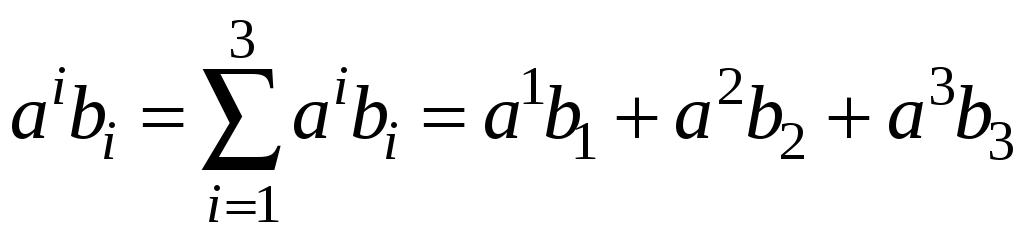Немые индексы можно обозначать различными буквами.

Упражнения. Дать развернутую запись

1. Ответ: , индекс _– свободный (по нему нет суммирования).

Если – символ Кронекера, то .

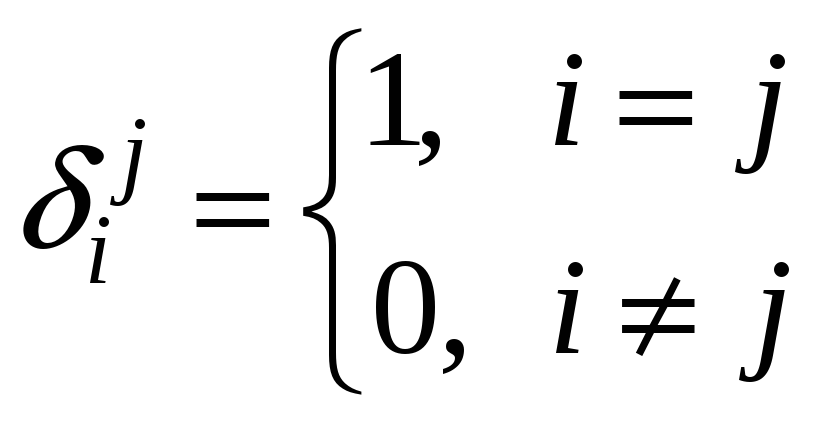2. _{Ответ: .}

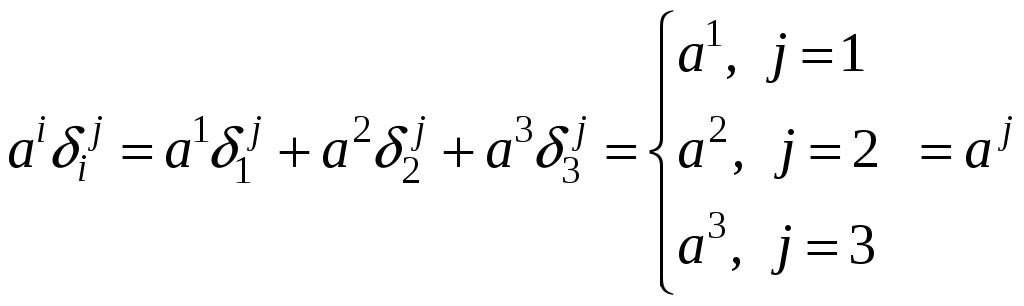3. Ответ: .

4. Ответ: .

Разложим вектор , соединяющий пару бесконечно близких точек M и _N, по направлениям базисных векторов в точке M. .

п.4. Метрическая матрица позволяет выразить квадрат расстояния между M и N в виде:

.

Матрица из коэффициентов 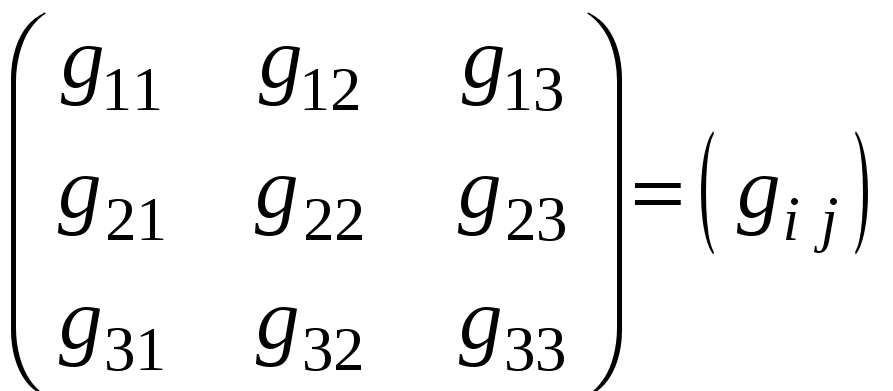называется метрической. Первый индекс означает номер строки, второй – столбца.

Упражнение. Дать развернутую запись .

Ответ:

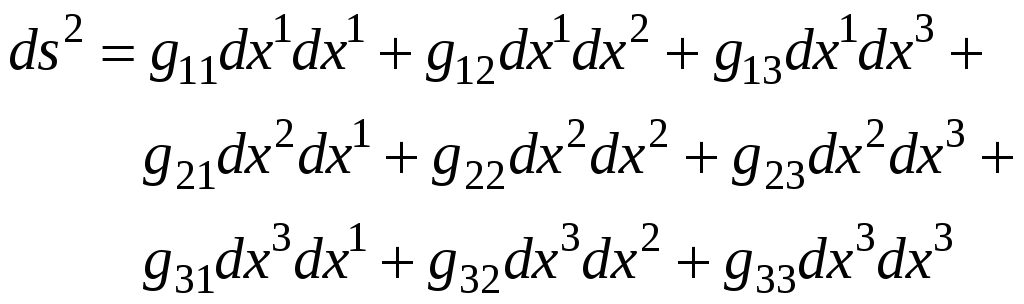
Задача 5. Найти компоненты в точке M в случае введенной сферической системы.

Решение. Запишем выражение длины внутренней диагонали прямоугольного параллелепипеда, сторонами которого являются , , .

Тогда . Сравнивая полученное соотношение с раскрытым выше выражением, получаем матрицу:

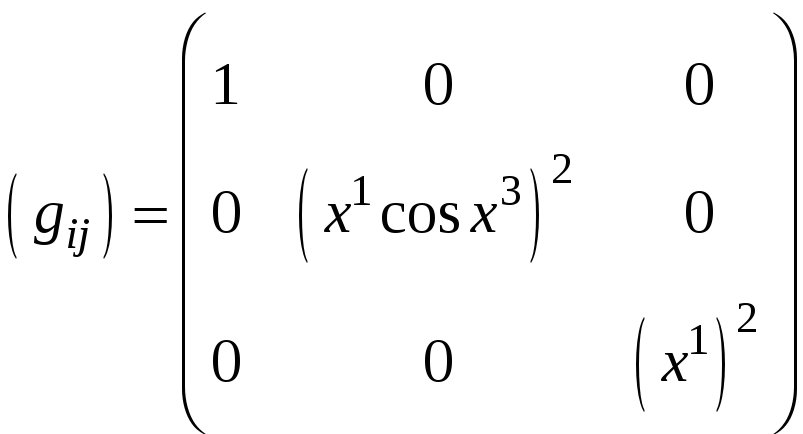
Это симметричная матрица с нулевыми недиагональными элементами, что характерно для рассматриваемой ортогональной системы координат.

п.5. Сопряженной матрицей или обратной к матрице метрической называется матрица , если элементы этих двух матриц связаны следующим образом:

или ,

где – элементы транспонированной матрицы ; – алгебраическое дополнение к элементу , – определитель матрицы . , – миноры к элементу .

Задача 6. Найти матрицу, обратную к матрице метрической в точке M, введенной сферической системы координат.

Решение. Так как

,

,

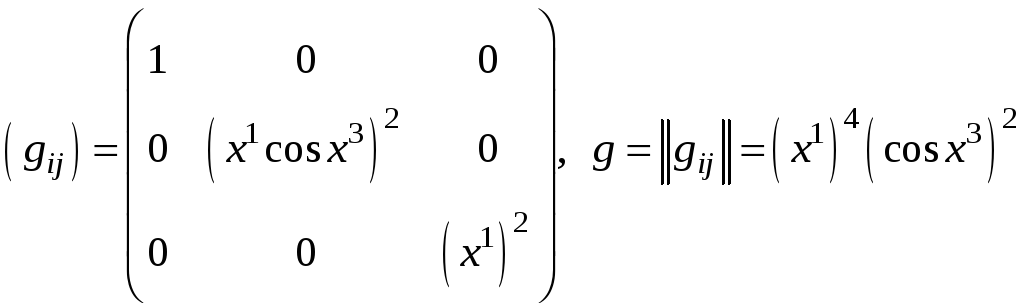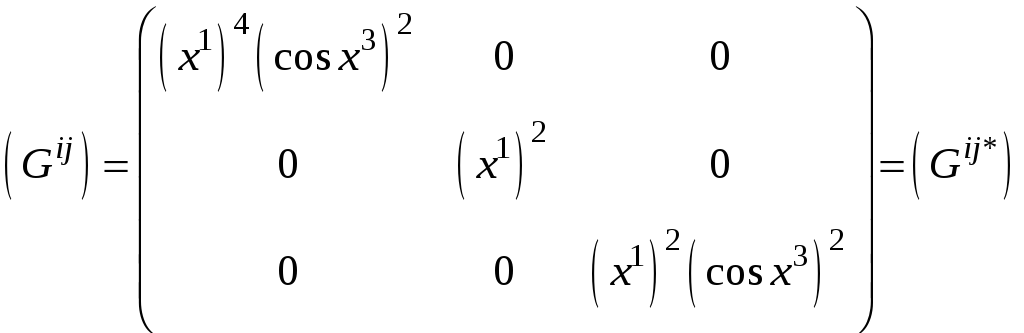то искомая обратная матрица имеет виц:

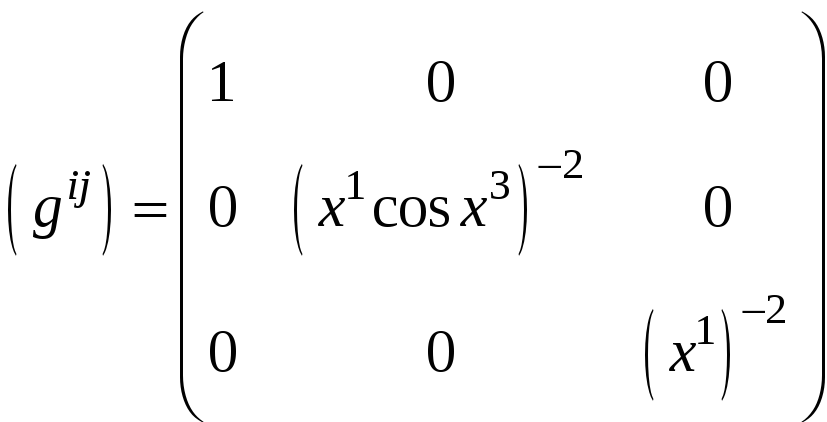.Элементы матриц определены при .

п.6. Сопряженный (обратный, контравариантный) базис векторов определяется выражением:

Задача 7. Найти разложение базисных векторов по базисным векторам в точке M в случае введенной сферической системы координат.

Решение: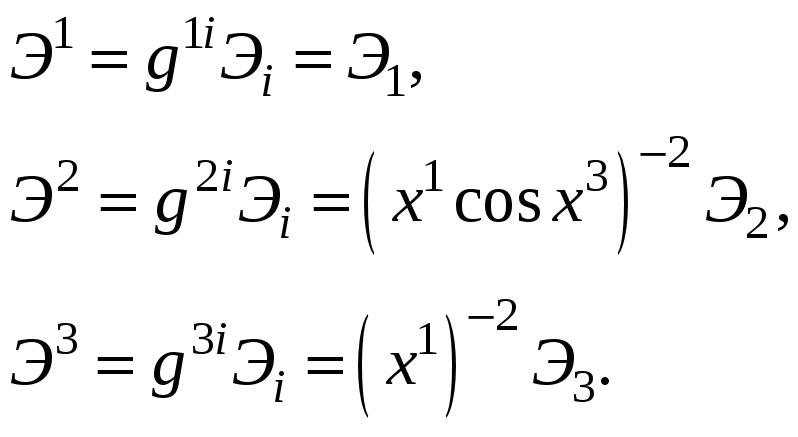

Дополнительные задачи.

1. Решить задачи 1-7 в случае цилиндрической системы координат.

2. Доказать, что .

3. Доказать, что .

4. Доказать, что .

5. Упростить выражения .

6. Упростить выражение , если .

7. Вычислить , .