Занятие 3

Тема. ИНВАРИАНТНЫЕ ОБЪЕКТЫ, ВЕКТ0Р.ДИАДА.ТЕН30Р.

п.1. Инвариантными относительно преобразования координат называют свойства, не меняющиеся при названном преобразовании. Примером служат скалярные величины.

В частности, инвариантным является квадрат расстояния между близкими точками

.

Задача 1. Убедиться в инвариантности предыдущего представ­ления.

Решение. используем формулы преобразования и при переходе от старых координат к новым. Имеем

.

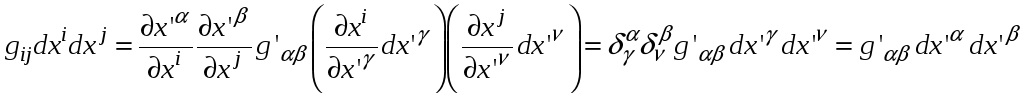П.2. Вектор - линейная комбинация базисных векторов, он характеризуется инвариантной формой представления. . Здесь - вектор базиса, - компоненты вектора в данном базисе.

Задача 2. Показать инвариантность представления вектора в различных системах координат.

Решение. Используем формулы преобразования и .

.

Из инвариантности представления вектора следует другое определение вектора, компоненты разложения которого в данном базисе при переходе к новому базису изменяются по формуле: .

Задача 3. Доказать последнее утверждение.

Решение. Имеем равенство: . Учтем связь базисных векторов при переходе к новой системе координат. Тогда ; из сравнения сомножителей имеем , и т.д. Результат сложения векторов есть вектор, компоненты которого есть сумма компонентов слагаемых в том же базисе.

Задача 4. Показать, что если , то в общем случае не может быть компонентой вектора.

Решение. Если бы это было так, то , что, вообще говоря, неверно. Расположение индексов несущественно, если компонента берется в декартовой системе координат.

Задача 5. Привести различные формы представления вектора .

Решение. . Как следствие доказать .

Задача 6. Доказать инвариантность представления скалярного произведения векторов.

Решение.

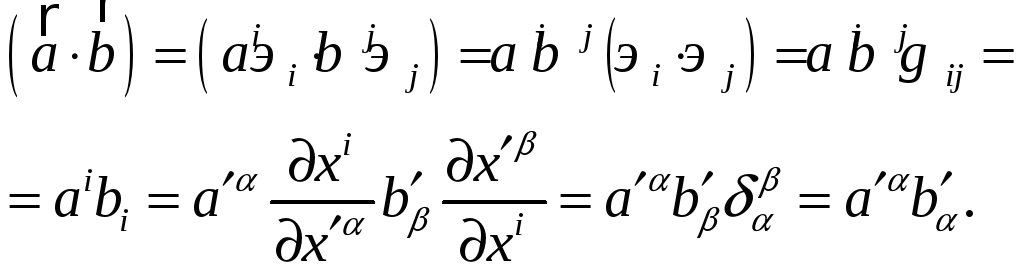
П.3. Диада - элемент девятимерного линейного пространства, характеризуется разложением: . Здесь , образуют базис пространства.

Задача 7. Записать всевозможные диады из ортов декартовой системы координат .

Решение. - эти диады составляют линейно независимую систему диад, соответствующих декартовой системе координат, и образуют базис, с помощью которого может быть представлена любая диада. Последняя характеризуется матрицей из коэффициентов линейной комбинации элементов базиса. Например, - девятичленная форма диады, соответствующая ей матрица . Матрица, соответствующая девятичленной форме диады , имеет вид:

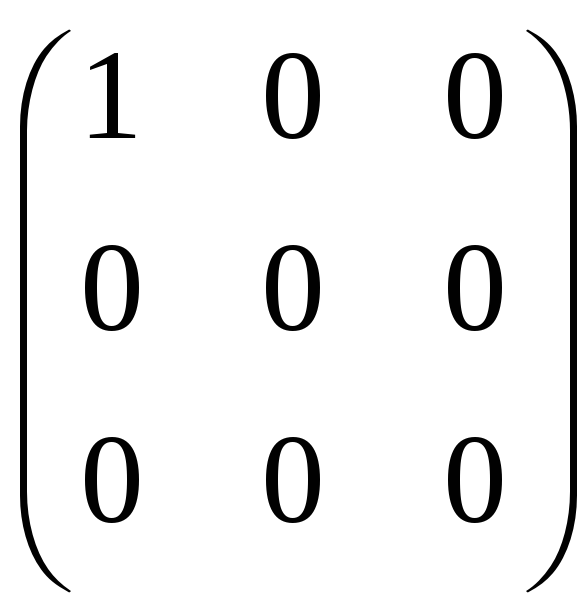
П.4. Тензор 2-го ранга (2-ой валентности) – линейная комбинация диад базисных векторов, инвариантная относительно непрерывного, взаимнооднозначного преобразования координат (точнее – относительно группы преобразований). Одна из форм представления тензора 2-го ранга , число индексов у компонент тензора определяет его ранг. Скаляр - тензор нулевого ранга, вектор – первого.

Задача 8. Представить все формы записи тензоров 2-го ранга.

Решение. .

П.5. Метрический тензор. в качестве компонент имеет элементы метрической матрицы.

.

Задача 9. Найти формулу преобразования ковариантных компонентов тензора 2-го ранга при переходе к новой системе координат.

Решение. Из инвариантной формы представления тензора и формулы преобразования векторов взаимного базиса имеем равенство: . Из сравнения левой и правой частей следует искомая формула: . Если индексированные величины при переходе к новой системе координат преобразуются по выше записанной формуле, то эти величины можно рассматривать в качестве компонент тензора . Сам тензор представляется заданием как , так и диад .

Задача 10. Найти формулу преобразования компонент со смешанным строением индексов при переходе к новой системе координат.

Решение.

. Из сравнения получаем .

Дополнительные задачи.

1. Показать, что при умножении вектора 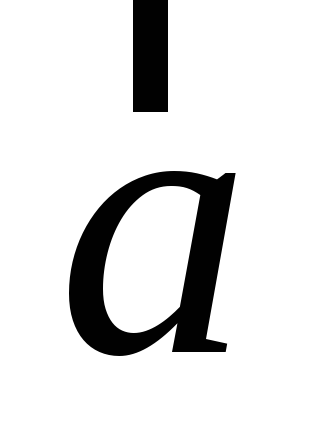на скаляр получается векторная величина 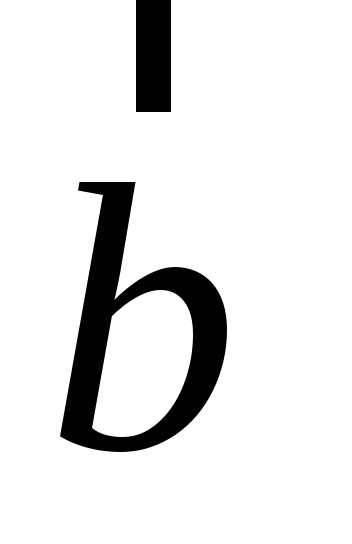с компонентами .

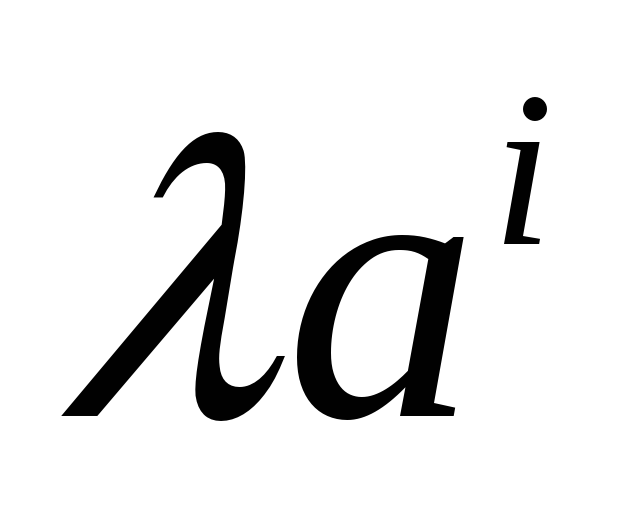Решение. .

2. Записать матрицу диады, составленной из векторо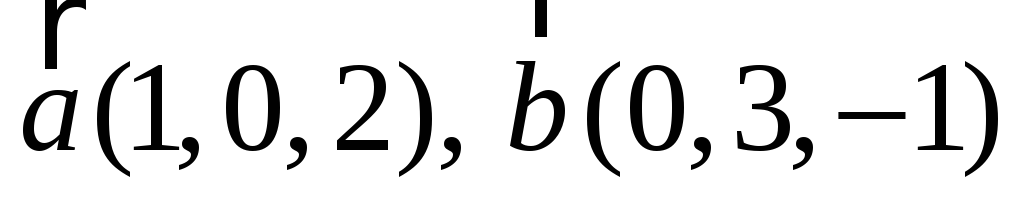в , где в скобках указаны декартовы компоненты векторов.

Ответ.

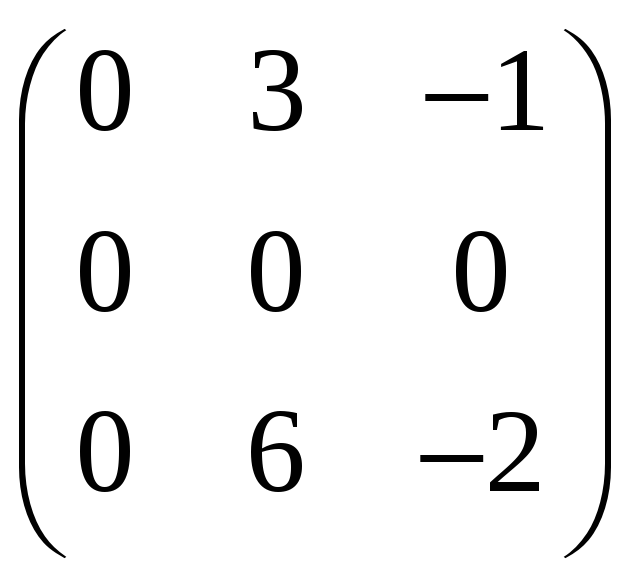
Решение. . Используя решение задачи 7 имеем

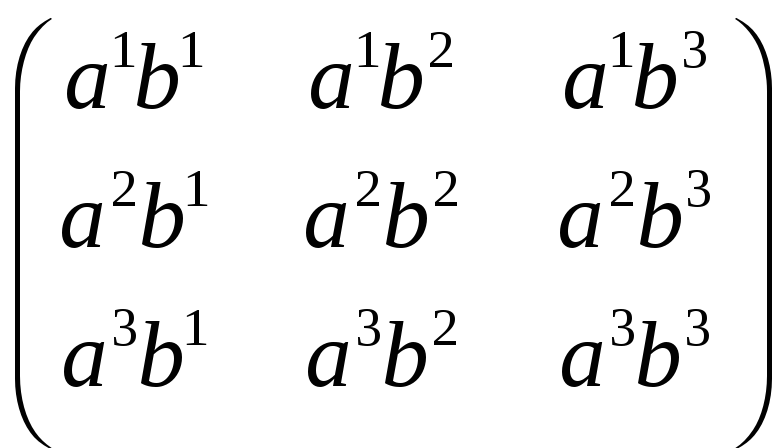
3. Записать метрический тензор в сферической системе координат.

Решение. .

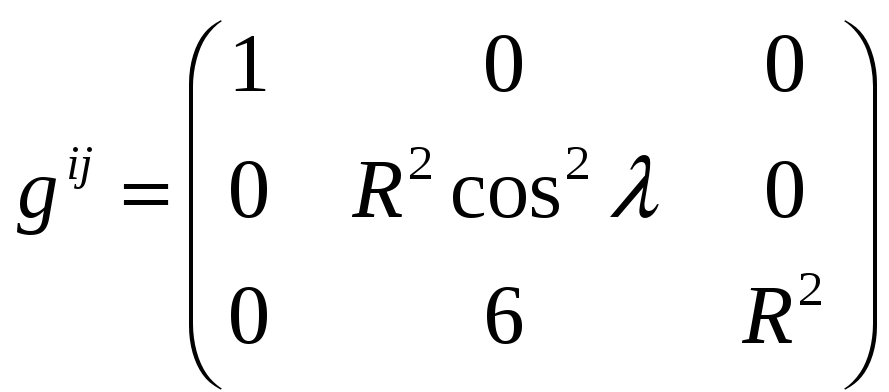
4. Получить формулы преобразования компонент 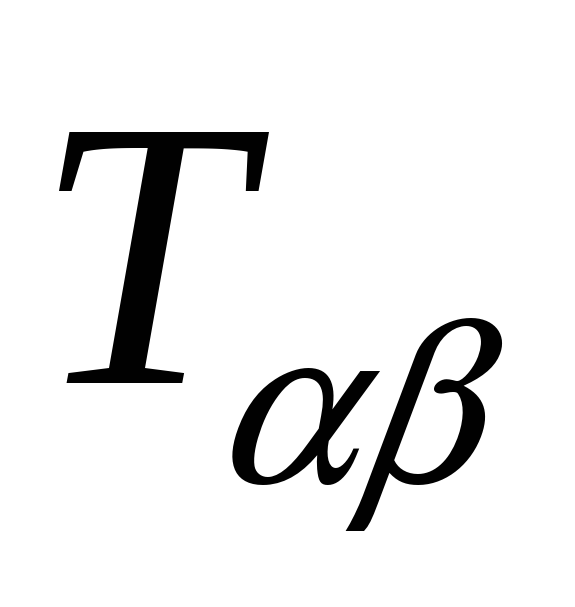тензора при переходе от сферической системы к декартовой.

Решение. .

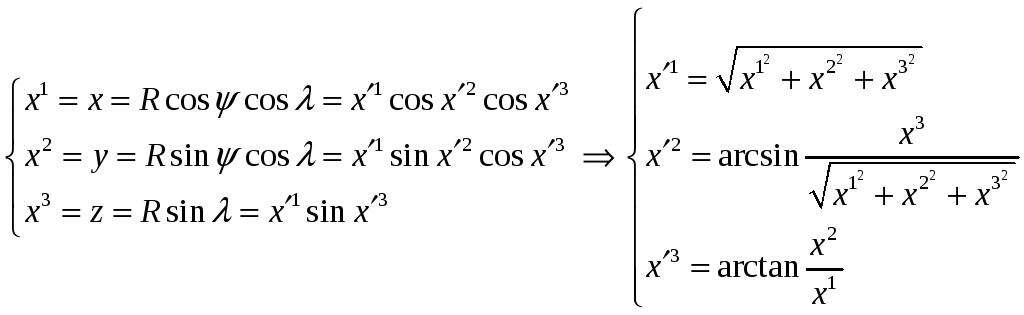
Далее используем соотношение из Задачи 9.

План занятия (80 мин).

1. Проверка домашнего задания (10 мин). Возможно, показать ход решения задачи, которую ни у кого не получилось решить (+5 мин).

2. Введение в новую тему. Теоретическая часть: инвариантность, вектор. + Решение у доски преподавателем задачи по теме занятия (Задача 1) (10 мин).

3. Самостоятельное решение задач студентами с вызовом к доске (Задачи 2,3,5, Доп. задача 1) (20 мин).

4. Введение в новую тему. Теоретическая часть: диада, тензор 2-го ранга. + Решение у доски преподавателем задачи по теме занятия (Задача 7) (10 мин).

5. Самостоятельное решение задач студентами с вызовом к доске (Доп. задача 2, Задачи 8,9) (20 мин).

6. Задание на дом (Задачи 4,6,10, Доп. задачи 3,4) (5 мин).