
- •Предел и непрерывность функции одной переменной
- •Введение. Множества и операции над ними
- •Примеры числовых множеств, их стандартные обозначения
- •Пустое множество
- •Включение множеств
- •Равенство множеств
- •Операции над множествами
- •Эквивалентность множеств
- •Мощность множества
- •§ 1. Функция
- •Способы задания функции
- •Аналитический способ задания функции.
- •Табличный способ задания функции.
- •Графический способ задания функции.
- •График функции
- •Обратная функция
- •Основные элементарные функции
- •4) Тригонометрические функции.
- •5) Обратные тригонометрические функции.
- •Суперпозиция функций
- •Классификация функций
- •Задачи к § 1
- •§ 2. Бесконечно малые функции
- •Задачи к §2
- •§ 3. Свойства бесконечно малых функций
- •Задачи к §3
- •§ 4. Бесконечно большие функции
- •Задачи к §4
- •§ 5. Предел функции
- •Односторонние пределы
- •Свойства предела функции
- •Задачи к §5
- •§ 6. Теоремы о вычислении предела функции. Неопределенности
- •Задачи к §6
- •§ 7. Замечательные пределы
- •2) Число . Натуральные логарифмы
- •§ 8. Сравнение бесконечно малых. Эквивалентные бесконечно малые
- •Вычисление пределов степенно-показательных функций
- •Задачи к §8
- •§ 9. Непрерывность функции
- •Второе определение непрерывности
- •Точки разрыва
- •Свойства функций, непрерывных на замкнутом промежутке
- •Задачи к §9
- •Литература
- •Оглавление
Способы задания функции
-
Аналитический способ задания функции.
А) Явный способ
задания функции.
Если правило
![]() ,
по которому устанавливается соответствие
между элементами множеств
,
по которому устанавливается соответствие
между элементами множеств
![]() и
и
![]() ,
задается в виде формулы, указывающей,
какие действия необходимо произвести
над переменной
,
задается в виде формулы, указывающей,
какие действия необходимо произвести
над переменной
![]() ,
чтобы получить значение
,
чтобы получить значение
![]() ,
то такой способ задания называется
явным.
В этом случае
область определения
,
то такой способ задания называется
явным.
В этом случае
область определения
![]() и область изменения
и область изменения
![]() определяются, как правило, самой формулой.
определяются, как правило, самой формулой.
Пример 1.1. Функция
![]() задается формулой
задается формулой
![]() .
.
Область задания
![]() определяется системой:
определяется системой:
![]()
Решаем данную систему:
![]()
![]()
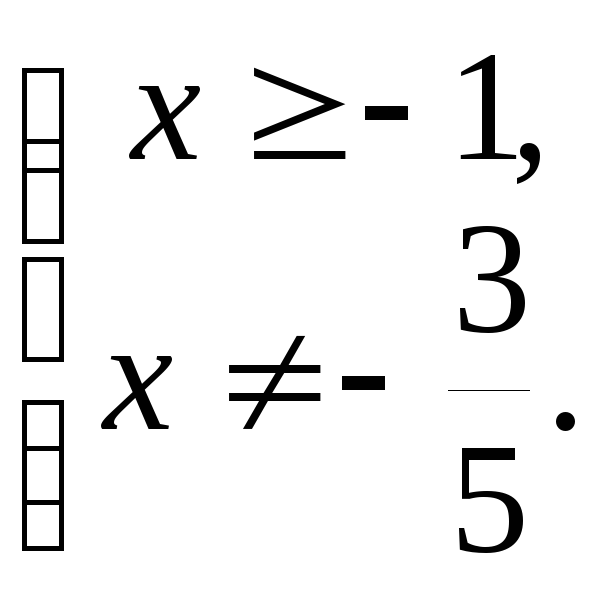
![]()
![]() .
.
Следовательно,
![]() .
.
Следует отметить,
что при явном задании функции для разных
подмножеств множества
![]() могут быть использованы разные формулы.
могут быть использованы разные формулы.
Пример 1.2.
![]()
Б) Неявный способ
задания функции.
Если
соответствие между элементами множеств
![]() и
и
![]() задается в виде уравнения
задается в виде уравнения
![]() ,
,
связывающего
переменные
![]() и
и
![]() ,
то такой способ задания называется
неявным.
При этом, если для любого
,
то такой способ задания называется
неявным.
При этом, если для любого
![]() из некоторого множества
из некоторого множества
![]() существует значение
существует значение
![]() ,
которое совместно с
,
которое совместно с
![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() ,
то тем самым определена функция
,
то тем самым определена функция
![]() .
.
Пример 1.3. Уравнение
![]()
определяет
![]() как функцию
как функцию
![]() ,
при этом
,
при этом
![]() можно явно выразить через
можно явно выразить через
![]() .
.
Пример 1.4. Уравнение
![]()
определяет
![]() как функцию
как функцию
![]() ,
при этом
,
при этом
![]() невозможно явно выразить через
невозможно явно выразить через
![]() .
.
Заметим, что
![]() является тождеством.
является тождеством.
В)
Параметрический способ задания функции.
Пусть на
множестве
![]() заданы две функции:
заданы две функции:
![]() и
и
![]() ,
имеющие области значений
,
имеющие области значений
![]() и
и
![]() соответственно. Пусть правило
соответственно. Пусть правило
![]() ,
по которому устанавливается соответствие
между элементами множеств
,
по которому устанавливается соответствие
между элементами множеств
![]() и
и
![]() ,
задается с помощью системы
,
задается с помощью системы
![]() (
(![]() )
)
Такой способ
задания функции называется параметрическим,
а переменная
![]() –
параметром.
–
параметром.
Пример 1.5.
Функция
![]() задается уравнениями
задается уравнениями
 (
(![]() )
)
где
![]() – положительное число.
– положительное число.
-
Словесный способ задания функции.
Если правило
![]() ,
по которому устанавливается соответствие
между множествами
,
по которому устанавливается соответствие
между множествами
![]() и
и
![]() описывается словами, то такой способ
задания называется словесным.
описывается словами, то такой способ
задания называется словесным.
Пример 1.6.
Функция
![]() определяется как наибольшее целое
число, не превосходящее
определяется как наибольшее целое
число, не превосходящее
![]() .
Тем самым
.
Тем самым
![]() определена для любого
определена для любого
![]() .
Так,
.
Так,
![]() ,
,
![]() ,
,
![]() .
.
-
Табличный способ задания функции.
Если правило
![]() ,
по которому устанавливается соответствие
между множествами
,
по которому устанавливается соответствие
между множествами
![]() и
и
![]() ,
задается в виде таблицы, в которой
указываются пары соответствующих
элементов этих множеств, то такой способ
задания называется табличным.
,
задается в виде таблицы, в которой
указываются пары соответствующих
элементов этих множеств, то такой способ
задания называется табличным.
Как правило, такой способ задания возникает при экспериментальном изучении функциональных зависимостей, когда в таблице сопоставляются полученные из опыта данные.
-
Графический способ задания функции.
Если правило
![]() ,
по которому устанавливается соответствие
между множествами
,
по которому устанавливается соответствие
между множествами
![]() и
и
![]() ,
задается в виде кривой на плоскости
,
задается в виде кривой на плоскости
![]() ,
координатами точек которой являются
пары
,
координатами точек которой являются
пары
![]() значений
значений
![]() и соответствующего ему
и соответствующего ему
![]() ,
то такой способ задания называется
графическим.
,
то такой способ задания называется
графическим.
Табличный и графический способы задания функции в данном пособии рассматриваться не будут.
График функции
Пусть на множестве
![]() задана функция
задана функция
![]() .
Определим на плоскости прямоугольную
декартову систему координат
.
Определим на плоскости прямоугольную
декартову систему координат
![]() .
Каждой паре
.
Каждой паре
![]() значений аргумента и функции соответствует
точка
значений аргумента и функции соответствует
точка
![]() на плоскости
на плоскости
![]() .
Когда переменная
.
Когда переменная
![]() меняется в пределах своей области
задания
меняется в пределах своей области
задания
![]() ,
эта точка описывает некоторую кривую,
которая называется графиком
функции.
,
эта точка описывает некоторую кривую,
которая называется графиком
функции.
График однозначной функции обладает следующим свойством: любая вертикальная прямая может пересекать график не более чем в одной точке.
В качестве примера
приведем график функции
![]() (рис. 1.1), описанной в примере 1.6.
2
(рис. 1.1), описанной в примере 1.6.
2

Рис. 1.1.
