§ 8. Сравнение бесконечно малых. Эквивалентные бесконечно малые
Заметим, что
функции, бесконечно малые в одной и той
же точке, могут стремиться к нулю
по-разному. Так,
стремится к
при
гораздо «быстрее», чем
и гораздо «медленнее», чем
(рис. 8.1). Чтобы провести сравнение двух
бесконечно малых в окрестности одной
и той же точки функций, рассматривают
предел их отношения.
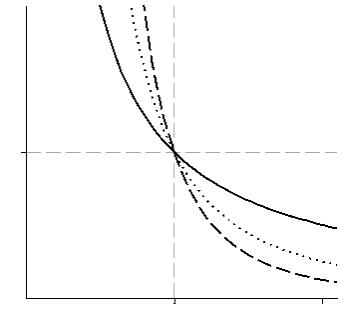
Рис. 8.1.
Определение 8.1.
1) Говорят, что
бесконечно малая в точке
(в бесконечно удаленной точке) функция
имеет в этой точке более высокий порядок
малости, чем бесконечно малая
,
если
.
При этом
говорят, что
имеет в
данной точке более низкий порядок
малости, чем
.
2) Говорят, что
бесконечно
малые в точке
(в бесконечно удаленной точке) функции
и
имеют в этой точке одинаковый порядок
малости,
если
.
Среди пар бесконечно
малых одинакового порядка особое место
занимают те пары, для которых
.
Определение 8.2.
Говорят, что
бесконечно
малые в точке
(в бесконечно удаленной точке) функции
и
являются эквивалентными в этой точке,
если
.
Если бесконечно
малая
имеет более высокий порядок малости,
чем бесконечно малая
,
то этот факт обозначается следующим
образом
и читается так: «
есть о-малое от
».
Если бесконечно
малые
и
имеют одинаковый порядок малости, то
этот факт обозначается следующим
образом:
и читается так: «
есть О-большое от
».
Эквивалентность бесконечно малых обозначается следующим образом:
.
Результаты §7
позволяют назвать следующие пары
эквивалентных бесконечно малых в точке
функций:
,
(8.1)
,
(8.2)
,
(8.3)
.
(8.4)
Помимо приведенных
выше, существует
еще ряд пар бесконечно малых
в точке
функций, эквивалентность которых
нуждается в обосновании.
Теорема 8.1.
В точке
,
(8.5)
,
(8.6)
,
(8.7)
.
(8.8)
Доказательство. Докажем соотношения (8.5)–(8.8), непосредственно используя определение 8.2. Последовательно применяя теоремы 6.1, 7.1 и 6.2 имеем
.
что означает
эквивалентность функций
и
.
Для доказательства
утверждения (8.6) введем переменную
,
откуда
.
В силу теоремы 6.1
при
.
Тогда
,
что означает
эквивалентность функций
и
.
Для доказательства
утверждения (8.7) введем переменную
.
Тогда
.
В силу теоремы 6.1
.
Опираясь на доказанное выше соотношение
(8.5), получим:
,
что означает
эквивалентность функций
и
.
Для доказательства
(8.8) используем формулу
.
Тогда
,
что означает
эквивалентность функций
и
.
Замечание 8.1.
Эквивалентные бесконечно малые обладают
следующим свойством:
если для бесконечно малых в точке
(в бесконечно удаленной точке) функций
выполнены условия
,
,
то в этой точке
.
Этот факт проверяется рассуждениями
.
Например, в точке
.
Можно продолжить цепочку:
.
Эквивалентность бесконечно малых играет особую роль при раскрытии неопределенностей.
Теорема 8.2.
Пусть
,
являются бесконечно малыми в точке
(в бесконечно удаленной точке). Пусть в
этой точке этим функциям соответственно
эквивалентны бесконечно малые
,
.
Тогда
.
Доказательство.
.
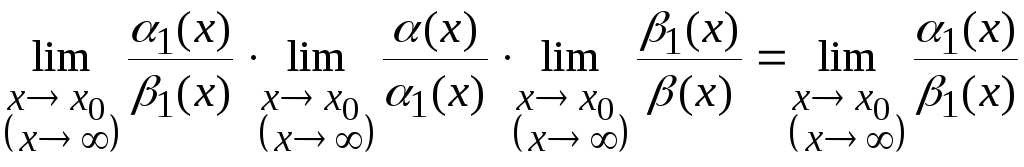Теорема доказана.
Замечание 8.2.
Из теоремы 8.2 следует, что при раскрытии
неопределенности типа
бесконечно малые функции, входящие в
числитель и/или знаменатель как множители,
можно заменять эквивалентными им
бесконечно малыми.
Заметим, что далеко не всегда бесконечно малые функции в числителе или знаменателе имеют вид, позволяющий непосредственно применять формулы (8.1)–(8.8). Как правило, числитель и/или знаменатель следует предварительно преобразовать. Очень часто приходится преобразовывать разность, стремящуюся к 0, в произведение. Это касается, в первую очередь, тригонометрических функций. Разность логарифмов одного и того же основания обычно преобразовывают к логарифму частного. Чтобы воспользоваться соотношениями (8.2) и (8.4), следует выделить число 1 как слагаемое либо под знаком логарифма, либо в основании степени. Преобразуя тригонометрические выражения, часто приходится использовать формулы приведения. Конечно, приходится прибегать и к преобразованиям другого типа.
Пример 8.1.
Вычислить
.
Решение. Используя
соотношения (8.8)
и (8.2) соответственно,
заменим
бесконечно малые
и
эквивалентными. Получим
.