Задачи к §4
Задача 1. Доказать, справедливость следующих утверждений:
а) функция
является бесконечно большой в точке
;
б) функция
является
бесконечно большой в бесконечно удаленной
точке;
в) функция
является бесконечно большой в точке
;
г) функция
является бесконечно малой в бесконечно
удаленной точке.
Указание. В рассматриваемых задачах воспользоваться теоремой 4.1 и результатами задач к §§ 1-3.
Решение.
а) Так как функция
является бесконечно малой в точке
(см. задачу 1 а) к §2), то
– бесконечно большая в этой же точке.
б) Функция
– бесконечно малая в бесконечно удаленной
точке (см. задачу 2 а) к §2). Следовательно,
– бесконечно большая там же.
в) Функцию
представляем в виде
,
где
– бесконечно малая в точке
функция (см. задачу 1 б) к §2). Следовательно,
– бесконечно большая в той же точке
функция.
г) Функцию
представляем в виде
,
где функция
–
бесконечно большая в бесконечно удаленной
точке (пример 4.2). Следовательно,
– бесконечно
малая в той же точке функция.
Задача 2.
Доказать, что частное
от деления бесконечно большой в точке
функции на функцию, локально ограниченную
в этой точке, является величиной
бесконечно большой.
Решение.
Пусть
– бесконечно большая, а
– локально ограниченная в точке
функции, заданные в некоторой
–окрестности
точки
.
В силу локальной ограниченности функции
существует такое число
(
),
что для всех
,
удовлетворяющих неравенству
,
выполнено неравенство
,
где
.
Зададимся произвольным числом
,
укажем число
и по нему найдем такое
(
),
что для всех
,
удовлетворяющих неравенствам
,
выполнено неравенство
.
Укажем
.
Очевидно
.
Указано такое
,
что для всех
,
удовлетворяющих неравенствам
,
будут справедливы оба неравенства,
откуда следует справедливость соотношения
.
В силу произвольности
теорема доказана.
Задача 3. Доказать, что:
а) функция
является бесконечно большой в точке
;
б) функция
является бесконечно большой в бесконечно
удаленной точке.
Указание. Воспользоваться утверждением, доказанным в задаче 2.
Решение.
а) Функцию
представим в виде
.
По теореме 4.1 функция
является бесконечно большой в точке
,
поскольку
– бесконечно малая в этой точке функция
(см. замечание 2.3). Так как для всех
,
удовлетворяющих неравенству
выполнены неравенства:
,
то функция
локально
ограничена в точке
.
По доказанному в
задаче 2 утверждению получим, что
является бесконечно большой в точке
функцией.
б) Функции
и
являются бесконечно большими в бесконечно
удаленной точке (доказать самостоятельно,
непосредственно используя определение
4.2). Их сумма
по теореме 4.2 также является бесконечно
большой в бесконечно удаленной точке
функцией. Функция
ограничена
в бесконечно удаленной точке, так как
при
имеем
и
.
По доказанному в
задаче 2 утверждению функция
является бесконечно большой в бесконечно
удаленной точке.
§ 5. Предел функции
В этом и последующих
§ 6, § 7, § 8 предполагается, что функция
задана на множестве
,
а точка
– точка сгущения этого множества. Если
же речь идет о бесконечно удаленной
точке, то предполагается, что эта точка
является предельной точкой множества
.
Определение 5.1.
Число
является
пределом функции
в точке
(в бесконечно удаленной точке),
если функцию
можно представить в виде
,
где
– функция, бесконечно малая в точке
(в бесконечно удаленной точке).
Тот факт, что число
является пределом функции
в точке
,
записывается следующим образом
(подстрочную запись
следует читать так: «при
,
стремящемся к
»).
Тот факт, что число
является пределом функции
в бесконечно удаленной точке,
записывается следующим образом
(подстрочную запись
следует читать так: «при
,
стремящемся к бесконечности»).
Так как
является бесконечно малой, можно
сформулировать определение предела в
другой, эквивалентной, форме.
Определение 5.2.
Число
является пределом
функции
в точке
(или при
,
стремящемся к
),
если для любого положительного числа
можно
указать такое положительное (зависящее
от
)
число
,
что для всех
выполнено неравенство:
(или выполнено
двойное неравенство (
)).
Определение 5.3.
Число
является пределом
функции
в бесконечно удаленной точке (или
при
,
стремящемся к бесконечности),
если для
любого положительного числа
найдется такое положительное (зависящее
от него) число
,
что для всех
справедливо неравенство
(или выполнено
двойное неравенство (
).
Замечание 5.1. В
определениях 5.1, 5.2, 5.3 речь идет о конечном
пределе функции
.
Если функция
является бесконечно
большой в точке
(или в бесконечно
удаленной точке),
то этот факт записывается следующим
образом:
(или
).
Замечание 5.2.
Если
– бесконечно большая в точке
функция и в некоторой окрестности
(
)
сохраняется неравенство
,
то пишут
,
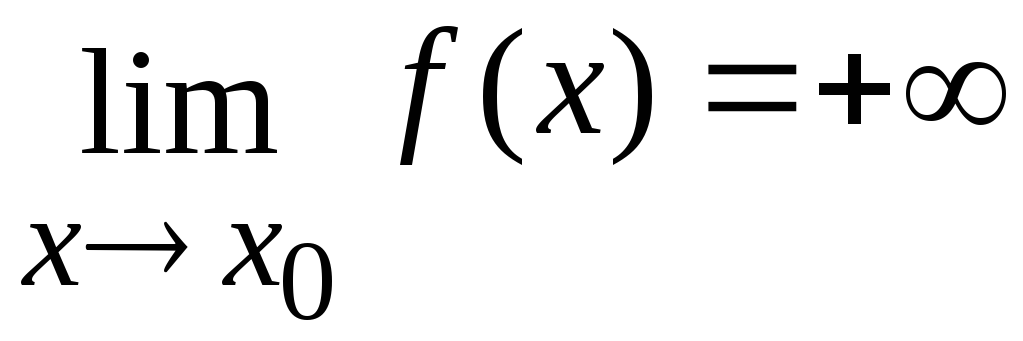если сохраняется
неравенство
,
то пишут
.
Аналогичную
форму записи используют для случая
бесконечно удаленной точки. Если для
всех
,
удовлетворяющих условию
(
),
сохраняется неравенство
,
то пишут
.
Если для всех
,
удовлетворяющих условию
(
),
сохраняется неравенство
,
то пишут
.