Вычисление пределов степенно-показательных функций

Пусть функции и заданы на множестве и функция на нем положительна. Функция

называется степенно - показательной.

Предположим, что – точка сгущения множества и существуют конечные пределы

, ,

где . Нужно найти

.

Воспользовавшись тождествами , запишем исходное выражение в виде

.

В силу теоремы 6.1 получим

.

При заданных значениях пределов будем иметь

.

Из проведенного рассуждения видно, что предположение о существовании конечных пределов и можно отбросить. Действительно, для нахождения предела выражения достаточно знать предел произведения (конечный или бесконечный).

1) Пусть . Тогда .

2) Если , то .

3) Если , то .

Заметим, что произведение может оказаться неопределенностью типа . Тогда и исходное выражение представляет собой неопределенность. Перечислим возникающие здесь неопределенности.

1) Если , то вычисление предела приводит к неопределенности типа .

2) Если , то вычисление предела приводит к неопределенности типа .

3) Если , то вычисление предела приводит к неопределенности типа .

Во всех указанных случаях (, , ) можно раскрыть неопределенность в показателе степени, преобразуя ее к типу и используя соответствующие эквивалентные бесконечно малые.

Замечание 8.3. Приведенные выше рассуждения справедливы и для вычисления предела степенно-показательной функции в бесконечно удаленной точке: .

Пример 8.2. Вычислить .

Решение. Здесь , , поэтому имеем неопределенность типа . Преобразуем выражение под знаком предела:

.

В показателе степени имеем неопределенность типа . Заменой при на эквивалентную бесконечно малую раскрываем ее:

.

Таким образом,

.

Замечание 8.4. Аналогично доказывается равенство .

Пределы

,

образуют две формы одного и того же равенства, которое также является замечательным пределом и часто служат определением числа .

Задачи к §8

Задача 1. Вычислить .

Решение. Здесь имеем неопределенность типа . Преобразуем числитель дроби к форме произведения:

.

Затем заменим бесконечно малую в точке функцию эквивалентной бесконечно малой .

Тогда получим

.

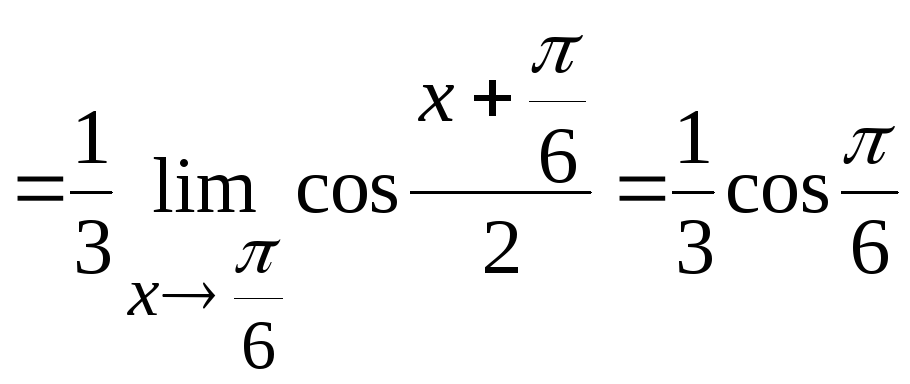Ответ: .

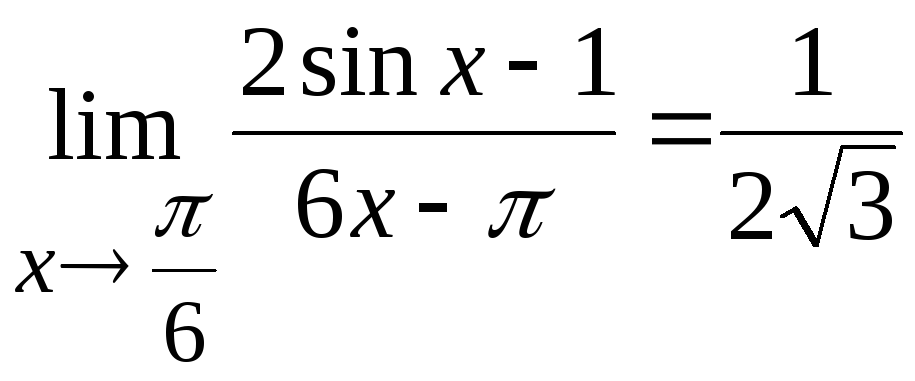Задача 2. Вычислить .

Решение. Здесь возникает неопределенность типа . Преобразуем знаменатель, воспользовавшись свойствами логарифмической функции, и выделим в аргументе логарифма слагаемое, равное 1:

.

Заменим бесконечно малую в точке функцию эквивалентной бесконечно малой . Числитель разложим на множители:

.

Тогда получим:

.

Ответ: .

Задача 3. Вычислить .

Решение. Здесь возникает неопределенность типа . Представим числитель в виде:

.

Затем заменим его эквивалентной бесконечно малой в точке функцией .

Функцию в точке тоже заменим на эквивалентную бесконечно малую .

Тогда

.

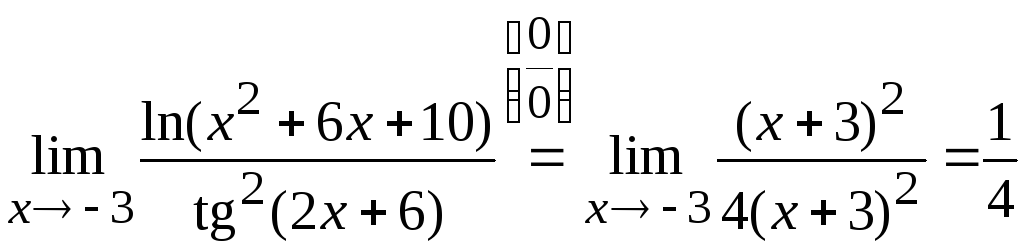Ответ: .

Задача 4. Вычислить .

Решение. Здесь возникает неопределенность типа . Представим числитель в виде:

.

Затем заменим его эквивалентной бесконечно малой в точке функцией .

Преобразуем знаменатель:

и заменим его на эквивалентную бесконечно малую . Тогда получим

.

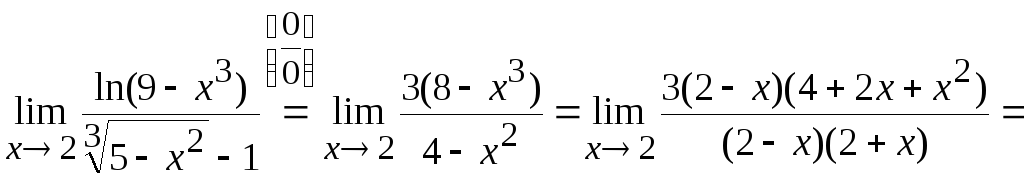
Ответ: .

Задача 5. Вычислить .

Решение. Здесь возникает неопределенность типа . Числитель можно заменить эквивалентной бесконечно малой .

Чтобы воспользоваться соотношением (8.4), преобразуем знаменатель:

и заменим его эквивалентной бесконечно малой .

Тогда

.

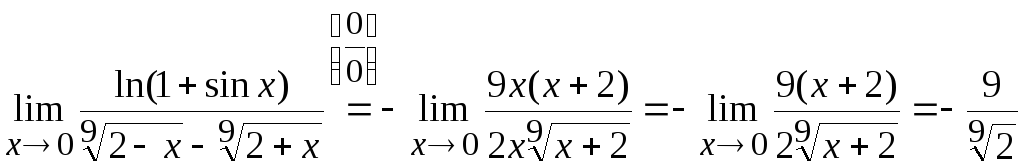Ответ: .

Задача 6. Вычислить .

Решение. Здесь имеем неопределенность типа . Чтобы применить к выражению соотношение (8.3), представим его в виде:

,

и заменим бесконечно малую функцию эквивалентной бесконечно малой . Знаменатель же представим в виде:

и, используя соотношения (8.2) и (8.8), заменим его эквивалентной бесконечно малой . Учитывая проведенные выкладки и соотношение (8.4), получим:

.

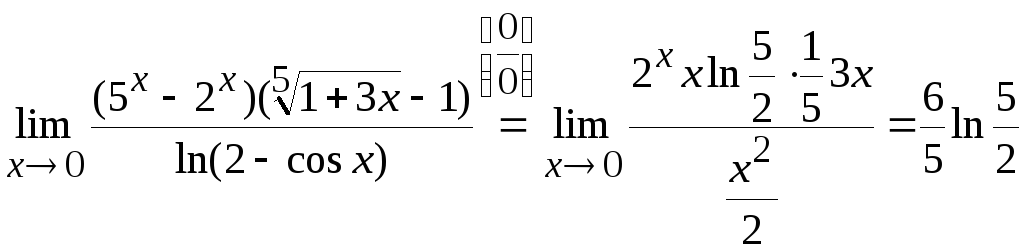Ответ: .

Задача 7. Вычислить .

Решение. Здесь имеем неопределенность типа . Используя ряд приемов, примененных в задачах 1–7, получим

.

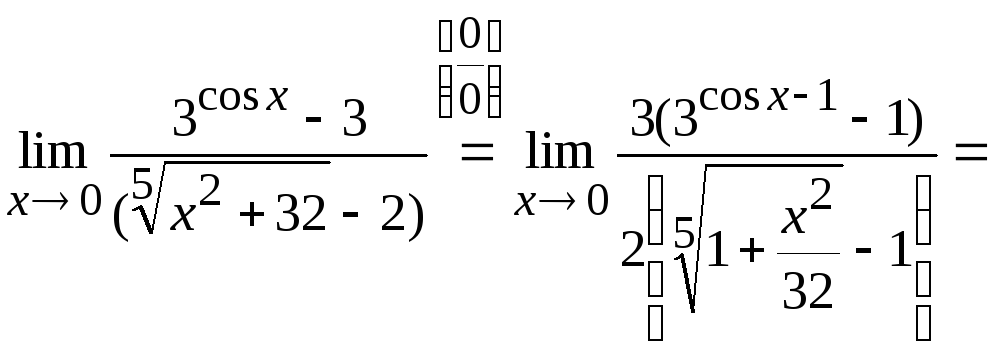
Ответ: .

Задача 8. Вычислить .

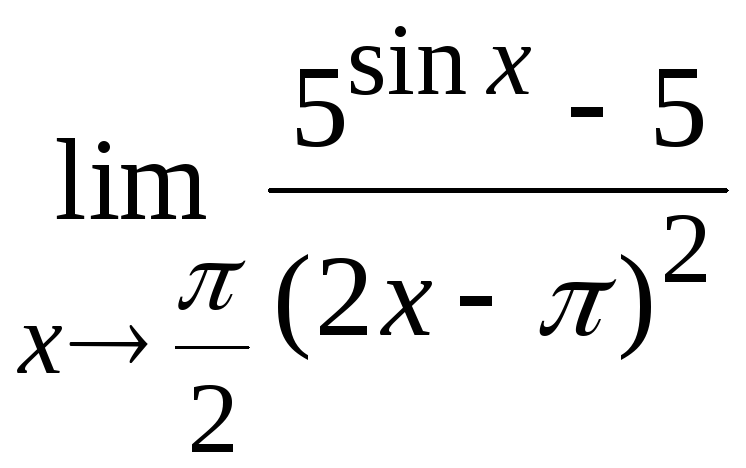Решение. Здесь имеем неопределенность типа . Используя ряд приемов, примененных в задачах 1–7 и формулы приведения для тригонометрических функций, получим

.

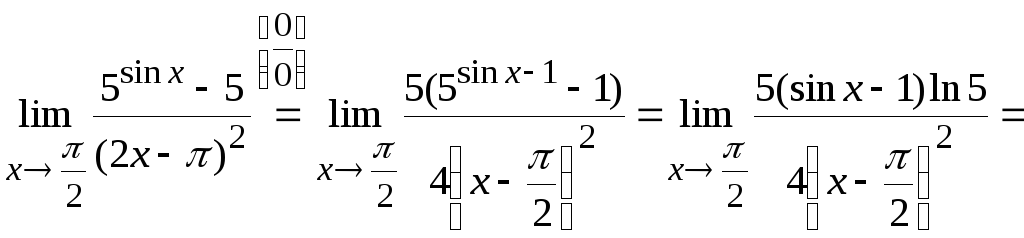
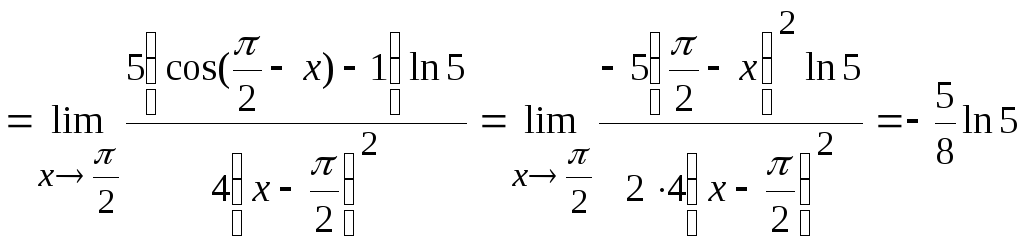Ответ: .

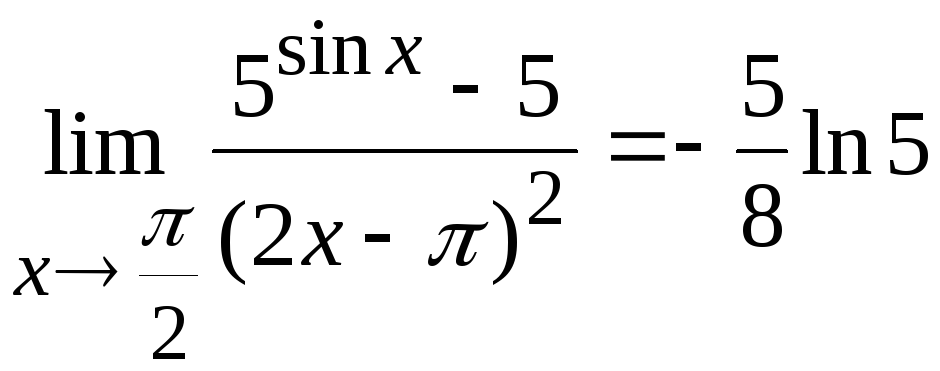Задача 9. Вычислить .

Решение. Здесь имеем неопределенность типа . Чтобы применить к числителю соотношение (8.2), преобразуем его следующим образом:

.

Теперь числитель согласно соотношению (8.2) можно заменить эквивалентной бесконечно малой .

Преобразуем знаменатель

.

Заменяем, используя соотношение (8.1), эквивалентной бесконечно малой .

Тогда

.

Ответ: .

Задача 10. Вычислить .

Решение. Здесь имеем неопределенность типа . Используя приемы, описанные выше, получим

.

.

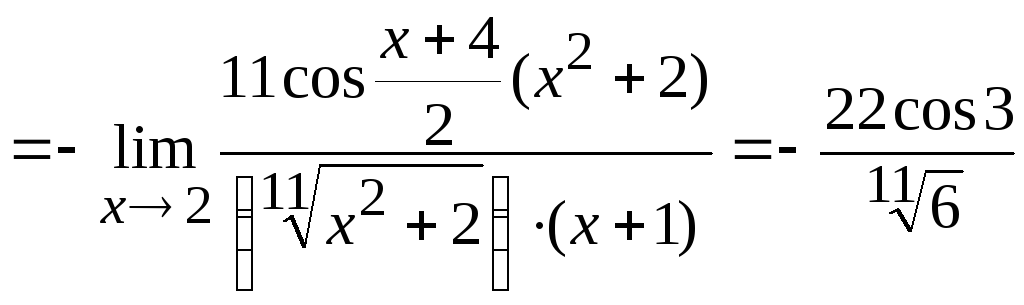Ответ: .

Задача 11. Вычислить .

Решение. Здесь имеем неопределенность типа . Используя теоремы 6.2 и 6.1, получим

.

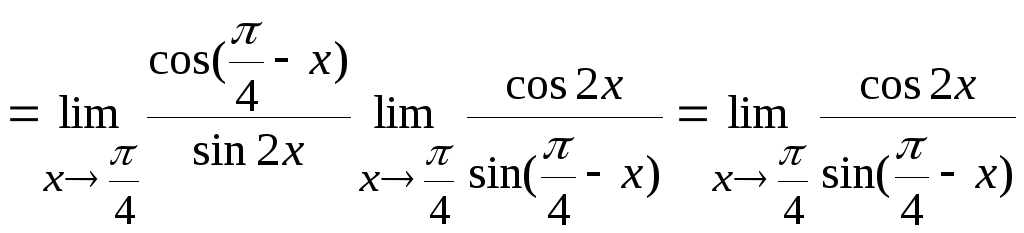Получили неопределенность типа . Преобразуем выражение с помощью формул приведения, затем переходим к эквивалентным бесконечно малым. В итоге получим

.

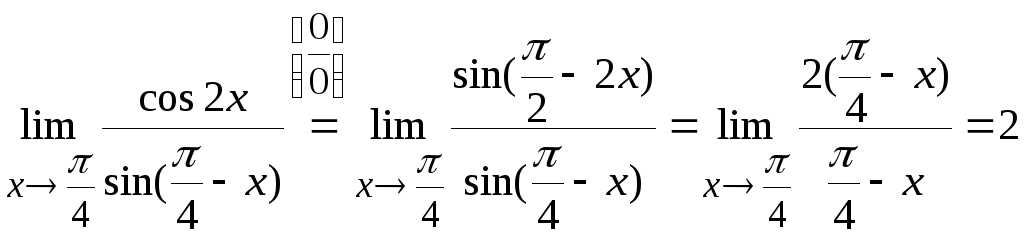Ответ: .

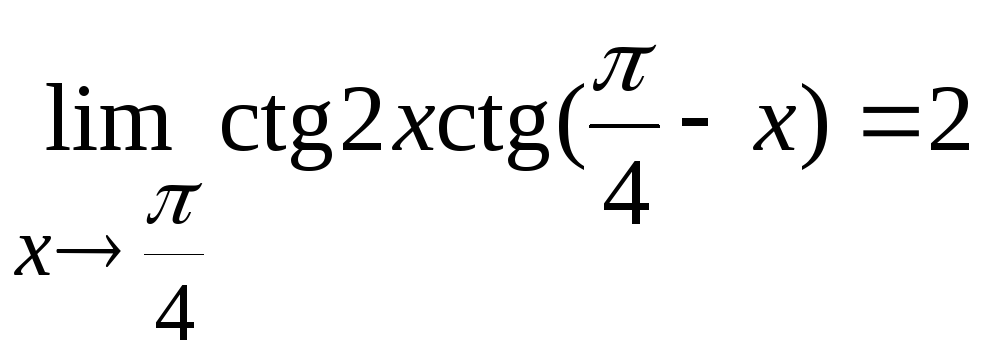Задача 12. Вычислить .

Решение. Здесь имеем неопределенность типа . Выделим в основании степени:

.

Заметим, что при .

Справедлива цепочка равенств

.

Заменяя логарифм эквивалентной бесконечно малой согласно соотношению (8.2) и используя замечание 6.4 для раскрытия неопределенности, получим

.

Ответ: .

Задача 13⁴. Вычислить .

Решение. Здесь имеем неопределенность типа . Введем переменную . Если , то .

.

Выделим в основании степени:

,

тогда

.

Заметим, что при . Заменим функцию эквивалентной бесконечно малой , будем иметь

.

Используя теорему 7.3, окончательно получим

.

Ответ: .

Задача 14. Вычислить .

Решение. Здесь возникает неопределенность типа . Поскольку

,

вычислим сначала . Мы имеем дело с неопределенностью типа .

Воспользовавшись последовательно соотношениями (8.2) и (8.1), будем иметь

.

Ответ: .

Задача 15. Вычислить .

Решение. Здесь возникает неопределенность типа . Воспользуемся формулой

.

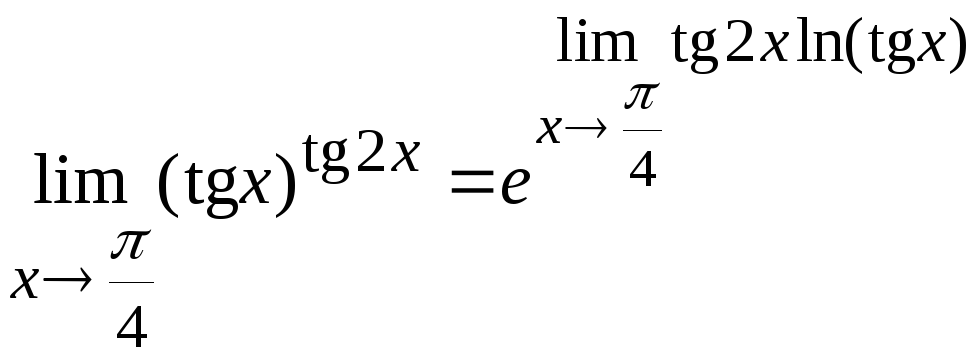Вычислим предел, стоящий в показателе степени. Для этого требуется раскрыть неопределенность типа . Преобразуем ее в неопределенность типа и воспользуемся эквивалентностью бесконечно малых:

.

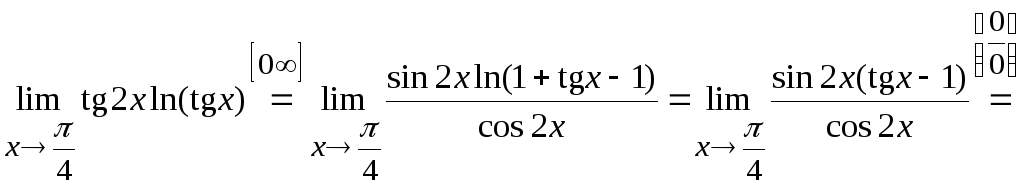
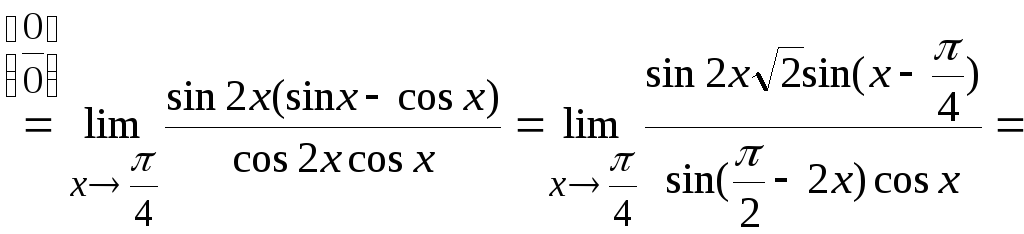
Ответ: .

Задача 16. Вычислить .

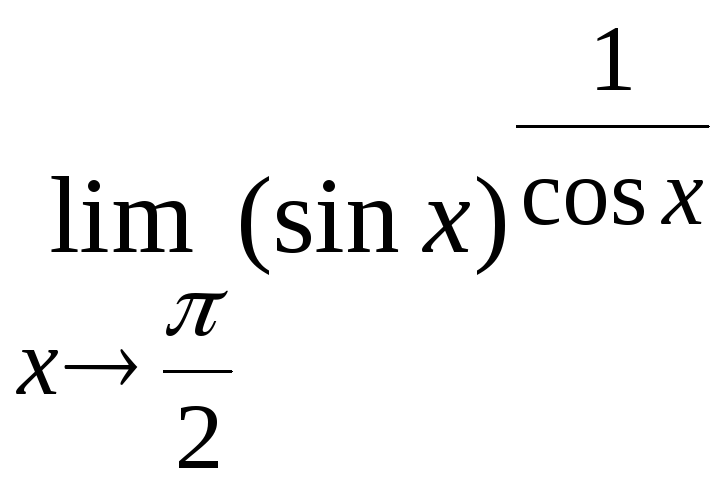Решение. Здесь возникает неопределенность типа . Преобразуем исходное предельное выражение

.

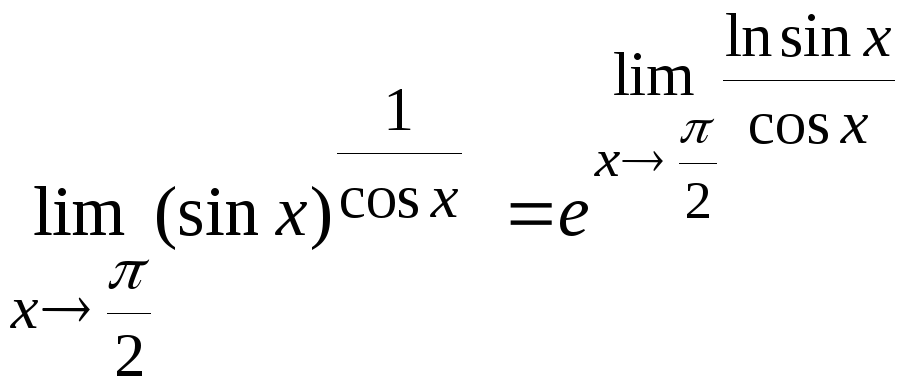Вычислим предел, стоящий в показателе степени.

.

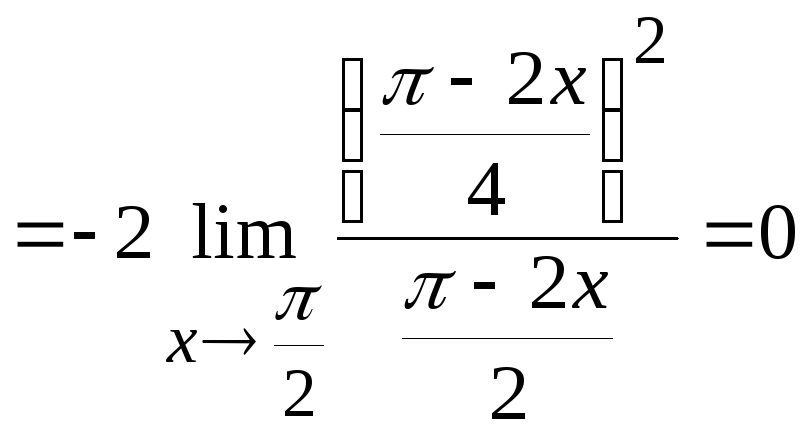Ответ: .