Свойства функций, непрерывных на замкнутом промежутке
Отметим свойства непрерывных функций, важные для нас в дальнейшем.
Теорема 9.3 (без
доказательства).
Если функция
непрерывна на замкнутом промежутке
,
то она достигает на нем своего наибольшего
(
)
и наименьшего
(
)
значений.
Эти значения могут достигаться как внутри промежутка, так и на любом из его концов.
Теорема 9.4 (без
доказательства). Если
функция
непрерывна на замкнутом промежутке
,
то она достигает на нем всех значений,
лежащих между своим наибольшим (
)
и наименьшим (
)
значениями.
Теоремы проиллюстрированы рис. 9.3 и 9.4.
Рис. 9.3. Рис. 9.4.
Задачи к §9
Задача 1. Указать точки, в которых перечисленные ниже функции терпят разрыв, и определить тип разрыва:
а)
б)
в)
г)
д)
Решение.
а) функция
на каждом из интервалов своего задания
является непрерывной. Она может терпеть
разрыв лишь в точках
и
,
в которых изменяется формула, определяющая
функцию. Для исследования функции
в указанных точках вычислим и сравним
в них пределы слева и справа.
Рассмотрим точку
.
Вычислим в ней односторонние пределы:
,
.
Пределы функции
в точке
слева и справа равны. Следовательно,
.
Поскольку
,
функция
непрерывна в точке
.
Рассмотрим точку
:
,
.
Оба предела функции
в точке
существуют, но они не равны друг другу.
Следовательно, в этой точке функция
терпит разрыв I
рода.
Ответ:
в точке
функция
терпит разрыв I
рода, во всех остальных точках
она непрерывна.
б) Функция
определена для всех
.
В точке
не существует конечного предела слева:
.
Ответ:
функция
непрерывна во всех точках
,
кроме точки
,
где она терпит разрыв II
рода.
в) Функция
определена для всех
.
Раскрывая по определению модуль, получим:
,
при
;
,
при
.
Следовательно,
,
.
В точке
функция
имеет разрыв I
рода.
Ответ:
функция
непрерывна во всех точках
,
кроме точки
,
где она терпит разрыв I
рода.
г) Функция
определена для всех
.
Она может терпеть разрыв лишь при
.
Вычислим в ней односторонние пределы:
,
.
Они существуют,
но не равны друг другу. Следовательно,
в точке
функция
имеет разрыв I
рода.
Ответ:
функция
непрерывна во всех точках
,
кроме точки
,
где она терпит разрыв I
рода.
д) Функция
определена для всех
.
Она может терпеть разрыв лишь при
.
Предел слева в этой точке:
,
так как
.
При вычислении предела справа учтем,
что
.
Тогда
.
Следовательно, в
точке
функция
имеет разрыв I
рода.
Ответ:
функция
непрерывна во всех точках
,
кроме точки
,
где она терпит разрыв I
рода.
Задача 2.
Функция
определена для всех
,
кроме точки
.
Доопределить ее в точке
так, чтобы новая функция
была непрерывна при всех значениях
:
а)
при
;
б)
Решение.
а) Функция
не определена при
.
Вычислим предел функции в этой точке,
заменяя
на эквивалентную бесконечно малую.
Получим:
.
Чтобы новая функция
была непрерывна в точке
,
в этой точке следует назначить ей
значение
.
Ответ:
б) Функция
не определена при
.
Вычислим ее пределы слева и справа в
этой точке. Используя соотношения (8.4)
и (8.3) для замены на эквивалентные
бесконечно малые функции, получим:
,
.
Следовательно, по
теореме 5.1 в точке
существует предел:
.
Именно этим числом следует доопределить
функцию так, чтобы новая функция
была непрерывна в точке
.
Ответ:
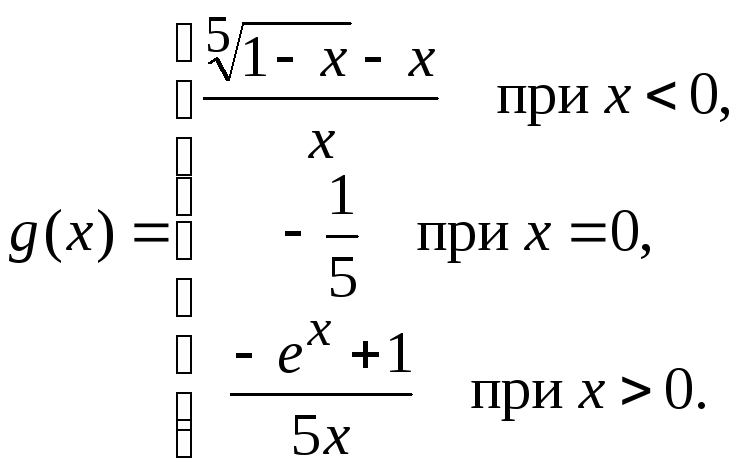
Задача 3.
Функция
определена следующим образом:
Найти значения
параметров
и
так, чтобы функция
была непрерывна для всех
.
Решение.
Функция
на каждом из интервалов своего задания
является непрерывной. Она может терпеть
разрыв лишь в точках
и
,
в которых изменяется формула, определяющая
функцию. Вычислим пределы слева и справа
в этих точках и приравняем их:
,
,
,
.
Следовательно,
значения
и
должны удовлетворять системе
имеющей решение
,
.
Ответ:
