Задачи к §3

Задача 1. Доказать, что функция является бесконечно малой в точке при любых значениях числа .

Решение. Заметим, что функция определена для всех и для всех выполнено неравенство . Таким образом, функция локально ограничена при .

Согласно замечанию 2.3 функция при является бесконечно малой в точке .

В силу теоремы 3.3 функция является бесконечно малой в точке как произведение бесконечно малой на локально ограниченную в этой точке функцию .

Задача 2. Доказать, что функция является бесконечно малой в точке .

Решение. Функция определена для всех . Преобразуем ее:

.

Функция является бесконечно малой в точке функцией, а функция локально ограничена в ней. Следовательно, по теореме 3.3 функция является бесконечно малой в точке функцией как произведение бесконечно малой на локально ограниченную в этой точке функцию.

Задача 3. Доказать, что функция является бесконечно малой в точке .

Решение. Преобразуем функцию к виду:

.

Функция удовлетворяет неравенству: . Если же , то . Таким образом, функция локально ограничена в точке . Функции является бесконечно малой в точке . Следовательно, по теореме 3.3 функция является бесконечно малой в точке функцией как произведение бесконечно малой на локально ограниченную в этой точке функцию.

Задача 4. Доказать, что функция 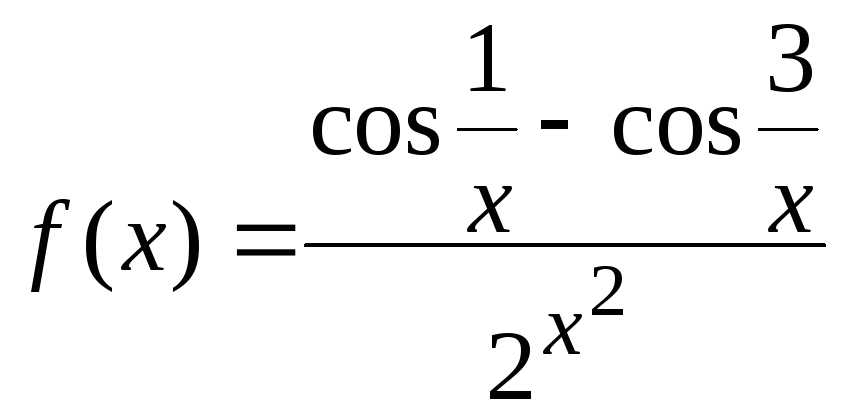является бесконечно малой в бесконечно удаленной точке.

Решение. Преобразуем функцию к форме произведения:

.

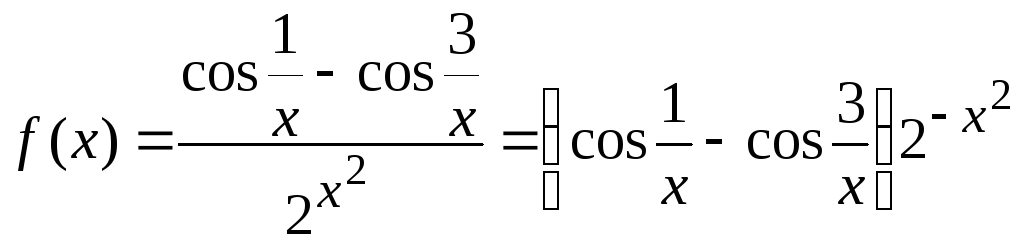Функция является бесконечно малой в бесконечно удаленной точке. Действительно, задавшись произвольным , укажем по нему . Тогда при получим , откуда . Функция локально ограничена в бесконечно удаленной точке, поскольку при справедливо . В силу теоремы 3.4 функция является бесконечно малой в бесконечно удаленной точке функцией как произведение бесконечно малой в бесконечно удаленной точке на ограниченную функцию .

§ 4. Бесконечно большие функции

Определение 4.1. Пусть функция задана на множестве , и точка – точка сгущения этого множества. Функция называется бесконечно большой в точке , если для любого можно указать такое , что для всех справедливо неравенство:

.

Пример 4.1. Функция является бесконечно большой в точке . Действительно, для произвольного можно выбрать . Тогда, если , то .

Геометрический смысл определения 4.1 проиллюстрирован рисунком 4.1.

Рис. 4.1.

Определение 4.2. Пусть функция задана на множестве и бесконечно удаленная точка является предельной точкой множества . Функция называется бесконечно большой в бесконечно удаленной точке, если для любого положительного числа найдется такое положительное число , что для всех справедливо неравенство

.

Пример 4.2. Функция является бесконечно большой в бесконечно удаленной точке. Зададимся произвольным числом и укажем . Тогда при будет выполнено , откуда .

На рис. 4.2 проиллюстрирован выбор по заданному для бесконечно большой в бесконечно удаленной точке функции .

Рис. 4.2.

Теорема 4.1. Пусть функции , заданы на множестве и точка – точка сгущения этого множества. Пусть

(или ).

Тогда

1. если – бесконечно малая в точке функция, то – бесконечно большая в этой точке функция;

2. если – бесконечно большая в точке функция, то – бесконечно малая в этой точке функция.

Доказательство. 1. Выберем произвольное число и укажем по нему . Для существует такое , что для всех будет выполнено неравенство . Тогда для всех будут выполнены соотношения

.

Тем самым доказано, что – бесконечно большая в точке функция.

2. Выберем произвольное число и укажем по нему (). Для существует такое , что для всех будет выполнено неравенство . Тогда для всех будут выполнены соотношения

.

Тем самым доказано, что – бесконечно малая в точке функция.

Теорема 4.2. Пусть функции , заданы на множестве с точкой сгущения и являются бесконечно большими в этой точке. Если в некоторой окрестности точки , то их сумма также является бесконечно большой функцией в точке .

Доказательство. Выберем произвольное число и для значения найдем такие , , что будут выполнены неравенства

при ,

при .

Пусть . Очевидно, . Указано такое , что для всех выполнены оба неравенства, откуда с учетом условия , получим:

.

В силу произвольности доказано, что является бесконечно большой в точке .

Замечание 4.1. Теоремы 4.1 и 4.2, сформулированные для точки , можно переформулировать и для бесконечно удаленной точки.

Пример 4.3. Функция по теореме 4.2 является бесконечно большой в бесконечно удаленной точке функцией как сумма двух бесконечно больших функций: и (см. пример 4.2) .

Замечание 4.2. Теорема 4.2 утверждает, что сумма двух бесконечно больших в точке функций одинакового знака является бесконечно большой функцией в этой точке. Таким же образом можно показать, что произведение двух бесконечно больших в точке функций является бесконечно большой в этой точке функцией (доказательство провести самостоятельно).