ЗМІСТ

.

5 Аксонометричні проекції 4

1. Загальні відомості 4

2. Різновиди аксонометричних проекцій 5

1. Прямокутна ізометрія 6

2. Прямокутна діметрія 6

3. Косокутна фронтальна діметрія 7

5.3 Аксонометричні проекції плоских фігур 8

1. Побудова прямокутника 8

2. Побудова шестикутника 9

3. Побудова п'ятикутника 9

4. Побудова аксонометричних проекцій кіл 11

5.4 Аксонометричні проекції поверхонь та об'єктів 16

1. Побудова гранних поверхонь 16

2. Побудова аксонометрії сфери 17

3. Побудова аксонометрії об'єкта 18

5.5 Аксонометричні проекції технічних деталей 18

1. Загальні положення 18

2. Нанесення лінії штриховий вирізів 19

3. Умовності та спрощення в аксонометрії 20

4. Побудова аксонометричних проекцій технічної деталі та приклади для закріплення 21

6. Методичні рекомендації до виконання графічного завдання з теми «Аксонометрія» 25

7. Практичне використання 27

8. Питання, вправи та завдання до самостійної підготовки студентів 27

Додаток 1 28

Додаток 2 29

Додаток 3 30

Перелік літератури 44

5 Аксонометричні проекції

5.1. Загальні відомості

Метод прямокутнього проекціювання має багато переваг. Одна з них — зображення проекціюється на площину невикривленим. Завдяки цьому комплексне креслення будується досить просто, за ним легко визна­чити розміри деталі та виготовити її. Однак існує суттєвий недолік: зображення не досить наочні.

Одночасне розглядання двох, трьох і більше зображень створює труднощі в уяв­ленні просторового об'єкта. Тому досить часто при ви­ко­нан­ні технічних креслень необ­хідно поруч із зображенням деталей в системі ортогональних проекцій мати зображення більш наочні. Для побу­до­ви таких зображень і використовуються аксонометричні проекції. Слово "аксонометрія" походить від грецьких слів axon (вісь) і metreo (вимірюю), що разом означає вимірювання по осях. Аксонометричною проек­цією називається зображення, що утворюється шляхом проекціювання паралельними променями предмета, разом з прямокутними осями коор­ди­нат (X, Y, Z), до яких він віднесений, на довільно розміщену площину Р, яка називається площиною аксоно­мет­рич­них проекцій (або картинною площиною) рис. 1. Отримані у такий спо­сі­б про­екції осей X`,Y`,Z нази­ва­ються аксонометричними осями.

На осях X, Y, Z відкладено відрізки а, b, c, які прийнято за одиниці виміру вздовж цих осей. Відрізки a`, b`, c` на аксонометричних осях являють собою проекції відрізків а, b, c. Вони є одиницями виміру по аксонометричних осях. Відношення k = a`/a; m = b`/b; n = c`/c нази­ва­ються коефіцієнтами (або показниками) спотворення по аксоно­метричних осях.

Р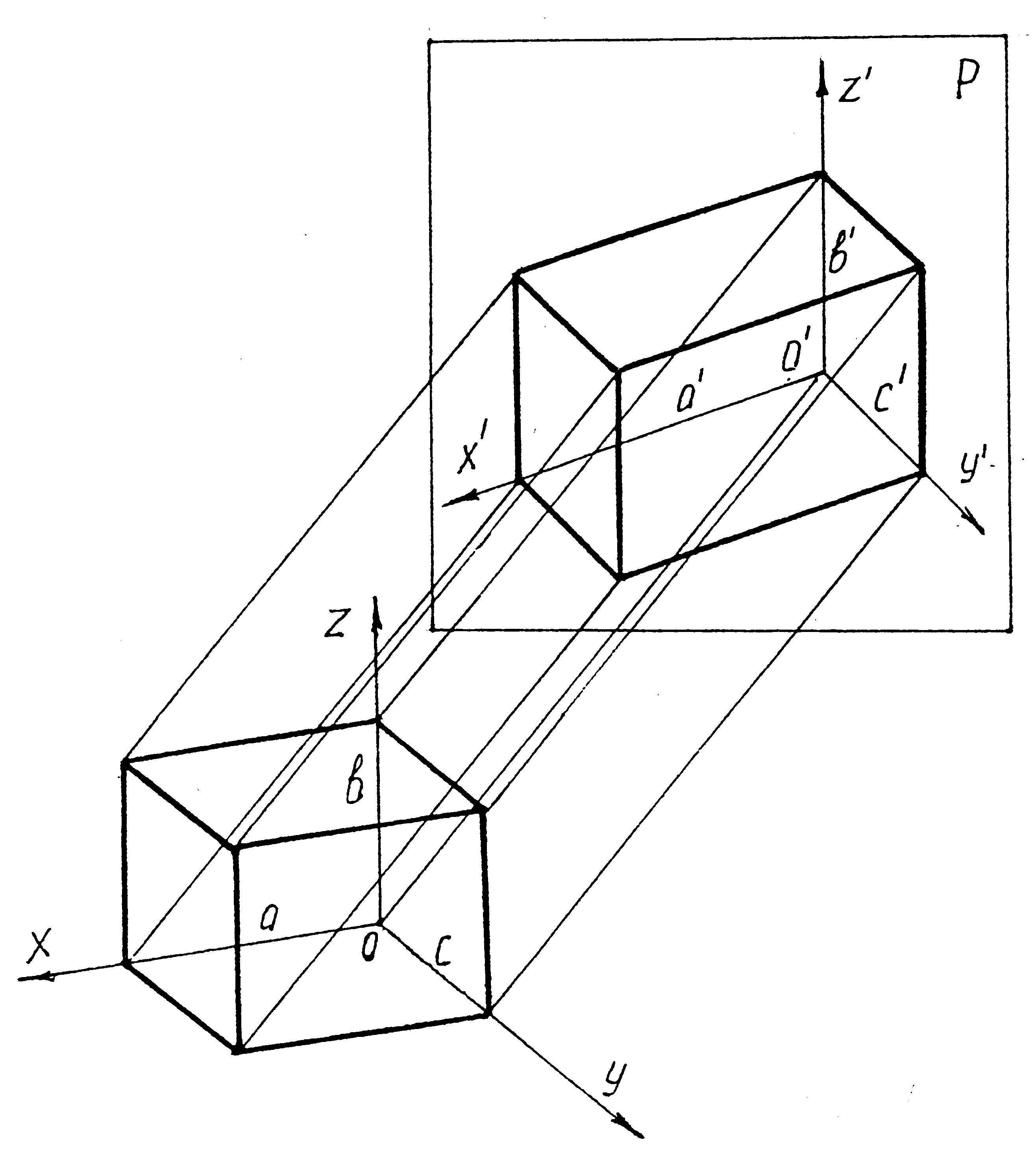 исунок 1

5.2. Різновиди аксонометричних проекцій

В залежності від розміщення координатних осей по відношенню до картинної площини і від напрямку проекціюючих променів аксоно­мет­ричні проекції поділяються на декілька видів.

1. Якщо всі три показники викривлення по осях між собою не рівні, (к = m = n), то проекція називається триметричною.

2. Якщо два показники викривлення рівні (наприклад k = n), а третій відмінний від них, то проекція називається диметричною.

3. І якщо всі три показники викривлення по осях рівні (k = m = n), то проекція називається ізометричною.

Зі всіх видів аксонометричних проекцій ГОСТ 2.317–69 рекомендує такі, які мен­ше викривляють вид предмета та найбільш зручні для користування — це прямокутна ізо­­метрія, прямокутна диметрія та косокутна фронтальна диметрія. Розрізняються вони в залежності від того, який кут утворюють проекціюючі промені з площиною проекцій. Якщо проекціюючі промені перпендикулярні до картинної площини, проекції назива­ють­ся прямокутними. Якщо ці промені неперпендикулярні до тієї ж площини, проекції на­зиваються косокутними.

5.2.1. Прямокутна ізометрія

Саме слово "ізометрія" означає однаковий вимір. Координатні осі в ізометрії роз­міщу­ються по відношенню до картинної площини з одна­ко­вим нахилом, а напрямок проекціювання прямокутний. Аксоно­мет­ричні осі при цьому утворюють між собою кут 120° (Рис. 2, а).

Дійсні коефіцієнти викривлення по осях дорівнюють 0,82 (k = m = n = 0,82), але оскільки вони незручні для підрахунку розмірів при побудові наочних зображень, їх замінюють більш зручними приведеними коефіцієнтами, які дорівнюють 1 (k = m = n = 1). При цьому зображення збільшується в 1,22 рази. На рис. 2, б показано, як побудувати осі ізометрії за допомогою кутника з кутами 30°, 60° і 90°. На рис. 2, в — за допомогою циркуля.

Р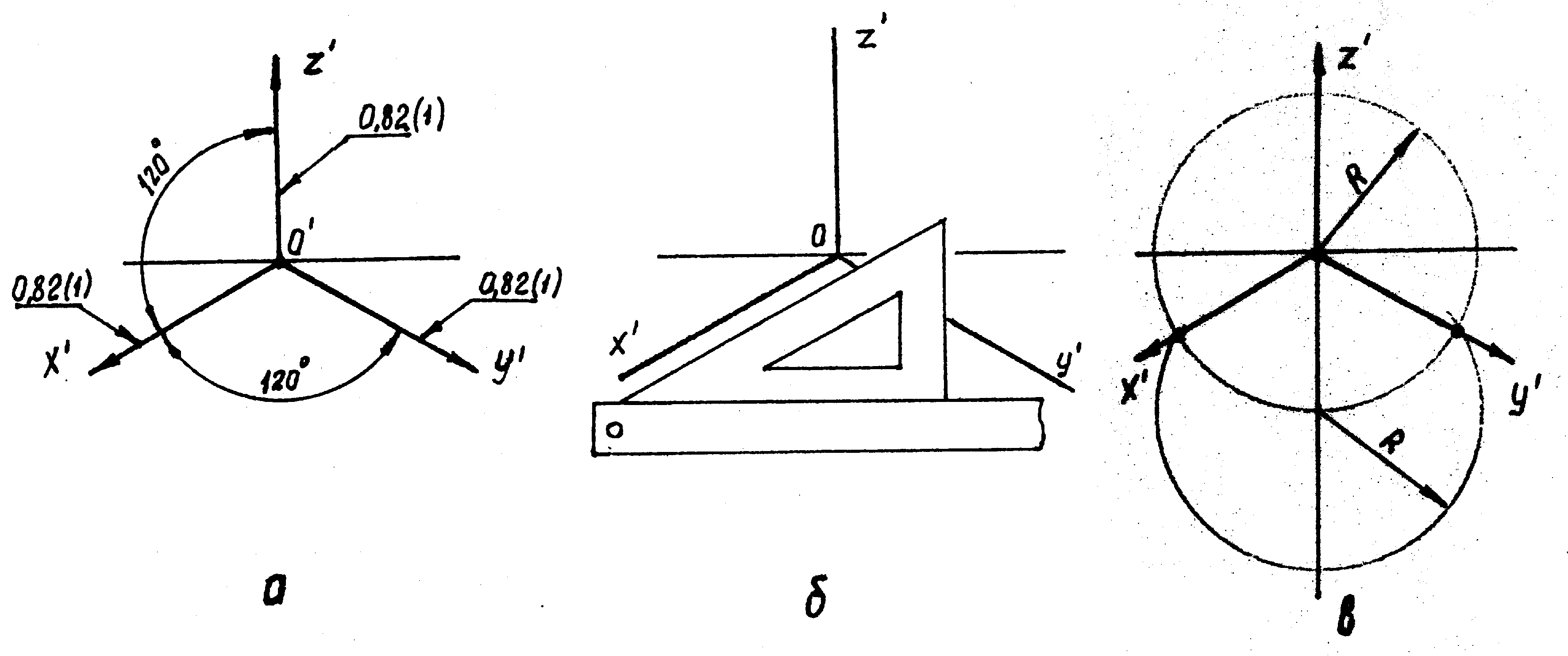 исунок 2