Решение задач

7.4. Тонкий однородный стержень АВ массы движется поступательно с ускорением под действием сил и (рис.58). Найти длину стержня, если расстояние между точками приложения сил равно .

Решение. По условию задачи стержень движется поступательно, поэтому момент внешних сил, действующих на стержень относительно любой оси равен нулю. Выберем в качестве оси ось, проходящую через центр масс (точка С на рис.58), и направленную перпендикулярно плоскости рисунка, тогда

.

Центр масс любой системы частиц движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы. Запишем уравнение движения центра масс стержня в проекциях на ось X:

.

Решая совместно записанные уравнения, получим искомую величину:

.

7.5. На однородный сплошной цилиндр массы M и радиуса R плотно намотана лёгкая нить, к концу которой прикреплён груз m. В момент t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени:

а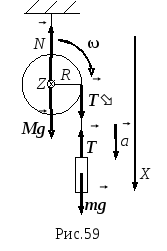) модуля угловой скорости цилиндра;

б) кинетической энергии всей системы.

Решение. а) Система состоит из двух тел (рис.59): груза массы m, движущегося поступательно вдоль оси X, и цилиндра массы M, вращающегося относительно оси Z, проходящей через ось цилиндра, перпендикулярно плоскости рисунка «от нас» (значок на рис.59).

На груз действует сила тяжести и сила натяжения нити . Составим уравнение движения груза в проекциях на ось X

. (1)

На цилиндр действуют сила тяжести , сила реакции крепления и сила натяжения нити . Вращающий момент относительно оси Z создаёт только сила натяжения нити (поскольку только у этой силы есть плечо относительно оси Z). Составим уравнение движения цилиндра относительно оси Z:

. (2)

Момент инерции цилиндра

. (3)

Невесомость нити позволяет считать силу натяжения вдоль всей нити постоянной по модулю

. (4)

Если нить не проскальзывает относительно цилиндра, то касательное ускорение его точек, соприкасающихся с нитью, равно ускорению нити в любой ее точке, а, следовательно, и ускорению груза

. (5)

Угловая скорость цилиндра (см. раздел I) равна

. (6)

Решая систему из уравнений (1)-(6) получим выражения для угловой скорости цилиндра

.

б) Кинетическая энергия системы складывается из энергии поступательно движущегося груза и энергии вращающегося цилиндра

.

Учитывая, что , найдём кинетическую энергию системы

.

7.6. Однородный цилиндр скатывается без скольжения по наклонной плоскости, составляющей угол с горизонтом. Найти ускорение цилиндра.

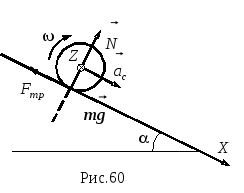Решение: Направим ось X вдоль наклонной плоскости вниз, а ось Z - перпендикулярно плоскости чертежа, проходящей через центр масс цилиндра (значок на рис.60). Цилиндр совершает плоское движение – поступательное (вдоль оси X) и вращательное (относительно оси Z).

Покажем силы, действующие на цилиндр при его движении вниз. На цилиндр действуют сила тяжести , а со стороны поверхности в нормальном направлении - сила нормальной реакции опоры и против направления движения - сила трения (рис.60). Поскольку проскальзывания нет, сила трения является силой трения покоя.

Уравнение поступательного движения цилиндра в проекциях на оси X имеет вид

,

Уравнение вращательного движения цилиндра относительно оси Z, проходящей через центр цилиндра:

,

где - момент инерции цилиндра относительно оси вращения, - угловое ускорение цилиндра, - его радиус.

Условие отсутствия проскальзывания () приводит к уравнению

.

Решая систему записанных уравнений, найдем ускорение цилиндра

.

7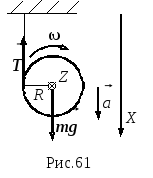.7. Однородный сплошной цилиндр массы m и радиуса R (рис.61) в момент t = 0 начинает опускаться под действием силы тяжести. Пренебрегая массой нити, найти угловое ускорение цилиндра.

Решение. Направим ось X вертикально вниз вдоль движения цилиндра, а ось Z - перпендикулярно плоскости чертежа, проходящей через центр масс цилиндра (значок на рис.61). Цилиндр совершает плоское движение – поступательное движение вдоль оси X и вращательное вокруг оси Z. Покажем силы, действующие на цилиндр при его движении вниз, это сила тяжести и сила натяжения нити . Запишем систему уравнений, описывающих движение цилиндра. Уравнение поступательного движения цилиндра в проекциях на ось X

,

где a - ускорение центра масс цилиндра.

Уравнение вращательного движения цилиндра относительно оси Z

где - момент инерции цилиндра относительно оси вращения, – угловое ускорение цилиндра, - его радиус.

Нить не проскальзывает, поэтому соотношение между кинематическими параметрами

.

Решив совместно записанные уравнения, получим угловое ускорение цилиндра:

.

7.8. Однородное кольцо радиуса R раскрутили до угловой скорости и осторожно положили на горизонтальную плоскость. Сколько времени кольцо будет вращаться на плоскости, если коэффициент трения равен .

Решение. Направим ось Z перпендикулярно горизонтальной плоскости, на которую положили кольцо (рис.62). Уравнение вращательного движения кольца относительно оси Z:

.

Выделим на кольце малый элемент массой и найдем момент силы трения этого элемента относительно оси Z:

.

Тогда момент силы трения кольца относительно этой оси равен

.

Учитывая, что момент инерции кольца относительно оси Z равен , уравнение вращательного движения примет вид:

,

.

В момент остановки кольца его угловая скорость равна нулю , поэтому, проинтегрировав левую часть уравнения от до 0, а правую от 0 до , получим

,

откуда выразим искомую величину:

.

Теперь усложним задачу и рассмотрим вращательное движение диска.

7.9*. Решить предыдущую задачу, только вместо кольца на горизонтальную плоскость положить раскрученный до угловой скорости однородный диск.

Решение. Уравнение вращательного движения диска относительно оси Z, направленной перпендикулярно плоскости вращения диска (рис.63):

.

Диск представим набором колец бесконечно малой толщины dr (рис.63). Каждое такое кольцо находится на расстоянии r от оси вращения Z, а его масса равна

.

Согласно результату предыдущей задачи момент силы трения каждого такого кольца равен

.

Учитывая, что момент инерции диска относительно оси Z равен , уравнение вращательного движения диска примет вид:

,

.

Проинтегрировав левую часть уравнения от до 0, а правую от 0 до , получим время вращения диска до его остановки

.