VI. Момент импульса. Законы изменения и сохранения момента импульса

1. Момент импульса материальной точки. Момент силы

М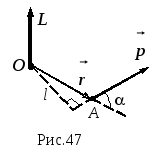оментом импульса материальной точки относительно точки 0 называют величину, определяемую векторным произведением

,

где - радиус-вектор материальной точки, проведенный из точки О, - ее импульс (рис.47). Направление вектора совпадает с направлением поступательного движения правого винта при его вращении от к .

Модуль момента импульса равен произведению импульса на плечо

,

где - плечо вектора .

Найдем производную по времени от момента импульса материальной точки относительно точки О

,

то есть она равна моменту результирующей силы относительно точки О (в силу параллельности векторов и их векторное произведение равно нулю =0). Модуль момента силы (рис.48) равен

,

где - плечо силы .

Выражение

есть закон изменения момента импульса материальной точки, часто называемого уравнением моментов.

В проекциях на некоторую на ось Z, проходящую через точку О уравнение моментов примет вид

.

Если тело участвует во вращении относительно этой оси, то уравнение моментов удобно записывать в проекциях на эту ось.

Решение задач

6.1. К точке А, радиус-вектор который относительно начала координат О равен , приложена сила , где a, b, A, B - постоянные, , , - орты осей X, Y и Z. Найти плечо l силы и ее момент относительно точки О.

Решение. По определению момент силы относительно точки О равен

.

Величину найдем, подставив значения и в исходную формулу

.

Направление вектора определим согласно правилу векторного произведения векторов (рис.49). Вектор момента силы перпендикулярен плоскости XY.

Модуль момента силы по определению равен:

,

где l - плечо силы. Плечо l силы относительно точки О равно

.

6 .2*. Небольшая шайба массы начинает скользить с вершины гладкой наклонной плоскости, высота которой и угол наклона к горизонту (рис.50). Найти модуль момента импульса шайбы относительно точки О через время после начала движения.

Решение. По определению момент импульса равен произведению импульса на плечо

.

Сначала найдем скорость движения шайбы, а потом, воспользовавшись определением, момент импульса шайбы.

Проанализируем силы, действующие на шайбу при ее движении вниз. На шайбу действуют сила тяжести и сила нормальной реакции опоры (рис.50). Направим ось X вдоль наклонной плоскости вниз (по ускорению), а ось Y - перпендикулярно плоскости вверх. Уравнение движения шайбы в проекциях на ось X примет вид

,

.

Поэтому скорость шайбы в момент времени (см. раздел I) равна

.

Тогда момент импульса шайбы относительно точки О равен

,

где - плечо силы, под действием которой движется шайба вдоль оси X, относительно точки О. Выразим длину плеча (рис.50) и определим модуль момента импульса шайбы относительно точки О

.

6.3. На массивный неподвижный блок радиуса R намотана легкая нерастяжимая нить, к свободному концу которой подвешено небольшое тело массы m. В момент t=0 систему предоставили самой себе, и она пришла в движение. Найти ее момент импульса относительно оси блока в зависимости от t.

Решение. Покажем силы, действующие на тела системы (рис.51). На блок действуют - сила тяжести , сила реакции крепления и сила натяжения нити , на груз - сила тяжести и сила натяжения нити . Вследствие невесомости нити .

Момент импульса системы относительно оси блока (ось Z на рисунке направлена от нас ) равен

,

где - суммарный момент сил системы относительно оси Z. Сила тяжести блока и сила реакции крепления проходят через ось Z, относительно которой мы ищем моменты этих сил, поэтому их моменты будут равны нулю. Силы натяжения нити и , равны по величине и противоположны по направлению и действуют вдоль одной прямой, поэтому их суммарный момент равен нулю. Момент импульса относительно оси Z имеет только сила тяжести груза . За промежуток времени dt момент импульса системы относительно оси Z получит приращение

,

где R - плечо силы тяжести относительно оси Z. Проинтегрировав левую часть полученного уравнения от 0 до , а правую от 0 до t, найдем момент импульса системы относительно оси Z в зависимости от t:

.