Для тел, взаимодействующих посредством консервативных сил, вводится понятие потенциальной энергии. В курсе механики рассматриваются два вида потенциальной энергии:

1. энергия тела в поле тяжести (если это поле однородное), равная 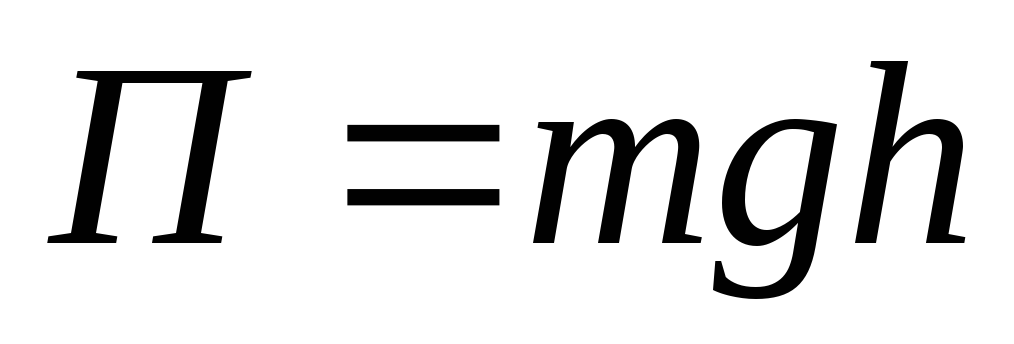, где h - высота, отсчитываемая от некоторого уровня, где потенциальная энергия принимается равной нулю. Поэтому при решении задач следует указать этот уровень,

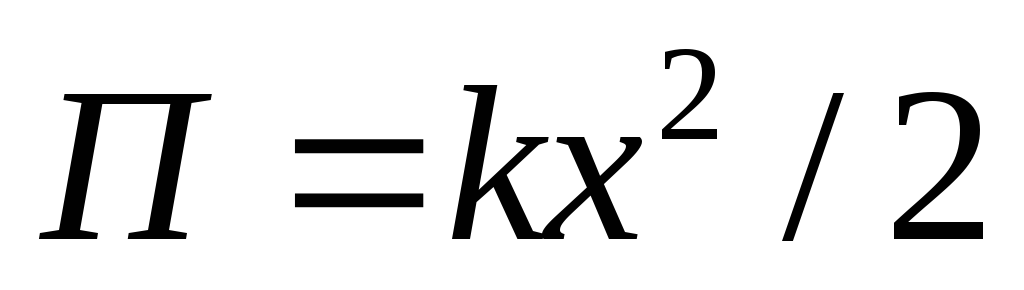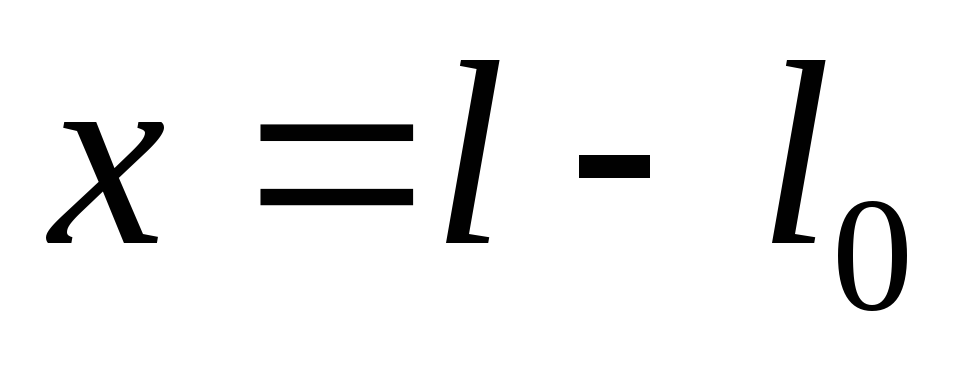2. энергия упругой деформации , где k - коэффициент жесткости пружины, x - ее растяжение (сжатие). Растяжение определяется как , где 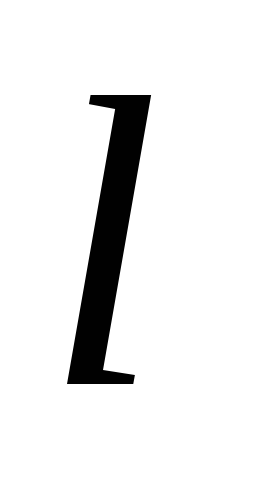- длина деформированной пружины, 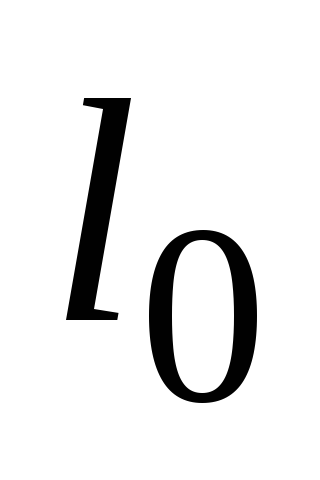- ее длина в недеформированном состоянии.

Потенциальная энергия изменяется за счет работы консервативных сил. Согласно закону об изменении потенциальной энергии

убыль потенциальной энергии системы равна работе консервативных сил, действующих на все частицы системы.

Решение задач

5.1. Частица совершает перемещение по некоторой траектории в плоскости XY из точки 1 с радиус-вектором в точку 2 с радиус-вектором . При этом на неё действовали некоторые силы, одна из которых . Найти работу, которую совершила сила . Здесь и - орты осей X и Y; , и определены в системе СИ.

Решение. Перемещение происходит под действием постоянной силы, для которой работа определяется как

,

подставив в которое и , получим

.

Тогда искомая работа силы равна

.

5.2. Небольшая муфточка массы m движется по гладкому проводу, изогнутому в горизонтальной плоскости в виде дуги окружности радиуса R (на рис.37 представлен вид сверху). В точке 1, где скорость муфточки , на неё начала действовать постоянная горизонтальная сила . Найти скорость муфточки в точке 2.

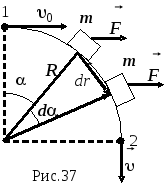Решение. Рассмотрим элементарное перемещение муфты , тогда элементарная работа силы на этом перемещении равна

,

так как (рис.37). Работа силы при перемещении муфточки из точки 1 в точку 2 равна

.

Согласно закону изменения кинетической энергии, приращение кинетической энергии равно работе всех сил, действующих на тело:

.

Из последнего выражения выразим скорость муфточки в точке 2

.

5.3. Брусок массы m находится на горизонтальной плоскости с коэффициентом трения . В некоторый момент ему сообщили начальную скорость . Найти среднюю мощность силы трения за всё время движения бруска .

Решение. По определению мощность - это работа, совершаемая силой за единицу времени:

,

средняя мощность

,

где A - работа, совершаемая силой за время .

Работа силы трения, действующей на брусок, определяется изменением его кинетической энергии от до . Поэтому на основании закона об изменении кинетической энергии

.

Брусок движется по горизонтальной плоскости под действием силы трения, поэтому его скорость в момент времени t определяется выражением

Запишем уравнение движения бруска (второй закон Ньютона) в проекциях на ось X, направленную вдоль его движения

.

Тогда

.

В момент остановки скорость бруска равна нулю . Поэтому время бруска до остановки равно

.

А искомая средняя мощность равна

.

5.4. В системе отсчёта, вращающейся вокруг неподвижной оси с постоянной угловой скоростью , перемещается небольшое тело из точки 1 в точку 2, которые расположены на расстояниях r₁ и r₂ от оси вращения (r₁ > r₂). Какую работу совершает при этом центробежная сила инерции?

Решение. Вращающаяся с постоянной угловой скоростью система отсчёта является неинерциальной. Поэтому на тело в такой системе отсчета действует центробежная сила инерции равная , где r - и есть расстояние от оси вращения. Работа этой силы по определению равна

.

Из полученного результата видно, что работа центробежной силы не зависит от траектории перемещения. Это значит, что центробежная сила является консервативной силой, а ее поле - потенциально.

5.5. Система состоит из двух последовательно соединённых пружин с жёсткостями k₁ и k₂. Найти минимальную работу, которую необходимо совершить, чтобы растянуть эту систему на .

Решение. Работа консервативных сил, действующих на систему, равна убыли потенциальной энергии:

.

Пружину растягивает внешняя неконсервативная сила, величина которой, согласно третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости, которая является консервативной. Поэтому работа внешней силы равна

.

Работа эта будет минимальна, если растяжение совершается достаточно медленно, так чтобы система в любой момент времени находилась в равновесии, то есть

,

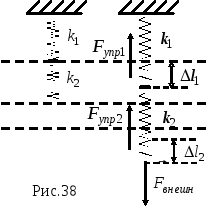
где и - упругие силы, действующие в пружинах 1 и 2 соответственно, - внешняя сила (рис.38). В начальном положении пружины не деформированы, поэтому энергия системы равна нулю

.

В конечном положении пружины растянуты, а энергия системы является энергией упругой деформации

,

где и - растяжение пружин 1 и 2 соответственно.

Воспользовавшись тем, что полное удлинение системы равно , а то есть откуда

и ,

и .

Тогда

,

.

5.6*. Потенциальная энергия частицы в некотором поле имеет вид , где a и b - положительные постоянные, r - расстояние от центра поля. Найти значение , соответствующее равновесному положению частицы. Выяснить, устойчиво ли это положение.

Решение. Частица находится в потенциальном поле. Потенциальная энергия частицы в этом поле - заданная функция одной координаты r. Проекция силы на направление радиус-вектора r может быть определена по формуле

В положении равновесия сила равна нулю:

,

откуда

.

Для построения графика найдем значение r , при которых потенциальная энергия равна нулю

,

.

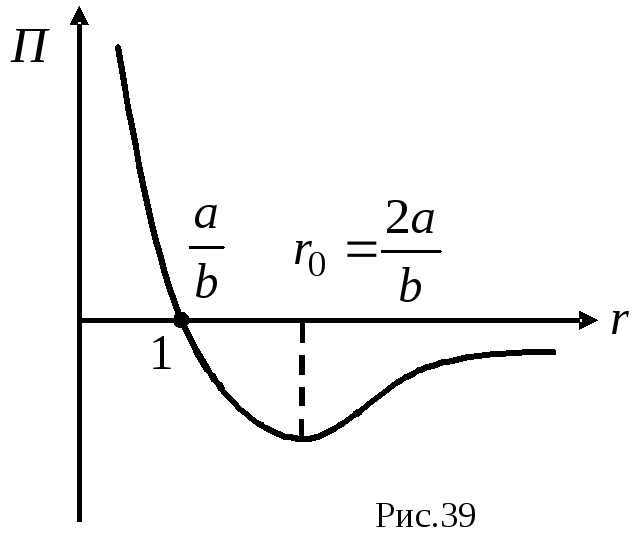
При потенциальная энергия . Качественный график зависимости потенциальной энергии от r представлен на рис. 39. Легко видеть, что при r, больше r₀. Следовательно, положение равновесия характеризуется минимумом потенциальной энергии. И соответствует положению устойчивого равновесия.