Модуль 2

Тема 4. Середні величини

ТЕОРЕТИЧНІ ОСНОВИ ТЕМИ

1. ПОНЯТТЯ ПРО СЕРЕДНІ ВЕЛИЧИНИ

Побудова варіаційного ряду розподілу дає можливість з'ясу­вати, як варіюють ознаки і як розподіляються одиниці сукуп­ності за цими ознаками (варіантами). На наступному етапі тре­ба знайти такі характеристики, які відображають властивості ряду розподілу в цілому, якомога повно характеризують дослід­жувану сукупність і притаманні їй закономірності. Тобто, треба знайти такі узагальнюючі характеристики, за допомогою яких можна було б порівнювати ряди розподілів різних статистичних сукупностей по відношенню до однієї й тієї ж ознаки; або до од­нієї й тієї ж сукупності, але по відношенню до різних ознак. Мова йде про визначення центрального числового значення оз­наки, яке відображувало б кількісно той типовий рівень, яким наділені елементи досліджуваної сукупності і навколо якого ма­ють тенденцію зосереджуватися спостережувані значення озна­ки. Математична статистика розглядає кілька різних таких по­казників центральної тенденції ознаки. Найголовнішим серед них і найбільш поширеним е середня арифметична величина.

При зоровому сприйнятті показників рядів розподілу і їх графіків переконуємося, що розмір варіант має деякі загальні закономірності, які проявляються в тому, що їх величини гру­пуються навколо центра розподілу. За даними статистичного ряду при віддаленні від центра розподілу вгору і вниз, а при графічному зображенні при віддаленні вправо і вліво частоти постійно спадають. Тенденція значень ознаки постійно групува­тися навколо центра розподілу частот, статистичною характе­ристикою якого є середня арифметична , називається цент­ральною тенденцією.

Таким чином, виникає необхідність розрахунку характерис­тик статистичних рядів розподілу.

Найважливішою характеристикою варіаційного ряду розпо­ділу є середня величина. Статистичні середні відображу­ють об'єктивну наявність певних умов, які проявляються в кож­ній одиниці досліджуваної сукупності: вони дають узагальнюю­чу кількісну характеристику статистичним сукупностям одно­типних явищ по варіаційній ознаці. Середні величини відобра­жують характерну, типову величину ознаки одиниць статис­тичної сукупності, яка утворюється в конкретних умовах місця і часу під впливом всієї сукупності факторів. Дія різноманітних факторів породжує варіацію осереднюваної ознаки. Середня є загальною мірою їх дій, рівнодіючою всіх цих факторів. Харак­теризуючи сукупність за осереднюваною ознакою, вона нале­жить до одиниці статистичної сукупності. Так, середня заро­бітна плата одного робітника в тваринницькій галузі господар­ства являє собою відношення фонду заробітної плати (за пев­ний період часу) до загальної (середньої за той же період) чи­сельності робітників у тваринництві. Ця середня характеризує рівень оплати праці даної сукупності робітників (зокрема тва­ринників у господарстві), але щодо одного робітника.

У середній величині взаємопогашаються індивідуальні різ­ниці одиниць сукупності, які зумовлюються дією випадкових об­ставин і в яких знаходить свій прояв загальне, закономірне, властиве даній сукупності явище. Тобто, вона узагальнює або являє собою весь діапазон даних і є результатом абстрагування відмінностей, що притаманні одиницям сукупності. У ній ніве­люються випадкові відхилення, властиві індивідуальним значен­ням ознаки, яка вивчається, а також відображуються загальні умови, що формують досліджувану сукупність.

Середнє і індивідуальні значення осереднюваної ознаки діа­лектично пов'язані між собою як загальне і окреме. Вона є най­важливішою категорією статистичної науки, і найважливішою формою узагальнюючих показників. Значна частина категорій економічної науки визначається за допомогою середніх вели­чин, адже останні виступають у ролі методу наукового пізнан­ня. У такому разі йдеться про “метод середніх величин”, який широко використовується в економічних дослідженнях.

Середні величини можуть бути одержані в результаті бага­торазових вимірювань однієї і тієї ж ознаки (величини), напри­клад, розрахунок висоти гумусового горизонту при багаторазо­вих вимірах. Середні одержують і при вимірюванні однорідних величин, наприклад, визначення середньої врожайності зерно­вих культур у господарствах якого-небудь адміністративного району.

Розрахунок середніх передбачає обов'язковість обліку умов виникнення кожної індивідуальної величини, інакше обчислен­ня можуть призвести до фіктивних середніх. Щоб середня вели­чина відображувала типове і загальне для всієї сукупності, ос­тання повинна бути якісно однорідною.

У практиці економічної роботи використовується досить широке коло показників, обчислених у вигляді середніх вели­чин: середня врожайність, середня заробітна плата, середній рі­вень продуктивності праці тощо. У кожному конкретному ви­падку середні величини мають певний соціально-економічний зміст, який зумовлюється природою об'єкта, що вивчається (на­приклад, по середньому рівню одержаної продукції на одного працюючого на молочнотоварній фермі можна судити про ефек­тивність використання живої праці в тваринництві; показник се­реднього рівня гектарів умовної оранки з розрахунку на один трактор характеризує ефективність використання тракторного парку і т. ін.).

Середні величини в статистиці служать інструментом вив­чення об'єктивних закономірностей соціально-економічних явищ, формою виразу їх дії. Їм належить чільне місце в плано­во-еко­номічних розрахунках і економічних дослідженнях. Се­редні по­казники використовують для виявлення невикористаних внут­рішньовиробничих резервів, обгрунтування шляхів і напрямів підвищення економічної ефективності виробництва, впровад­ження нових прогресивних технологій, нової техніки і т. ін. Так, порівнюючи середню продуктивність тваринництва і серед­ню собівартість виробництва продукції цієї галузі при різних технологіях виробництва, можна розрахувати порівняльну еко­номічну ефективність цих технологій, аргументуючи прийнят­ність тієї чи іншої.

Середні величини можуть використовуватися в економіч­них дослідженнях як вихідна база для вивчення закономірнос­тей і тенденцій у русі показників, що характеризують розвиток явищ у часі. Наприклад, зіставлення серед них показників про­дуктивності праці та її оплати за десятиріччя розкриває харак­тер розвитку явищ за цей проміжок часу, окремо продуктив­ності праці і окремо оплати праці. Зіставлення відносних показ­ників динаміки (коефіцієнтів зростання) зазначених двох явищ дає уяву про характер і особливість співвідношень зростання чи зниження продуктивності праці щодо її оплати за певні про­міжки часу.

По середніх показниках передових господарств можна мати уявлення про резерви зростання (чи зниження) ефективності виробництва і фактори, що зумовлюють це зростання (чи зни­ження).

Як уже було зазначено, метод групувань  один з основ­них методів статистики. Метод середніх у поєднанні з методом гру­пувань  це складова частина науково розробленої статис­тичної методології. Середні показники органічно допов­нюють метод статистичних групувань.

Середні величини використовують не тільки для виміру со­ціально-економічних процесів і явищ, а й для уточнення і ви­вчення їх змісту, характеру і напряму розвитку.

2. ВИДИ СЕРЕДНІХ ВЕЛИЧИН.

Статистика розрізняє два типи середніх величин: об'ємні і структурні. Математична статистика поділяє об'ємні середні ве­личини на види: 1) середня арифметична; 2) середня геомет­рична; 3) середня гармонійна та ін.

Названі вище види середніх величин можна одержати з фор­мул степеневої середньої. Для незгрупованих даних фор мула степеневої середньої має вигляд:

Якщо дані згруповані і мають відповідні частоти (п_і), се­редня степенева визначається за формулою середньої зваженої:

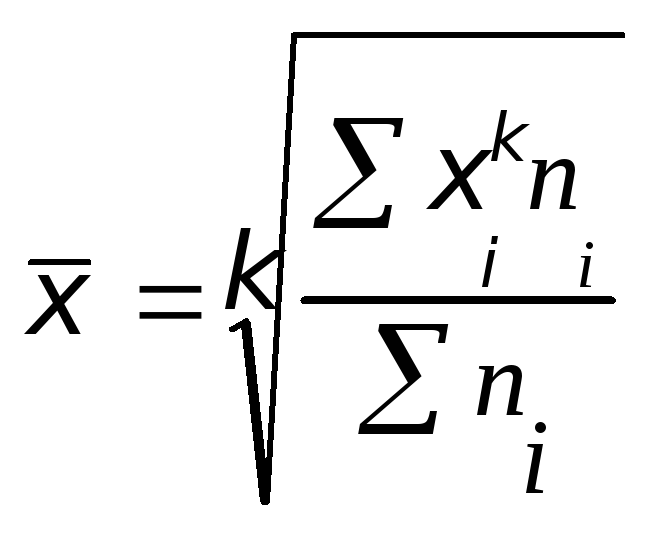
де  степенева середня; k  показник степеня, що виз­начає вид середньої; х  варіанта; п_i  частота (п = п_i).

Оскільки питання обгрунтування ваги при обчисленні се­редньої має важливе методологічне значення, розглянемо по­- няття ваги в статистиці взагалі і ваги середніх величин зокре­ма.

Під вагами в статистиці розуміють числа у вигляді абсо­лютних або відносних величин, які визначають значимість (ва­гомість) тієї чи іншої варіанти (ознаки) у даній статистичній су­купності.

Ваги середніх величин  це ваги, з якими окремі значен­ня усереднюваної ознаки беруться у розрахунок при обчисленні її

середньої величини. Вагами можуть бути показники чисельнос­ті одиниць або розміри статистичної сукупності у формі абсо­лютних чи відносних величин, і також величини показника, по­в'язаного з усереднюваною ознакою.

Середні, при розрахунках яких значення усереднюваної оз­наки (варіанти) зважуються по значеннях інших ознак, назива­ються зваженими середніми.

У наведеній вище формулі степеневої середньої зваженої за вагу прийнято частоту. У математиці і математичній статис­тиці, зокрема, де розрахунки абстрагуються від природи досліджува­них явищ, середню, розраховану за таким принципом, назива­ють середньою зваженою. Те­орія статистики дає обгрунтування обраної ваги для обчислення середньої.

Середня арифметична. Якщо в формулу степеневої се­редньої підставити значення k = l, то отримаємо середню ариф­метичну:

а) просту (незважену)

;

б) зважену

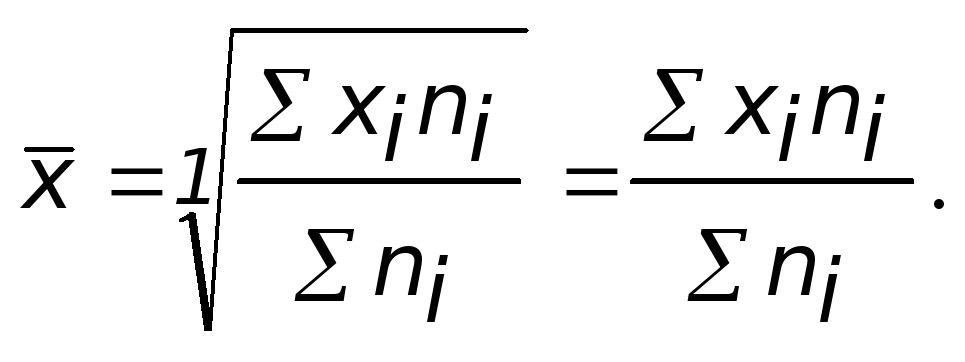
Так, якщо є х₁, х₂, х₃,..., х_n, то середня арифметична проста розраховується за формулою:

.

Як свідчить наведена формула, середню арифметичну просту одержують шляхом простого підсумовування всіх варі­ант усереднюваного показника і діленням одержаної суми на за­гальне число варіант.

Наприклад, якщо розміри ріллі по шести господарствах ста­новлять 2600 га, 3100, 4200, 3600, 4800 і 3900 га, тс середня її площа з розрахунку на одне господарство дорівнюватиме:

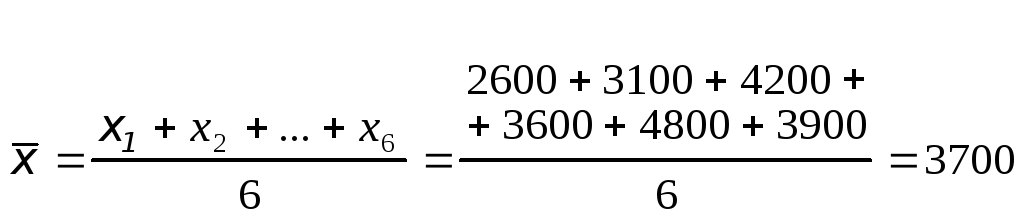(га).

Отже, якщо є первинні дані про величину ознаки у кожній окремій одиниці спостереження і треба обчислити середню ве­личину ознаки у розрахунку на цю ж одиницю, то використо­вують формулу простої середньої арифметичної.

У розгорнутому вигляді формула середньої арифметичної зваженої має вигляд:

.

Приклад. За даними про врожайність зернових культур на дослідних ділянках розрахувати середню арифметичну (табл. 4.1). Одержуємо:

(ц/га).

З наведеного прикладу бачимо, що середня арифметична зважена розраховується відношенням суми добутків усередню­ваних ознак на їх ваги до суми ваг. За вагу середньої зваженої беруть показники, які знаходяться у знаменнику вихідного від­ношення, тобто вихідної бази розрахунку середньої (логічної формули середньої). У розглядуваному прикладі вагами є показ­ники посівних площ, а їх сума (загальна площа) являє собою показник, який знаходиться в знаменнику, вихідної бази розра­хунку середньої урожайності. У конкретному випадку за вагу взято посівні площі ділянок, оскільки вони є доданками знамен­ника вихідної бази розрахунку середньої.

При обчисленні середньої арифметичної зваженої обрана вага повинна бути обгрунтована. Так, не можна ототожнювати частоти варіаційного ряду розподілу і ваги середньої арифме­тичної зваженої. Частоти можна використовувати як ваги лише при умові, що їх сума, тобто чисельність сукупності, яка підля­гає групуванню при побудові варіаційного ряду, являє собою знаменник вихідного відношення у розрахунку середньої. Таке зу­стрічається не завжди. Для нашого прикладу вихідна база роз­рахунку середньої урожайності виражається відношенням вало­вого збору зернових культур до площі посіву. Щоб знайти в цілому по сукупності валовий збір зернових культур, потрібно

Таблиця 4.1. Вихідні і розрахункові дані

Урожайність, ц/га (хі)	Площа Ділянки, га (пі)	хіпі
17,6	7	123,2
21,6	11	237,6
25,6	18	460,8
29,6	9	266,4
33,6	5	168,0
37,6	5	188,0
41,6	2	83,2
Всього	57	1527,2

по кожній групі ділянок помно­жити середню урожайність (х_i) на розмір по сівної площі в ге­ктарах (n_i) і скласти одержані добутки. Середню урожайність зернових по сукупності одер­жимо шляхом ділення знайде­ної суми добутків (x_іn_і) на за­гальний розмір посівної площі (n_і).

У цьому випадку за ваги при обчисленні середньої ариф-

ме­тичної взято доданки показника, який знаходиться у зна­менни­ку вихідної бази розрахунку середньої. Але цим доданком ви­ступає не частота варіаційного ряду  кількість ділянок (7), на яких одержано дану урожайність,  а посівні площі цих діля­нок. Використання даної ваги пояснюється тим, що при побу­дові варіаційного ряду групувались ділянки, середня ж урожай­ність визначається у розрахунку не на одну ділянку, а на 1 га посіву.

Математичні властивості середньої арифметичної. Середня арифметична як математична функція має ряд матема­тичних властивостей. Останні мають велике практичне значен­ня для розрахунку середньої за даними варіаційного ряду. Наз­вемо найважливіші з них.

1. Величина середньої арифметичної не змінюється, якщо частоти ряду розподілу замінити частостями:

,

де  відповідно частота і частість ряду розподілу.

Добуток середньої на суму частот завжди дорівнює сумі до­бутків варіант на частоти:

.

2. Якщо до варіант ряду розподілу додати або відняти од­ну й ту ж величину, то середня арифметична, обчисле­на з нових (змінених) варіант, збільшиться (або змен­шиться) на цю ж величину:

а) , звідси .

á) , звідси .

3. Якщо варіанти ряду помножити або поділити на одну й ту ж величину, то середня арифметична із змінених ва­ріант буде відповідно більшою або меншою в стільки ж разів:

а) звідки

б) звідки.

Середня гармонійна. Одержують її при підстановці у формулу степеневої середньої значення К = -1:

.

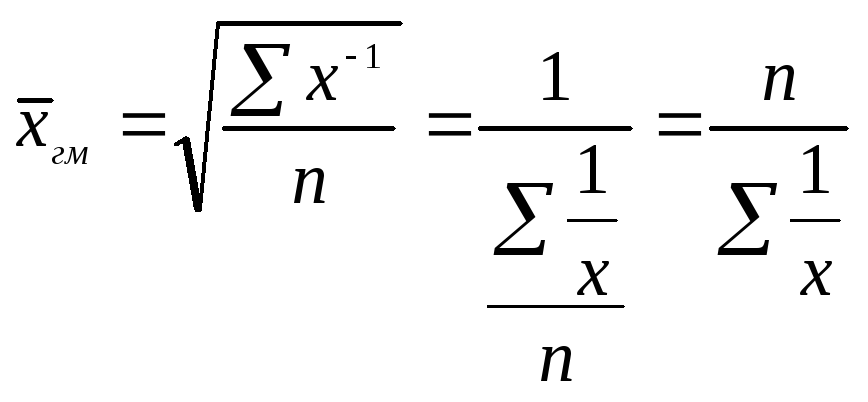Одержаний математичний вираз являє собою формулу се­редньої гармонійної простої, де  сума обернених значень варіант (ознак).

Ваги середньої арифметичної і середньої гармонійної знахо­дяться у відповідній залежності, а саме: , звідки . Підставляючи у формулу середньої арифметичної зваженої зна­чення , одержимо формулу середньої гармонійної зваже­ної:

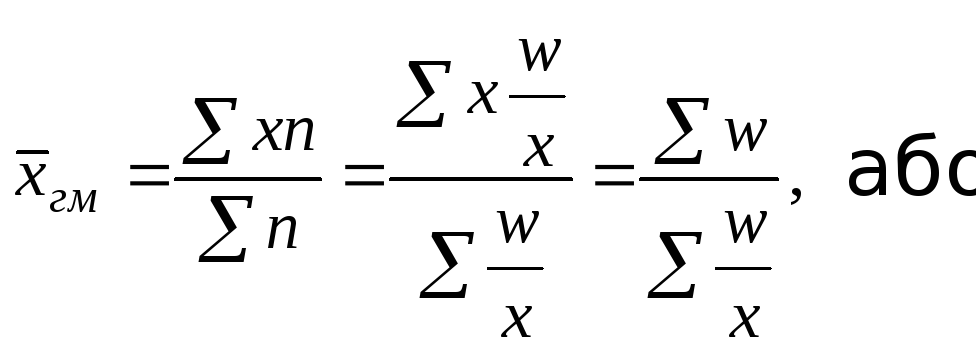
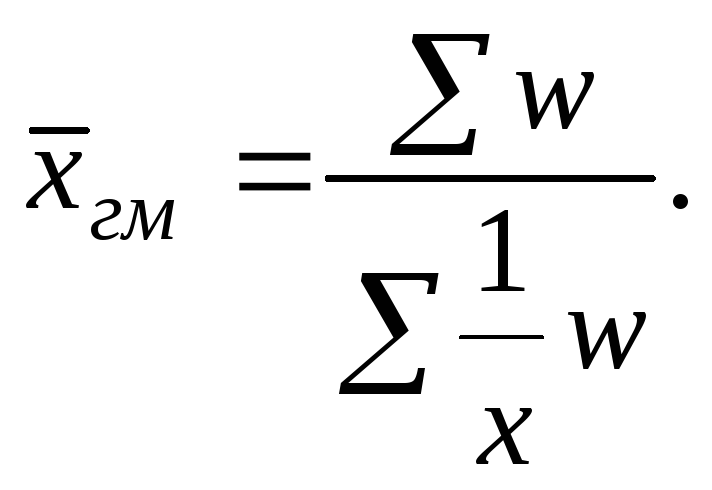
Як видно, середня гармонійна являє собою обернену ве­личину середньої арифметичної з обернених величин даних чи­сел.

Приклад. За даними врожайності і валового збору зерна, визначити середню гармонійну зважену (табл. 4.2):

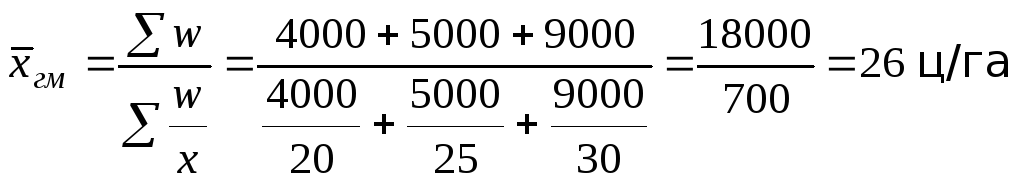
При розрахунку середньої гармонійної можна значно спро­стити обчислювальну роботу, якщо використати у розрахунках таблицю обернених чисел.

При розрахунку середньої гармонійної можна значно спростити обчислювальну роботу, якщо використати у розрахунку таблицю обернених чисел

Таблиця 4.2.Вихідні і розрахункові дані

Урожайність,ц/га (xi)	Валовий збір, ц (w)
20	4000	200
25	5000	200
30	9000	300

Всього

Таким чином, середня гармонійна знаходить застосування, коли безпосередні дані про ваги відсутні, а відомі варіанти усе­редненої ознаки х і добутки значень варіант на кількість оди­ниць, які наділені даним її значенням

Середня геометрична визначається за формулою:

Отже, середня геометрична являє собою корінь степеня чи­сла спостережень з добутку даних чисел:Після ло­гарифмування маємо:

Таблиця 4.3. Вихідні і розрахункові дані для обчислення середньої геометричної

Роки	Поголів'я корів, гол.	Коефіцієнт Зростання (К)	Логарифм числового значення коефіцієн­та зростання
2004 2005 2006 2007 1992 1993 Ñóìà 1993 Сума	623 670 728 800 883 906 	 1,07545 1,08657 1,09891 1,10375 1,02605 	 0,0315 0,0363 0,0411 0,0429 0,0111 0,1629

Значення х дорівнює антилогарифму .

Отже, середню геомет­ричну можна розглядати як антило­гарифм серед­ньої арифметичної з ло­гарифмів даних чисел. Цей вигляд середньої за­стосовують при розра­хунку середнього коефіцієнта зростання за певний період часу в рядах динаміки.

Приклад. За даними чисельності поголів'я корів за 6 років знайти середній щорічний коефіцієнт зростання поголів'я корів за період 2004-2007 рр. Проміжні розрахунки наведено в таб­лиці 4.3.

За даними таблиці знаходимо середнє значення з логариф­мів числових значень коефіцієнтів зростання:

.

Таким чином, розрахунок середнього коефіцієнта зро­стання поголів'я корів можна подати в такій послідовності:

.

До структурних середніх відносяться мода і медіана.

Таблиця 4.4. Вихідні і розрахункові дані для обчислення моди і медіани

Кількість приплоду, Гол. (хi)	Кількість Свиноматок, гол. (ni)	Нагромаджена сума частот (ni)
8	2	2
9	3	5
10	9	14
11	4	18
12	1	19
Сума	19	Х

Для дискретного ряду розподілу мода визначається за ча­стотами варіант і відповідає варіанті з найбільшою частотою.

Мода  це варіанта, яка найчастіше зустрічається у да­ному варіаційному ряду. Інколи її називають “модульна серед­ня”, або “домінанта”.

Медіана  це варіанта, яка припадає на середину варіацій­ного ряду. Якщо кількість членів ряду парна, то медіана дорів­нює середній арифметичній із двох серединних значень варіант.

Отже, на відміну від середньої арифметичної, яка розрахо­вується на базі всіх значень ознаки, мода і медіана характери­зують величину ознаки (варіанти), яка займає певне положення (місце) в ранжированному варіаційному ряду. Так, медіана зна­ходиться на середині ранжированного ряду. Місце медіани виз­начається її номером, зокрема: , де п  кількість одиниць спостереження. Визначимо значення медіани і моди по дискретному варіаційному ряду за даними таблиці 12.

Ранжирований ряд розподілу за кількістю одержаного при­плоду від однієї свиноматки має вигляд: 8, 8, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 12. Для визначення медіани маємо:

.

Отже, медіана дорівнює десятому значенню ознаки (ва­ріанти) в ранжированному ряду, тобто 10. По сумі нагромадже­них частот десятий член ряду має величину ознаки, що дорів­нює 10, тобто медіана дорівнює кількості приплоду 10 голів. Мода  величина, яка найчастіше зустрічається у досліджува­ній сукупності для даного ряду розподілу, також відповідає кількості приплоду 10 голів. Для інтервального ряду розподілу з рівними інтервалами інтервал, що містить моду (модальний), визначаº'гься за найбільшою частотою. При нерівних інтерва­лах мода знаходиться за показником найбільшої щільності роз­поділу.

Для випадку розподілу з рівними інтервалами мода (М_о) внутрішньомодального інтервалу обчислюється за формулою:

,

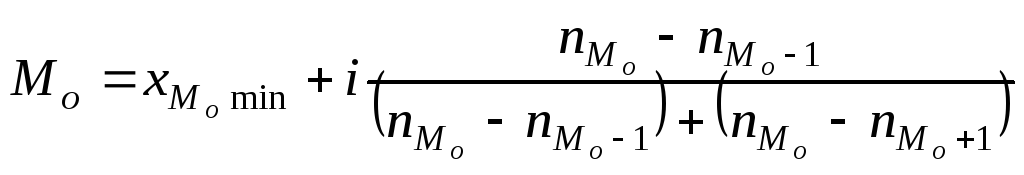де x_Mоmin  нижня границя модального інтервалу, і  вели­чина інтервалу, n_Mо  частота модального інтервалу; n_Mо-1  ча­стота інтервалу, що передує модальному; n_Mо+1  частота інтер­валу, що слідує за модальним.

Для обчислення медіани інтервального варіаційного ряду знаходять інтервал, який містить медіану, шляхом використан­ня нагромаджених частот або частостей. Медіанному інтервалу відповідає перша із нагромаджених частот або частостей, що перебільшує половину всього обсягу сукупності. Всередині знайденого інтервалу медіана (М_е) розраховується за форму­лою:

,

де x_Mеmin  нижня границя медіанного інтервалу; і  вели­чина інтервалу; 1/2n_і  половина суми всіх частот або частос­тей; S_Mе-1  нагромаджена частота чи частість інтервалу, який передує медіанному; n_Mе  частота медіанного інтервалу.

Карл Пірсон встановив взаємозв'язок між модою, медіаною і середньою арифметичною, який виражається рівністю:

.

Приклад. За даними інтервального ряду розподілу госпо­дарств по врожайності зернових культур знайти середній показ­ник врожайності, використовуючи у розрахунках формули стру­ктурних середніх  моди і медіани.

Таблиця 4.5. Вихідні і розрахункові дані для обчислення моди і медіани

Урожай­ність, ц/га (хi)	Кількість господарств, частота (ni)	Нагромад-жена сума частот, (ni)	Урожай-ність, ц/га (хi)	Кількість господарств, частота (ni)	Нагромад­жена сума частот (ni)
1620	3	3	3236	7	49
2024	6	9	3640	5	54
2428	17	26	4044	3	57
2832	16	42	Всього	57	

У складеному інтервальному варіаційному ряду за врожай­ністю зернових культур (табл. 4.5) модальним інтервалом із най­більшим числом варіант (17) є третій інтервал з рівнем урожай­ності від 24 до 28 ц/га. Отже, мода повинна знаходитися в се­редині цього інтервалу. Підставивши у наведену вище формулу необхідні значення, одержимо:

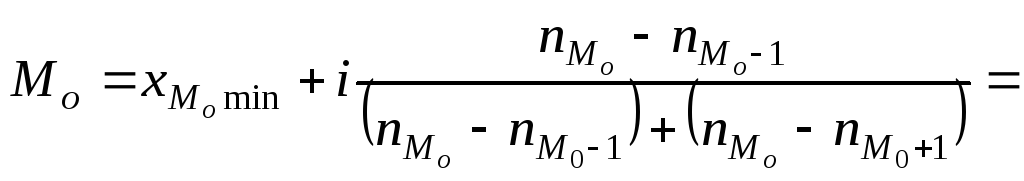
(ц /га).

Обчислимо медіану за даними цього ж інтервального ряду розподілу. Як уже було сказано, медіана (М_е) в статистичному ряду розподілу посідає центральне місце. Для її знаходження необхідно мати підсумок частот. Медіана знаходиться в тому ін­тервалі, нагромаджена сума частот якого дорівнює або більша за напівсуму частот ряду (57 : 2). У розглянутому прикладі та­ким інтервалом є четвертий, з рівнем урожайності від 28 до 32 ц/га, оскільки тут сума частот становить 42. Підставивши від­повідні значення в формулу медіани (М_е), одержимо:

ц/га.

Наведена формула розрахунку медіани дає наближене зна­чення середньої величини інтервального ряду розподілу, оскіль­ки вона грунтується на припущенні, що всередині медіанного інтервалу значення ознаки зростає строго рівномірно, що прак­тично зустрічається досить рідко (винятково). Враховуючи особли­вість зміни ознаки всередині медіанного інтервалу, як правило, наближену до рівномірної, розглядуваний прийом розрахунку медіани забезпечує вірогідність результатів розрахунку.

Невипадково моду і медіану називають структурними се­редніми. На відміну від об'ємних середніх, вони не пов'язані з підсумковою величиною ознаки, хоча і відображують конкретні характерні її значення. Так, начальний рівень середньої заробіт­ної плати працівника не пов'язаний певним кількісним відно­шенням з фондом заробітної плати. Знаючи моду і чисельність працівників, не можна розраховувати розмір фонду заробітної плати. Так само не можна розраховувати валовий збір зерна або валовий надій молока, якщо дані врожайності чи продук­тивності корів розраховані за модою або медіаною.

Отже, вказана методична особливість визначення таких ви­дів середньої обмежує в певній мірі їх практичне використання. Але як мода, так і медіана використовуються в статистиці для характеристики деяких типових розмірів соціально-економічних явищ у випадках, коли останні не можуть бути зображені за допомогою середніх величин. Так, при визначенні рівня ринко­вих цін на сільськогосподарську продукцію реєструють не се­редню ціну на ту чи іншу продукцію, а модальну, тобто ту, яка найчастіше зустрічається на обстежуваному ринку в період най­більш пожвавленої торгівлі. Зрозуміло, що точніший результат дав би розрахунок середньої зваженої ціни, але одержати точні дані для цього виду середньої (тобто кількість проданої продук­ції і її ціну) у зазначених умовах неможливо.

Безумовно, основною характеристикою центра розподілу є середня арифметична, адже базою її розрахунку є вся інформа­ція про досліджуване явище. Але інколи з практичних мірку­вань середню арифметичну замінюють модальним значенням або медіаною. Наведемо ще один приклад: при одержанні проб на якість продукції зручніше користуватися медіаною, адже для її визначення у ранжированному ряду не потрібно спеціальних розрахунків. У рядах розподілу з відкритими інтервалами також вважається доцільним використання моди і медіани. Моду ви­користовують при вивченні попиту населення на продукти хар­чування, одяг, взуття тощо. Практичний інтерес тут являє виз­начення модального розміру, тобто розміру явища, яке зустріча­ється найчастіше (у даному прикладі  найбільший попит).

3. МЕТОДОЛОГІЧНІ ПРИНЦИПИ ОБЧИСЛЕННЯ СЕРЕДНІХ ВЕЛИЧИН, УМОВИ ЇХ ТИПОВОСТІ

Середня вважається науково обгрунтованою, якщо методо­логічні принципи її обчислення відповідають певним ви­могам. Розглянемо найголовніші з них.

1. Розрахунок середніх величин повинен здійснюватися за однорідними, одноякісними явищами. Вимога однорід­ності усереднюваних ознак вважається найважливішою умовою типо­вості середніх. Тобто, останні можуть давати вірну характерис­тику статистичній сукупності лише у випадку, якщо одиниці, які входять у склад цієї сукупності, мало відрізняються одна від одної і якщо відсутня тенденція до концентрації значень ознак у чітко відокремлені групи. Отже, сукупність ознак повинна бути однорідною. А такою вона може бути у разі, якщо її частини підпадають під дію одних і тих самих причин. Середні, які за­стосовуються для характеристики однорідних сукупностей, яв­ляють собою наближену міру систематичного елемента статис­тичної сукупності, а відхилення значень окремих одиниць від середньої виникає під дією побічних причин. Якщо не врахову­вати умову, що середня є мірою систематичного елемента лише для однорідної сукупності, розрахунки матимуть суб'єктивний характер. Існує досить поширена помилка  визначення серед­ньої для неоднорідної сукупності, коли середня розглядається як міра дії основних причин, а відхилення від неї  як випад­кові. Це затушовує дійсну структуру статистичної сукупності і зумовлює неможливість викриття причин, котрі її викривляють (деформують). Середня, обчислена для різнорідних елементів, втрачає свій реальний зміст, перетворюється у фікцію.

Якщо досліджувана сукупність містить в собі відносно од­норідні частини і групи, у таких випадках доцільно обчислю­вати загальну середню і групові середні, адже названі види се­редніх відображують вплив різних умов. Так, загальна середня відображує загальні риси досліджуваного явища, а групові се­редні дають узагальнюючу характеристику рівню явища в більш конкретних умовах. Наприклад, середня собівартість виробниц­тва центнера яловичини в господарствах району (загальна се­редня) відображує загальний рівень вартості виробництва оди­ниці продукції в районі, а середня собівартість виробництва це­нтнера яловичини у фермерських господарствах (групова се­редня)  вартість виробництва даної продукції в умовах кон­кретної форми господарювання.

Отже, метод середніх повинен органічно поєднуватися з методом групувань. Таке поєднання має вирішальне значення статистичних і статистико-економічних дослідженнях. Загальні середні для однорідних суспільних явищ повинні доповнюватися середніми і індивідуальними величинами, які характеризують частини цілого (групи), прогресивне, відстаюче, окремі регіони тощо.

Аргументується ця умова тим, що оскільки в середній пога­шаються (вирівнюються) існуючі індивідуальні особливості, то за допомогою загальної середньої не можна виявити кращих до­сягнень чи відставань і т. ін. Тому в практичних чи наукових розрахунках не обмежуються загальними середніми, а доповню­ють їх груповими.

Таким чином, середні у статистиці лише тоді сприяють на­уковому аналізу, коли вони характеризують якісно однорідні су­купності. Якісна однорідність соціально-економічних явищ (а звідси і типовість середніх) встановлюється на підставі всебіч­ного теоретичного аналізу їх суті, розуміння економічного зміс­ту і знання природи цих явищ. Грунтуючись на теоретичних концепціях, статистика виділяє якісно однорідні сукупності за допомогою методу статистичних групувань.

Розглядаючи питання типовості середніх, зумовлених одно­рідністю статистичної сукупності, слід пам'ятати, що серед усе­реднюваних ознак можуть зустрічатися і досить відмінні одна від одної. Це цілком виправдано. адже в процесі розвитку явищ виникає нове і відмирає старе. Значення ознак представників нового і старого досить відмінні від середніх рівнів. Такі від­мінності цікавлять статистика не менше (а інколи і більше), ніж середні величини ознак, адже зрозуміло, що все нове, про­гресивне у суспільному житті знаходить підтримку, а виявлення старого, непрогресивного повинно спонукати на подолання його залишків досліджуваному явищі. Тому при поглибленому аналі­зі соціально-економічних явищ не обмежуються розрахунком лише середніх, а доповнюють їх описуванням окремих явищ, які мають значну варіацію щодо цієї середньої.

2. Наукова обгрунтованість середніх вимагає правиль­ного вибору явищ, тобто одиниць сукупності, за якими розрахову­ється середній розмір ознаки.

Пояснимо прояв даної вимоги при розгляді конкретних явищ.

Із логічної формули середньої випливає, що обчислюється вона як співвідношення двох показників, тобто як відношення обсягу ознаки до чисельності одиниць, які наділені цією озна­кою. Виходячи з цього принципу, обчислення середнього річно­го надою молока від однієї корови треба було б розрахувати від­ношенням валового надою за рік до чисельності поголів'я дій­них корів. У статистичній практиці дана середня величина роз­раховується щодо не дійних, а фуражних корів, а останні, як ві­домо, не всі дають продукцію. Такий спосіб розрахунку серед­ньої зумовлює стимул до зменшення чисельності недійних корів у господарствах. Аналогічного принципу дотримується статис­тика при обчисленні показника середньої урожайності. При йо­го обчисленні ділять валовий збір (урожай) не на збиральну чи фактично зібрану площу, а на весняну продуктивну площу. Ос­тання включає площі, на яких навесні може статися загибель посівів чи вони залишаться незібраними.

3. Середня величина повинна бути обчислена за всім ко­лом явищ, тобто спиратися на всі одиниці спостереження, інак­ше вона не буде дійсною характеристикою всього розподілу. У випадку, коли середня обчислюється не по всій сукупності, а лише по її частині, остання повинна репрезентувати сукупність, тобто бути представлена типовою її частиною. Вважається, що типовість середньої може бути забезпечена при чисельності оди­ниць спостереження не менше як 25-30. Надійну середню мож­на одержати і при меншій статистичній сукупності, але в та­кому разі досліджувані ознаки повинні відрізнятися одна від одної незначно. Тобто мінімальна кількість одиниць спостере­ження для одержання типової середньої у кожному випадку встановлюється, виходячи з конкретних умов. Але така кіль­кість одиниць повинна бути достатньою, щоб випадкові відмін­ності ознак не мали свого прояву і не сприяли формуванню су­б'єктивної середньої. Якщо коло явиш достатнє, питання про типовість середньої не виникає, адже в ній знаходять своє ві­дображення всі значення досліджуваних ознак.

Таким чином, середню слід розраховувати на базі достат­ньо великої кількості одиниць спостереження. Лише у такому випадку взаемовиключаються випадкові, індивідуальні відмінності між досліджуваними ознаками. Вони не справляють істотного впливу на середню. Якщо остання буде розрахована для неве­ликої чисельності одиниць сукупності, в ній знайдуть відобра­ження індивідуальні особливості ознак, тобто випадкові момен­ти, не характерні для сукупності в цілому. Така середня вва­жається нетиповою, ненадійною. Зі збільшенням обсягу сукуп­ності підвищується ймовірність одержання типової серед­ньої, зростає її пізнавальне значення. В основі такої залежності зна­ходить свій прояв дія закону великих чисел.

РОЗРАХУНКОВА РОБОТА

Завдання 1. За незгрупованими даними табл.4.6 обчислити середню арифметичну, моду та медіану.

Таблиця 4.6.Дані про кількість автомобілів по підприємствах

Номер підприємства	1	2	3	4	5	6
Кількість автомобілів,шт.	8	15	12	11	10	12

Виконання завдання 1.

С ередня арифметична проста обчислюється за формулою 4.1:

(4.1)

Мода це значення ознаки, яке найчастіше зустрічається в ряду чисел. В нашому прикладі це буде число 12 автомобілів (зустрічається 2 рази).

Для визначення медіани спочатку необхідно упорядкувати ряд чисел за зростанням (кількість автомобілів): 8, 10, 11, 12, 12, 15. Медіана знаходиться в центрі упорядкованого ряду чисел. В нашому прикладі центральну позицію займає пара чисел – 11 та 12. Отже, медіаною буде середнє значення з цих двох чисел, тобто 11,5.

Завдання 2. Обчислити середню арифметичну способом моментів на основі дискретного ряду розподілу господарств за кількістю працівників (див. результати виконання завдання 2 теми 3)

Таблиця 4.7. Розподіл господарств за кількістю працівників

Кількість працівників (Х)	Кількість господарств (n)
10	3
11	3
12	3
13	2
14	4
15	5
16	3
17	2
18	3
25	1
26	1
Разом	30

Виконання завдання 2.

Беремо в таблиці 4.7 число, наприклад, Х0 = 15 (близьке до середини упорядкованого ряду значень варіанти) за умовний нуль і число і = 2 за спільний дільник. Обчислюємо відхилення, які множимо на частоти (n – кількість господарств). результати обчислень наведені в табл. 4.8.

Таблиця 4.8. Обчислення середньої арифметичної способом моментів

Х-15	(Х-15)/2	(х-15)/2*n
-6	-3	-9
-5	-2,5	-7,5
-4	-2	-6
-3	-1,5	-3
-2	-1	-4
-1	-0,5	-2,5
0	0	0
1	0,5	1
2	1	3
9	4,5	4,5
10	5	5
Сума	Х	-18,5

Перший умовний момент складає Р = -18,5 :30 = -0,617, а середня арифметична = (-0,617) * 2 + 16 = 14,766 або округлено 15 (працівників).

Завдання 3. За згрупованими даними табл.4.9 обчислити середню арифметичну, моду та медіану.

Таблиця 4.9. Розподіл підприємств за рівнем

фондоозброєності праці

Група підприємств за фондоозброєністю праці,тис.грн. (X)	Кількість підприємств (f)
75-80	3
80-85	5
85-90	8
90-95	6
95-100	3
Разом	25

Виконання завдання 3.

Середню арифметичну для згрупованих даних обчислюють за зваженою фомулою (4.2):

(4.2)

Замінивши інтервали значень ознаки центрами інтервалів покажемо допоміжні обчислення в табл.4.10.

Таблиця 4.10. Розрахунки до обчислення середньої арифметичної зваженої

Х	f	Xf
77.5	3	232,5
82.5	5	412,5
87.5	8	700
92.5	6	555
97.5	3	292,5
Сума	25	2192,5

Використовуючи дані табл. 4.3, маємо:

Як видно з таблиці 4.9, мода знаходиться в інтервалі “85-90” (найбільша частота –8). Конкретне значення моди в інтервалі наближено обчислюють за формулою 4.3.

(4.3)

Отже, мода дорівнює: 85+5((8-5) : (16-5-6)) = 88 тис.грн.

Медіана належить підприємству, яке знаходиться в центрі ряду розподілу.Поділивши загальну кількість підприємств, знаходимо номер підприємства, яке знаходиться в центрі : 25 : 2 = 12,5, тобто номер 13.

Далі нагромаджуючи частоти ряду розподілу встановлюємо медіанний інтервал:

сума частот двох перших інтервалів складає : 3+5=8. Це менше ніж 13. сума частот трьох перших інтервалів складає : 3+5+8=16. Це більше числа 13. Таким чином, медіана знаходиться в третьому інтервалі “85-90”.

Медіану в інтервалі наближено обчислюють за формулою 4.4.

(4.4)

Отже, медіана дорівнює: 85+5((0,5*25-3-5) : 8)) = 87,8 тис.грн.

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

Завдання 1. За даними табл. 4.11 обчислити середню арифметичну (звичайним способом та способом моментів), моду і медіану для кожної з ознак ( Х та У).

Таблиця 3.11 Дані про урожайність зернових та внесення органічних добрив

Номер підприємства	Внесено органічних добрив на 1 га, т(Х)	Урожайність зернових культур, ц/га.(У)
1	18	25
2	22	20
3	25	30
4	15	20
5	19	28
6	16	22
7	20	31
8	20	20
9	17	20
10	14	25
11	0	30
12	18	20
13	19	25
14	19	29
15	17	22
16	26	29
17	14	27
18	25	20
19	21	28
20	15	26
21	15	24
22	22	25
23	22	21
24	25	20
25	17	20

Завдання 2. Обчислити середню арифметичну (звичайним способом та способом моментів), моду і медіану за даними табл.4.12.

Таблиця 4.12. Розподіл господарств за кількістю автомобілів

Кількість автомобілів (Х)	Кількість господарств (n)
8	4
9	4
10	4
13	3
14	4
15	6
16	4
17	2
18	3
20	1
22	1

Завдання 3. За даними табл.4.13 обчислити середню арифметичну (звичайним способом і способом моментів), моду та медіану.

Таблиця 4.13. Розподіл господарств за рівнем

урожайності картоплі

Група господарств за урожайністю картоплі, ц/га.	Кількість господарств
70-80	3
80-90	5
90-100	8
100-110	11
110-120	3
Разом	30