6. Координатна залежність електростатичного потенціалу в плоскому шарі та сферично симетричному об‘ємі

Розподіл самоузгодженого потенціалу в плоскому шарі рівноважної низькотемпературної плазми представляється найбільш простим.

У плоскому шарі плазми рівняння (7.11) спрощується і розподіл потенціалу описується вираженням:

. (8.1)

Рішенням цього рівняння є інтеграл:

, (8.2)

який можна привести до канонічного вигляду, визначивши межі інтегрування від значення до нескінченно великого значення потенціалу і здійснивши заміну :

, (8.3)

де є значення координати, при якому потенціал прямує до нескінченності. Тому граничні умови можна задавати відносно цієї координати.

Загальний вид рішень (8.3) представлений на рис. 5, з якого слідують три види розподілу потенціалу між плоскими пластинами щодо потенціалу плазми. Перше рішення не стосується прямої і прямує до нескінченності в точках і , причому граничні умови задаються в вигляді значень потенціалів та на обох пластинах. Друге асимптотично наближається до на нескінченності і тільки третє рішення, що відповідає різним знакам потенціалу відносно може перетинати вісь абсцис.

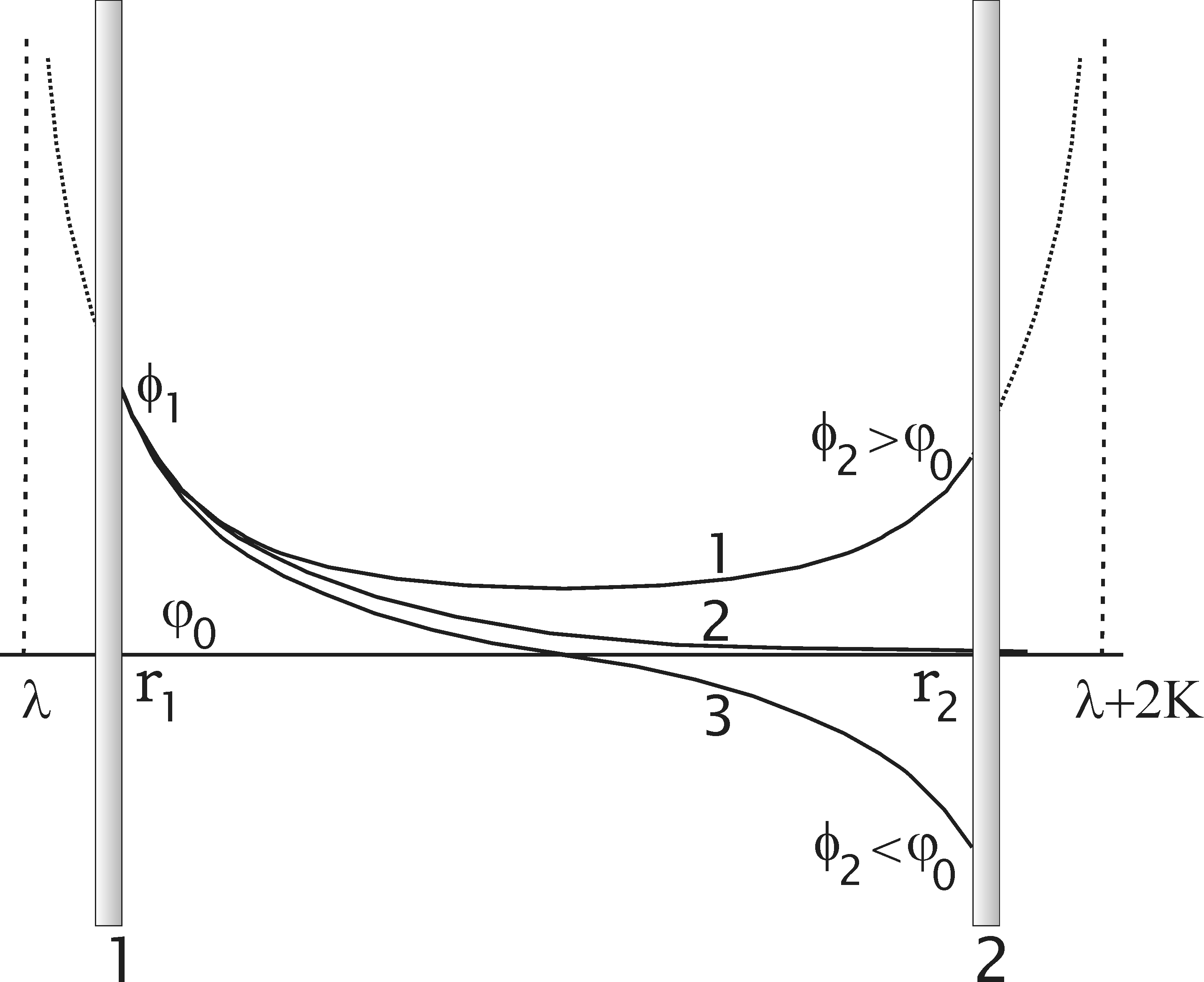
Рис.5. Розподіл потенціалу між двома плоскими пластинами в

плазмі.

1 – для випадку ;

2 – для випадку ;

3 - для випадку .

Звернемо увагу на те, що такі розподіли відносно нульового значення потенціалу отримані в роботах Дерягіна і Ландау Л.Д.. Але це не дозволило коректно визначити взаємодію між пластинами, тому що при вимірюванні потенціалу відносно Землі два різнойменних значення потенціалу можуть розташовуватися, наприклад, вище і мати зовсім інший вигляд розподілу.

Рішення рівняння (8.3) представляється в еліптичних функціях Якобі, а саме:

, ; (8.4a)

, , (8.4б)

де визначає знак потенціалу поверхні.

Ці вираження описують періодичні функції з періодом , де є повний еліптичний інтеграл I роду:

, (8.5)

для і для .

Це означає, що на відстані від точки функції (8.4а) і (8.4б) прямують до нескінченності, тобто для шару плазми товщиною повинні виконуватися співвідношення:

для

для .

Для забезпечення умов існування плазми необхідно, щоб розміри шару плазми були багато більше довжини екранування, чому відповідає . Великим значенням відповідають значення параметра . Наприклад, значенню (товщина шару плазми ) відповідає величина звідкіля випливає . Таким чином, вираження (8.4) має сенс використовувати тільки для опису розподілу потенціалу в шарі . В інших випадках досить рівняння

, , (8.6)

де

. (8.7)

Рівняння (8.6) після визначення константи еквівалентно рівнянню:

(8.8)

і може бути представлене в більш компактному вигляді:

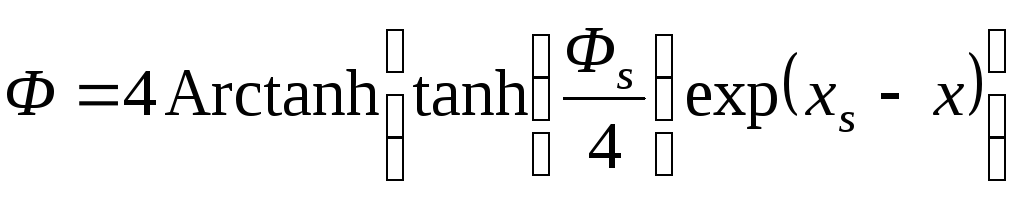. (8.9)

З рівняння (8.7) слідує, що потенціал змінюється від нескінченно великого значення до значення на довжині , до значення на довжині , до значення на довжині .

Отже, якщо відстань між площинами в плазмі більше 8D, то розподіл потенціалу відповідає випадку напівнескінченної плазми. Це означає, що електричне поле ні при яких обставинах не поширюється за межі чотирьох дебаївських радіусів від поверхні.

Для визначення значення повного потенціалу, яку можна назвати вимірюваним потенціалом, необхідне знання потенціалу плазми.

Значення потенціалу плазми біля поверхні електрода можна визначити через енергію поля в шарі просторового заряду, припустивши значення координати, що відповідає поверхні :

. (8.10)

Концентрації електронів і іонів задаються розподілом Больцмана:

, . (8.11)

Переведемо рішення рівняння Пуассона для напівнескінченної плазми (8.8) у розмірний вигляд і тоді одержимо:

,

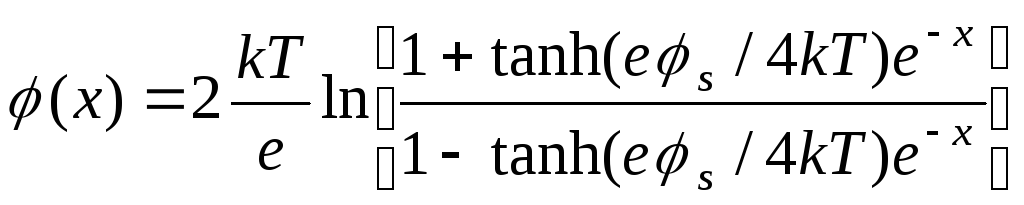. (8.12)

Перетворимо вираження (8.10) до вигляду:

. (8.13)

Вираження для похідної (8.12), з урахуванням рівняння (8.13) дає вираження для потенціалу плазми на поверхні плоского електрода:

. (8.14)

Тоді вимірюване значення потенціалу біля поверхні плоского електрода можна представити у вигляді:

. (8.15)

У випадку, якщо , це рівняння можна лінеаризувати:

. (8.16)

Наближення плоскої поверхні можна використовувати для великих часток у плазмі, коли радіус частки . З проведеного аналізу видно, що якщо відстань між частками більше 8D, то величиною в рівнянні (8.2) можна зневажити, і розподіл потенціалу відповідає випадку напівнескінченної плазми. Тобто електричне поле не поширюється за межі чотирьох дебаївських радіусів від поверхні частки. У реальній плазмі середня відстань між частками багато більше довжини екранування, тому взаємодія часток один з одним на далеких відстанях не може мати електричну природу.

Таким чином, опис розподілу потенціалу відносно дозволяє вибрати правильний вигляд залежності і коректно визначити взаємодію між зарядженими пластинами в плазмі.

Частки конденсованої дисперсної фази в плазмі продуктів згорання представлені в вигляді двох основних фракцій: мікронного і субмікронного розмірів; у деяких випадках субмікронна фракція також має два максимуми. В залежності від співвідношення між розміром часток і дебаївським радіусом екранування представляється можливість застосування плоского, чи сферичного рішення рівняння. Тому розглянемо розподіл електростатичного потенціалу в околиці дрібнодисперсних часток у плазмі в сферичних координатах.

Застосовуючи до рівняння (8.1) перетворення , , одержиме рівняння нової невідомої функції у вигляді:

. (8.17)

Так як

і ,

то щодо зворотної функції рівняння (8.17) запишеться так:

. (8.18)

Це рівняння є часткою більш загального диференціального рівняння іншого порядку:

, (8.19)

де і є дійсні числа, а є безперервна на деякій ділянці дійсної осі функція.

Для рівняння (8.19) отримані асимптотичні рішення при . Асимптотика при рішень рівняння (8.19) легко може бути отримана з зазначених результатів за допомогою деяких простих замін незалежної перемінної. Через цю обставину асимптотика поверхневого рішення рівняння може бути виписана в будь-якій точці з замикання області визначення цього рішення, що дозволяє описати глобальну картину поводження всіх рішень.

Для рівняння (8.18), можна побудувати якісну картину поводження всіх рішень, представлену на рис.6 і рис.7. Звідси видно, що при незмінному значенні потенціалу на поверхні частки, напруженість поля на поверхні зменшується із збільшенням радіуса частки. Тобто дрібні частки екрануються на більш коротких дистанціях.

Отже, максимальна дистанція поширення електричного поля є граничною для часток, тому що зі збільшенням кривизни поверхні ця дистанція зменшується.

Для рішень рівняння (8.18) щодо першої похідної можна виписати наступні асимптотичні співвідношення:

, (8.20a)

, (8.20b)

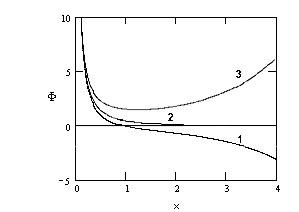
Рис. 6. Розподіл потенціалу в околиці частки радіусом .

1 – для випадку ;

2 – для випадку ;

3 – для випадку .

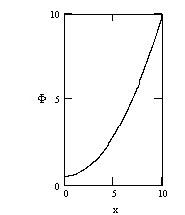
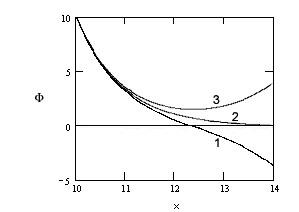
Рис. 7. Розподіл потенціалу в околиці частки радіусом (позначення кривих 1,2,3 аналогічно рис.6).

, , (8.20c)

, , (8.20d)

де - значення потенціалу в точці , - довільна крапка області визначення рішення. Постійна визначає вигляд залежності : якщо , то залежність має вигляд (1); якщо , то залежність має вигляд (2); якщо , то залежність має вигляд (3) рис.6 - 7.

Порівняємо вираження (8.20a) з вираженням для напруженості поля біля плоскої поверхні в плазмі:

. (8.21)

Легко помітити, що при потенціалі поверхні ( ), рівняння (8.21) збігається з рівнянням (8.20a). Звідси випливає висновок, дуже важливий для спрощеного опису розподілу потенціалу навколо заряджених часток, а саме: при великих значеннях потенціалу поверхні кривизну частки можна не враховувати, а використовувати рішення плоскої задачі (8.8):

, .

Таким чином, ми розширюємо застосування рівняння (8.8), що раніше використовувалося тільки для очевидного випадку .

Рівняння (8.20b) описує розподіл полючи в обмеженому об’єму плазми при відсутності усередині об’єму заряджених тел.

Рівняння (8.20c) після інтегрування збігається з потенціалом Дебая:

.

Рівняння (8.20d) справедливо в околиці будь-якої крапки , що належить інтервалу , де є радіус розглянутого об’єму плазми з часткою радіуса в центрі. Це рівняння може бути приведене до вигляду:

, (8.22)

де деяка функція:

(8.23)

залежить від перемінної і визначена в інтервалі .

У лівій частині рівняння (8.22) містить інтеграл, що є рішенням «плоскої задачі», тобто рішенням рівняння , що описує потенціал у плазмі в плоскої поверхні.

На підставі аналізу самоузгодженого рівняння Пуассона в сферичних координатах можна зробити наступні основні висновки:

(а) кривизна часток приводить до більш швидкої зміни потенціалу в їхній околиці в порівнянні з плоским випадком, тобто частки малого радіуса сильніше екрануються;

(б) при великих значеннях потенціалу поверхні кривизну частки можна не враховувати, а використовувати рішення плоскої задачі;

(в) на відстані від поверхні частки поле практично відсутнє, тому що значення потенціалу знижується від нескінченно великого значення до значення . Це означає, що в рівноважній пиловій плазмі, де відстань між частками , не може здійснюватися електростатична взаємодія між ними. Отже, джерела сил, відповідальних за упорядковування часток у плазмі мають не електричну природу.