Определение. Точка области определения функции называется стационарной, если в этой точке существуют частные производные первого порядка, и выполняется необходимое условие экстремума:

.

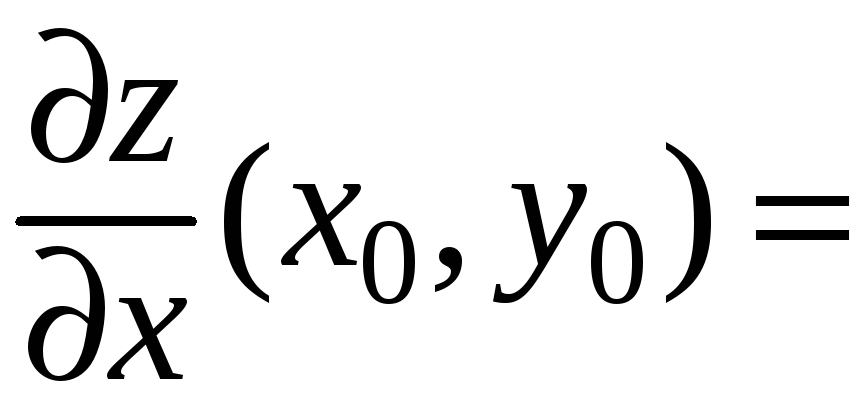
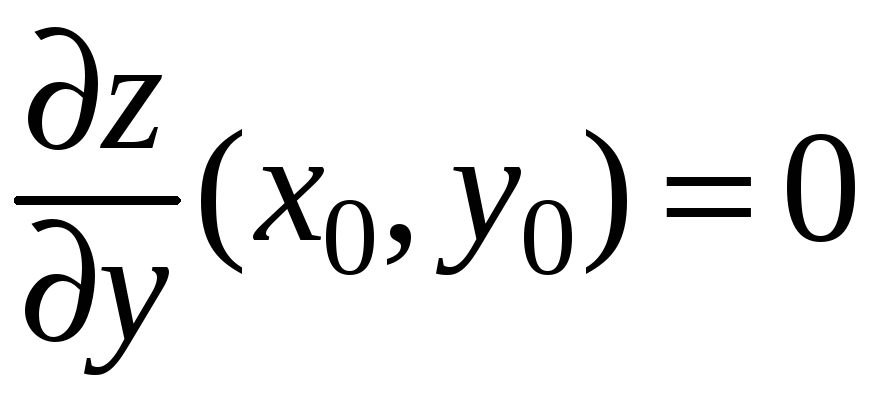Достаточное условие экстремума

Теорема. Пусть в окрестности стационарной точки функция имеет частные производные до третьего порядка включительно. Обозначим:

; ; ; .

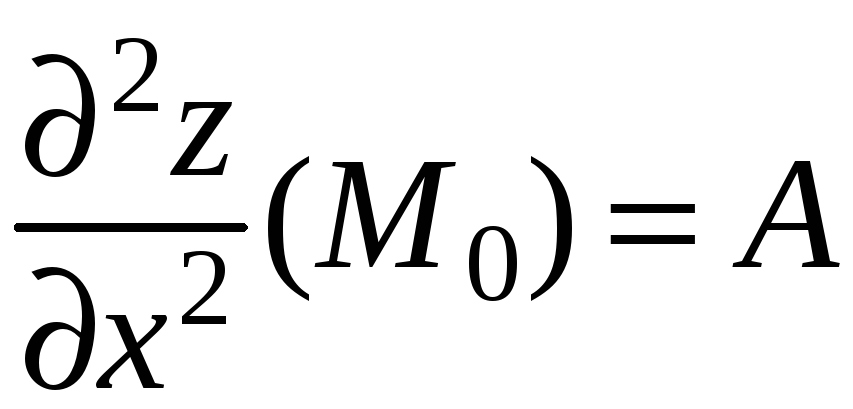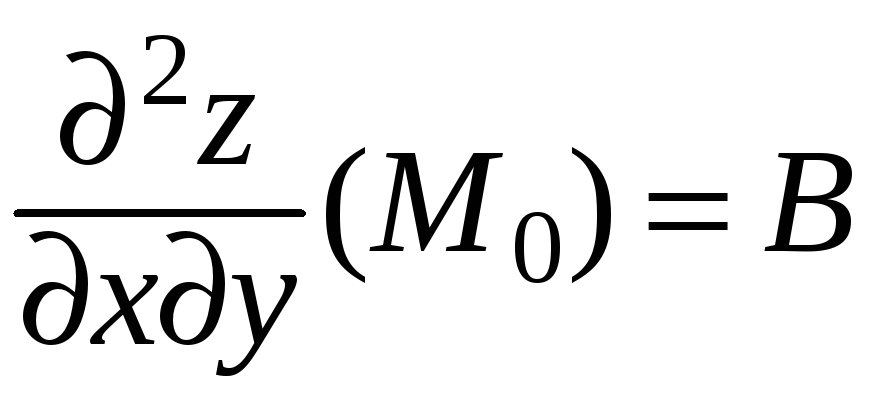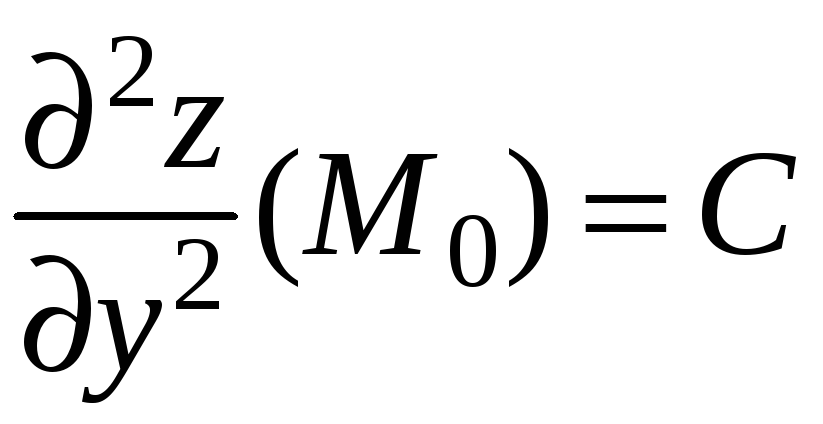Тогда:

1. Если 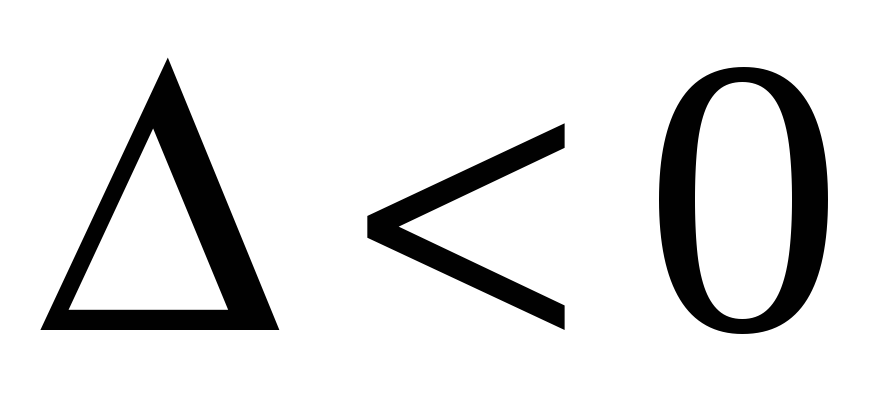, то в точке 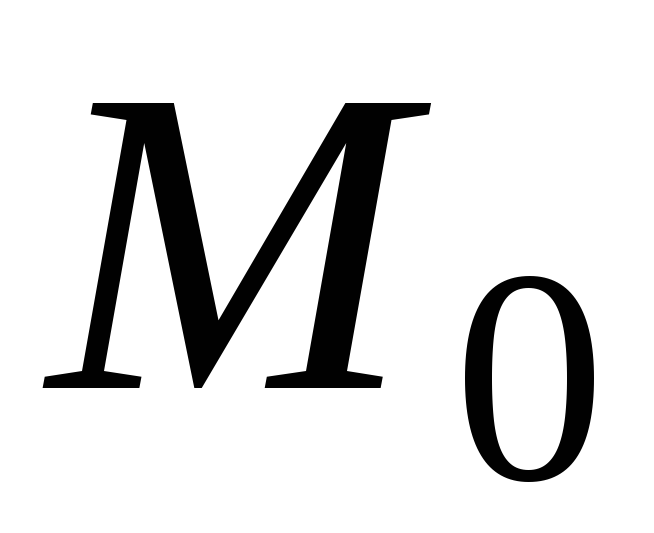экстремума нет.

2. , то в точке имеется экстремум; при этом:

если , то — точка максимума;

если , то — точка минимума.

(без доказательства).

Замечание. Если , то для решения вопроса о наличии экстремума требуется привлечение производных более высоких порядков.

Пример. Рассмотрим функцию

.

Здесь

; .

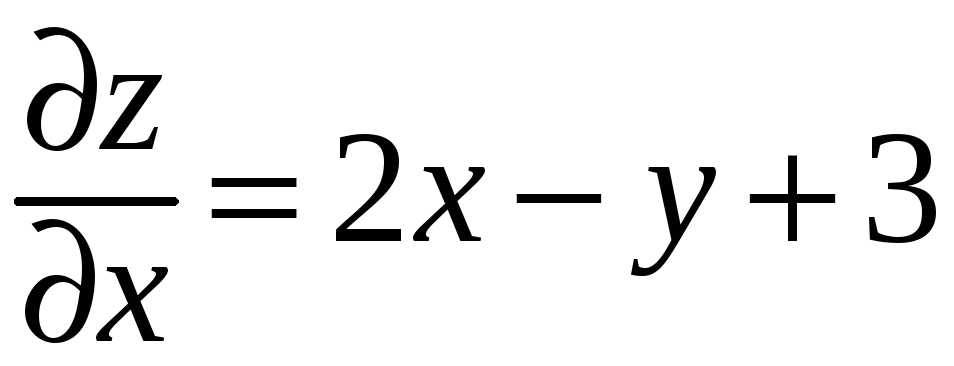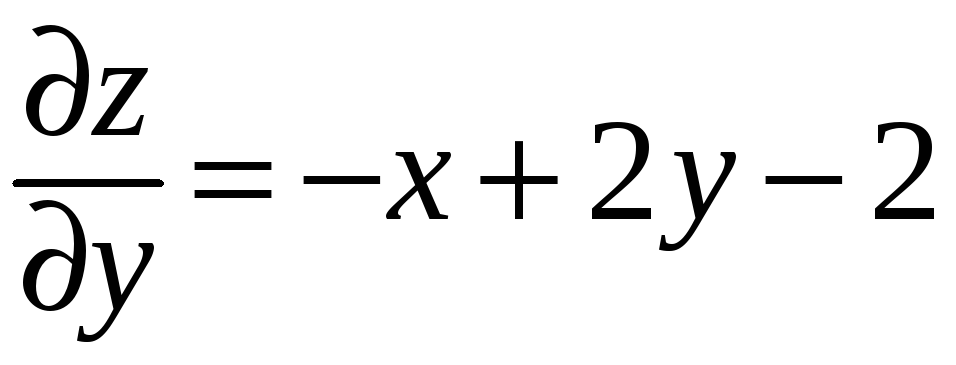Решая систему уравнений, находим стационарные точки путем решения системы уравнений:

.

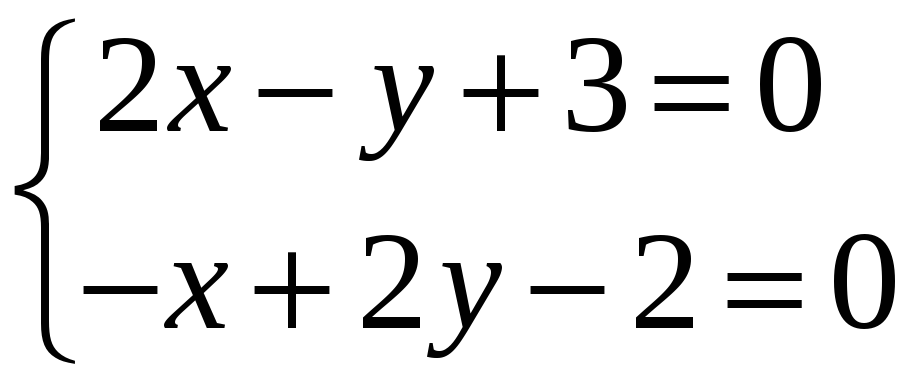Функция имеет единственную стационарную точку 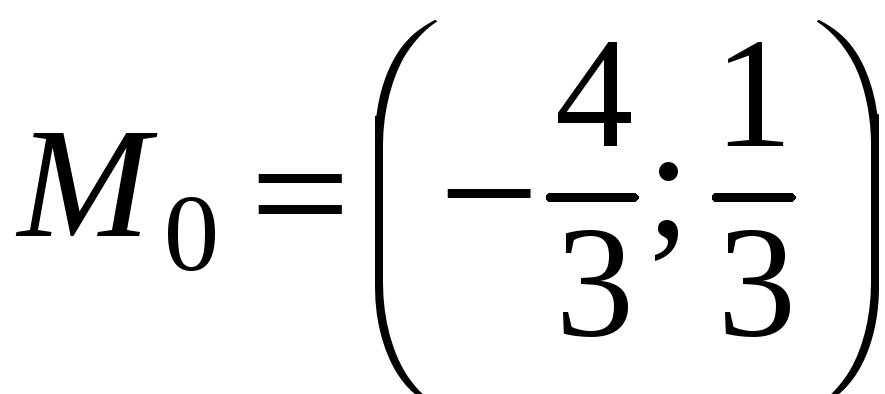. Находим частные производные второго порядка:

; ; .

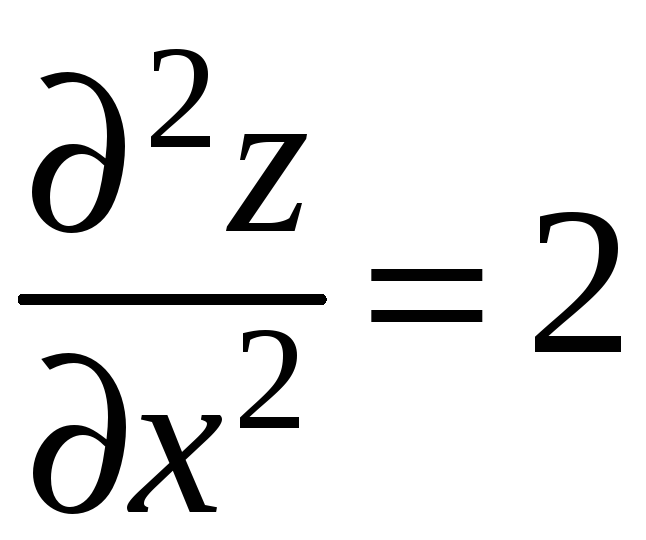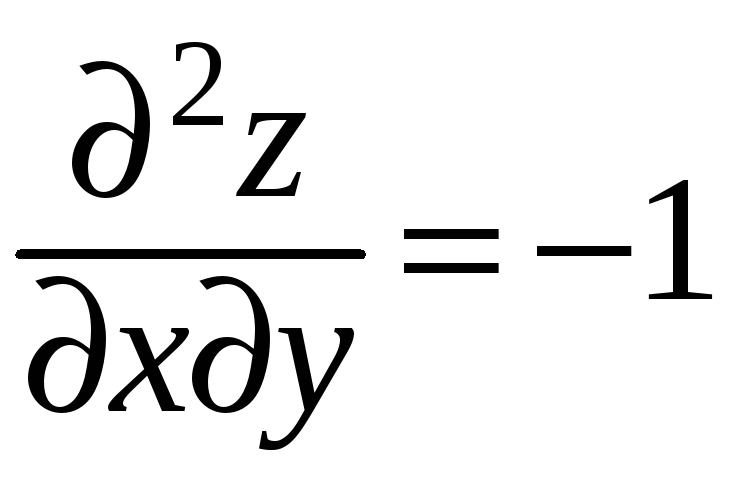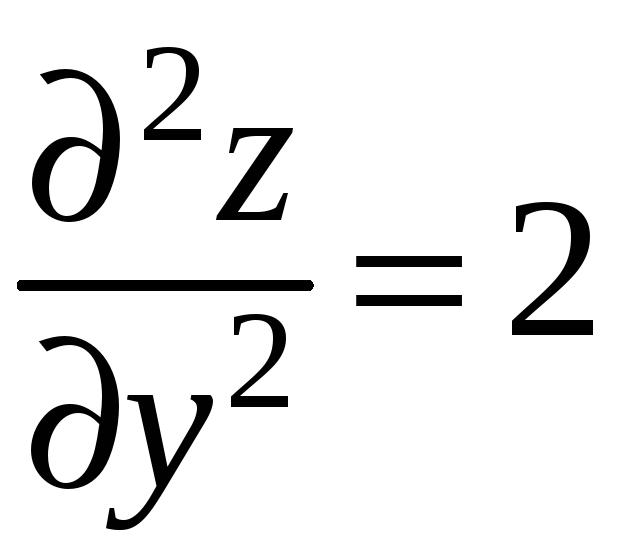Далее, , и . Значит, 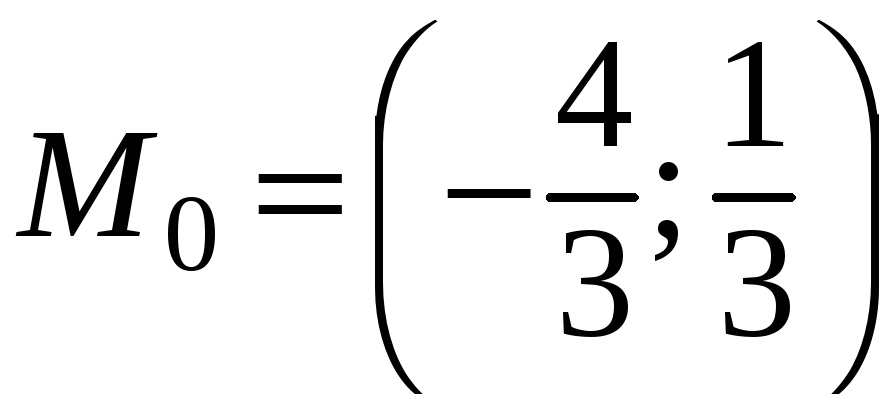— точка минимума.

14. Производная по направлению и градиент

I. Направляющие косинусы вектора

Н

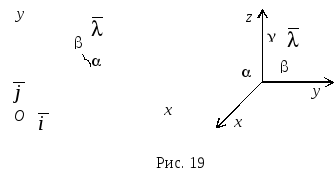
апомним, что для ненулевого вектора плоскости или пространства его направляющими косинусами называются косинусы углов, которые этот вектор образует с осями декартовой системы координат (рис. 19).

Если ненулевой вектор плоскости имеет в ортонормированном базисе, связанном с этой системой, координаты , то есть , то

; .

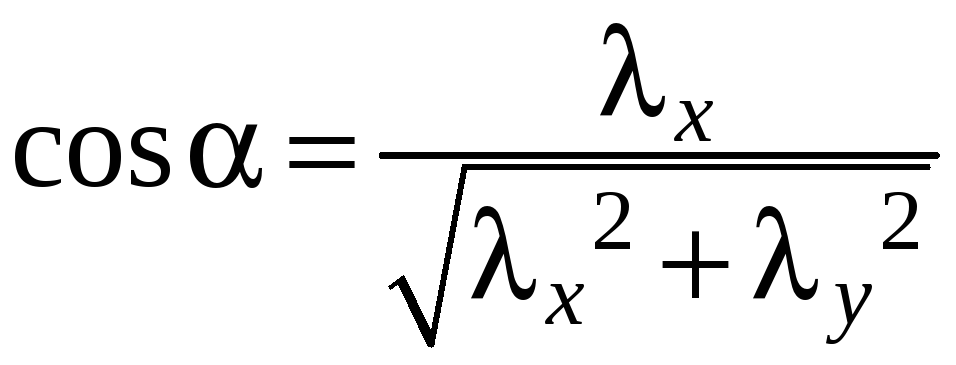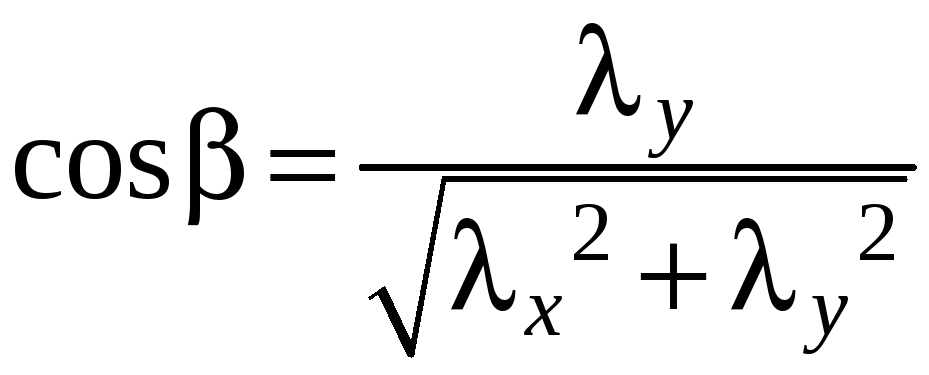Аналогично в случае ненулевого вектора пространства формулы для направляющих косинусов имеют вид:

; ;

.

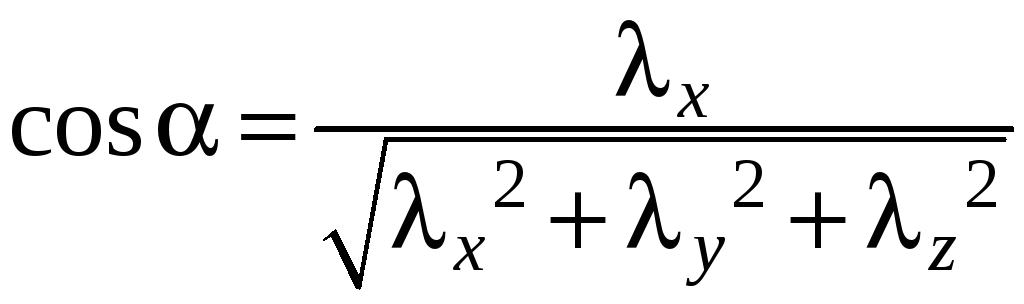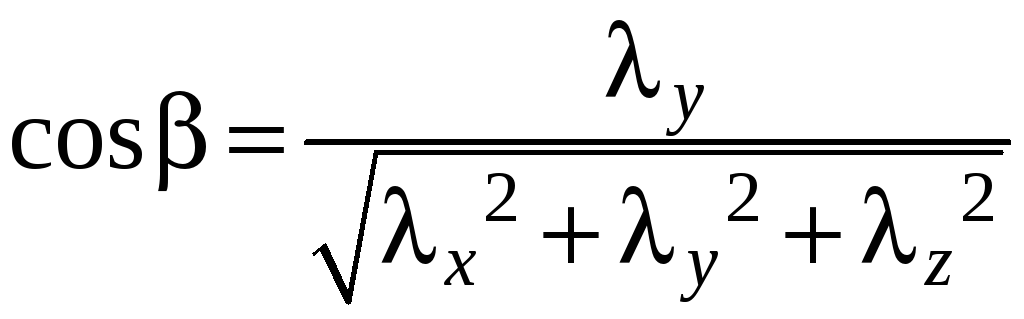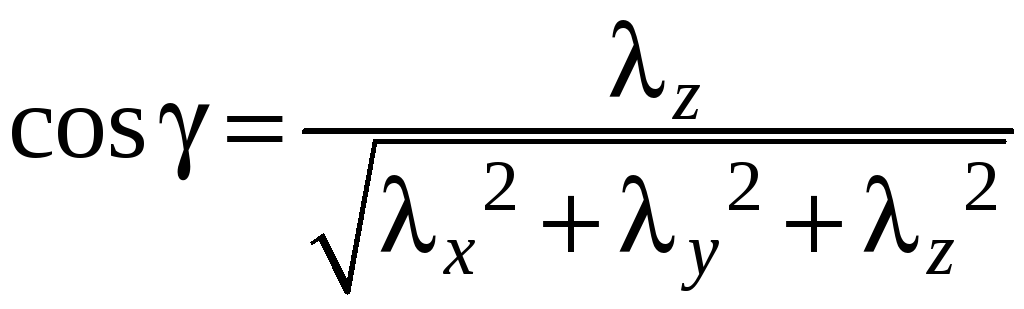Направляющие косинусы вектора задают его направление в пространстве. Вектор , координатами которого являются направляющие косинусы вектора, сонаправлен с вектором и имеет модуль, равный единице (рис. 20).

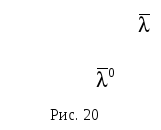
II. Понятие производной по направлению

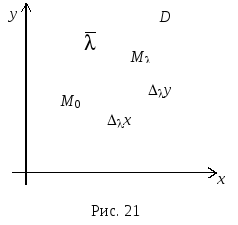
Пусть в области плоскости заданы функция двух переменных , точка , и ненулевой вектор . Будем выбирать переменную точку таким образом, чтобы вектор был сонаправлен с вектором (рис. 21).

Обозначим приращения независимых переменных при переходе от точки к точке через , ; соответств

ующее приращение функции через . Тогда

.

Определение. Пусть стремится к точке таким образом, что вектор остается направленным одинаково с вектором . Если существует конечный предел отношения 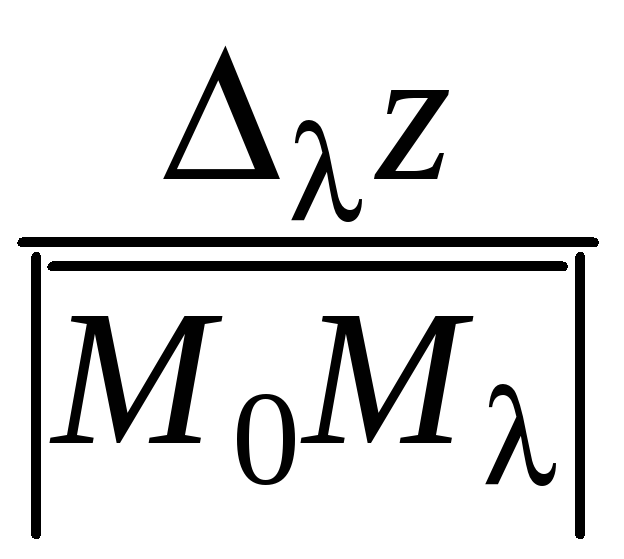при , то этот предел называется производной функции по направлению вектора в точке  .

Обозначение производной по направлению: 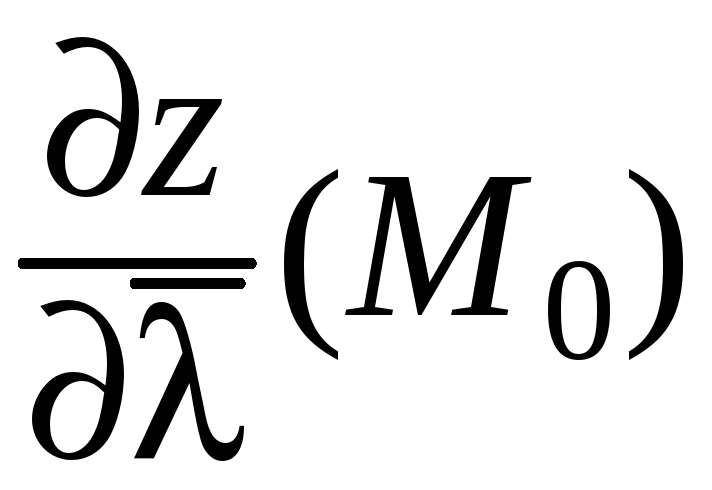. Итак, согласно определению:

.

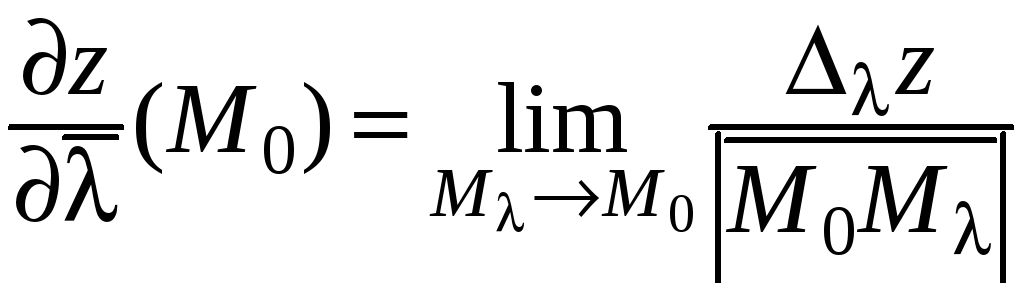Замечание. Производная по направлению показывает скорость изменения функции в точке в направлении вектора . В частности производные по направлению базисных ортов равны соответствующим частным производным:

.

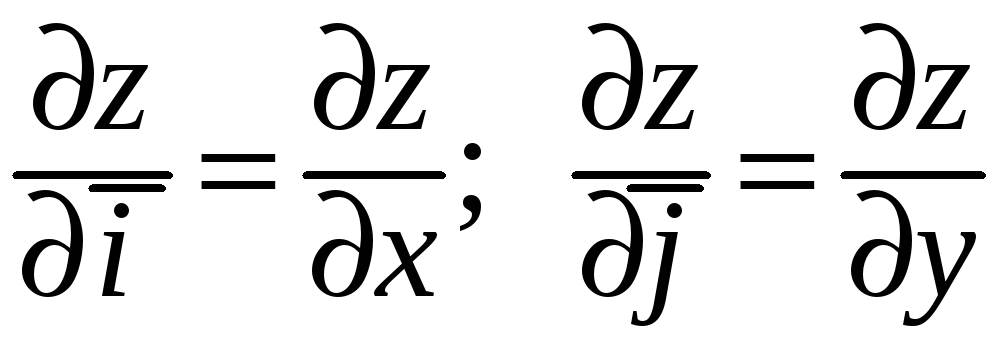Пусть вектор имеет направляющие косинусы , .

Теорема. Пусть функция удовлетворяет двум условиям:

1. В окрестности точки она имеет частные производные .

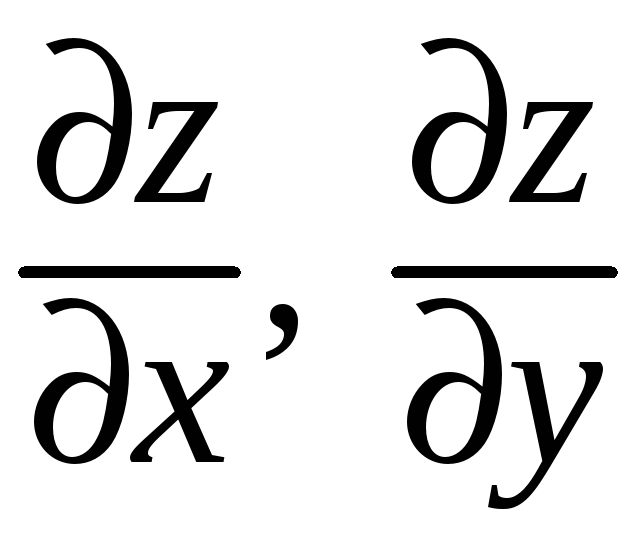2. В самой точке частные производные непрерывны.

Тогда для производной по направлению 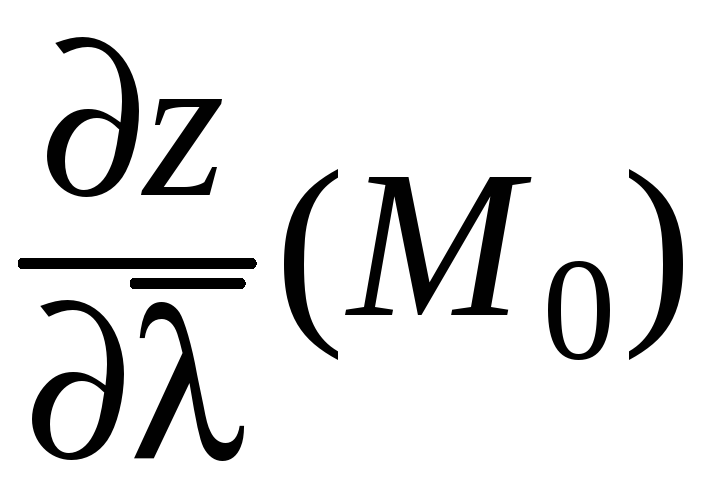справедлива формула:

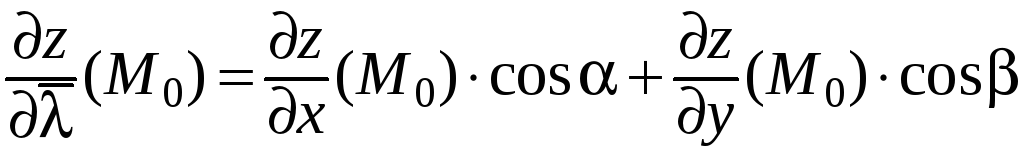. (24)

Доказательство. Пусть , — приращения независимых переменных, соответствующие переходу от точки к точке . Ввиду непрерывности частных производных для соответствующего приращения функции справедлива формула:

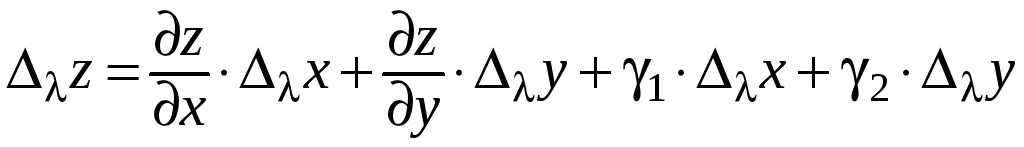, (25)

где функции и ― бесконечные малые величины при и (п. 6). Деля обе части (25) на , получаем:

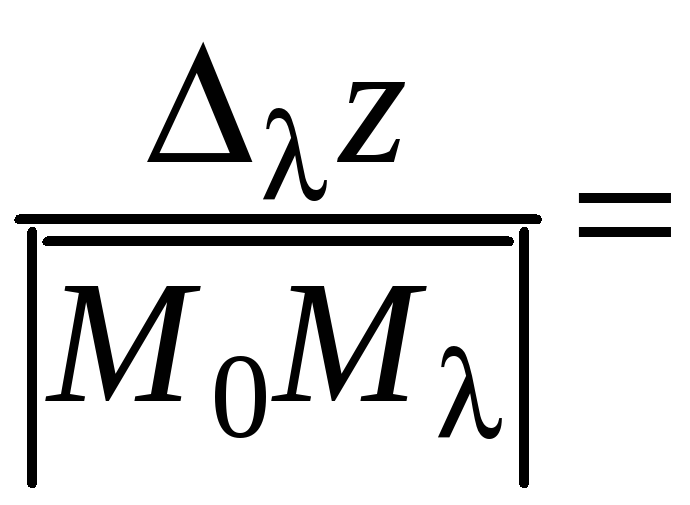
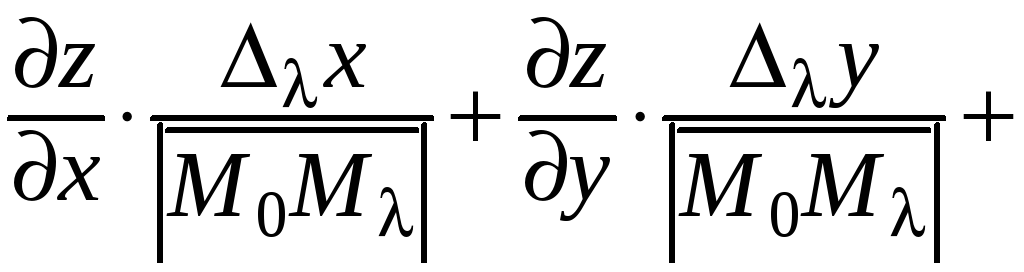
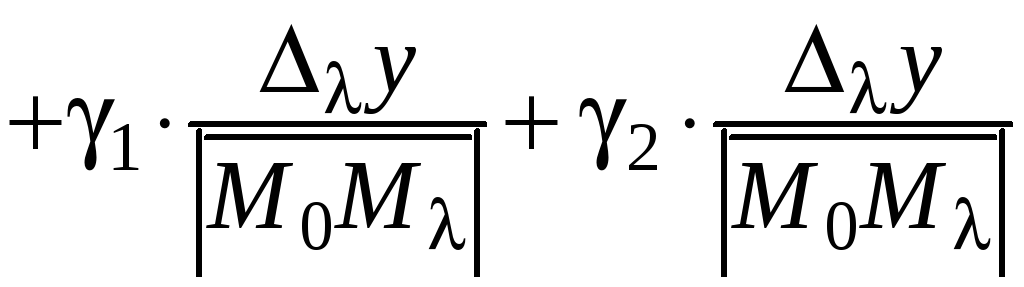. (26)

Поскольку вектор сонаправлен с вектором , то величина 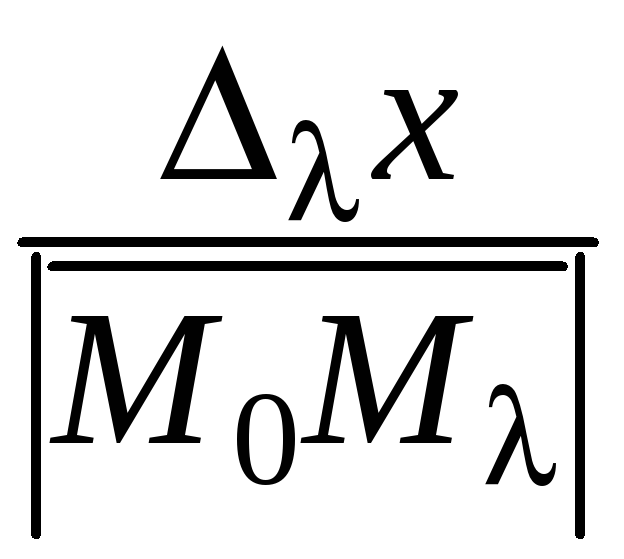, будучи направляющим косинусом вектора , совпадает с направляющим косинусом вектора : 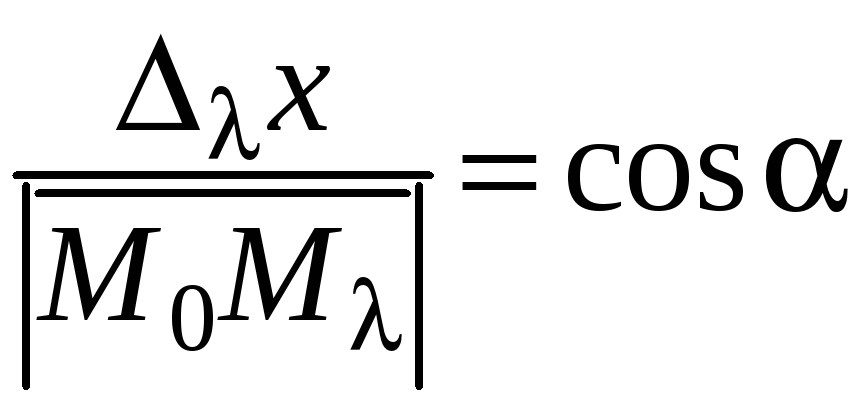. Аналогично .

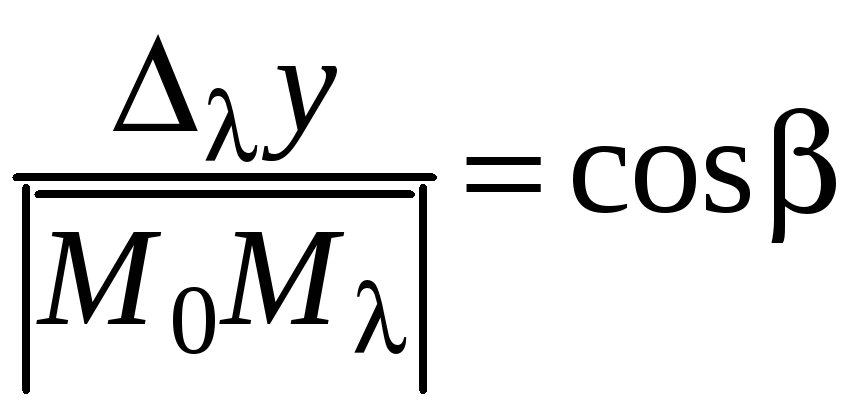Равенство (26) теперь принимает вид:

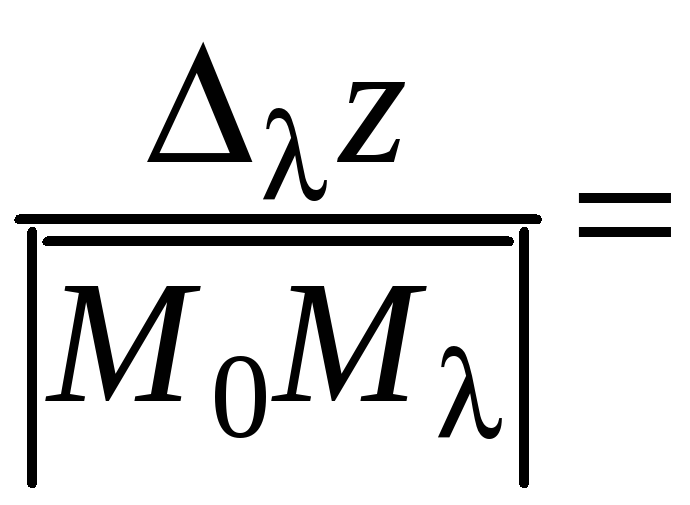
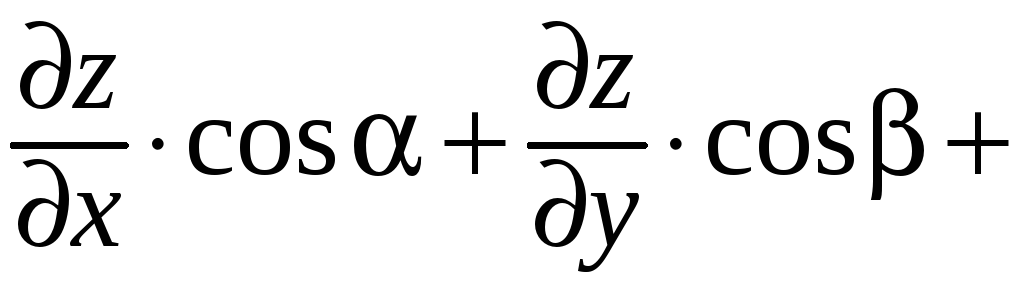
. (27)

Поскольку , , когда , то переходя в (27) к пределу при , получаем на основании свойств предела:

. ▄

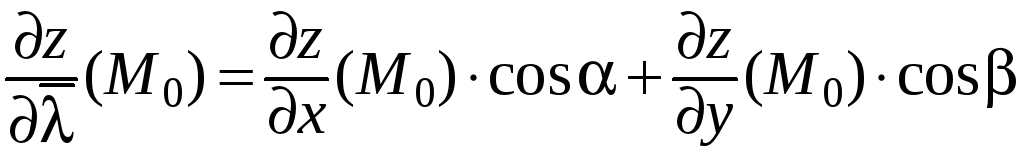Пример. Пусть , , . Вычислим производную по направлению 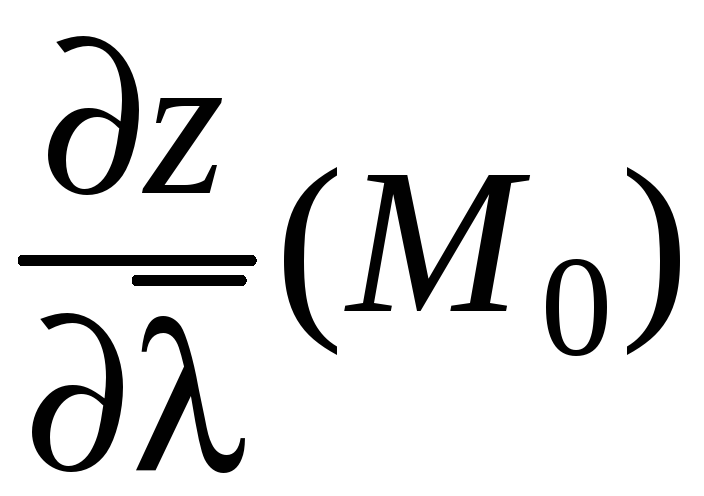. Находим частные производные:

; ;

; .

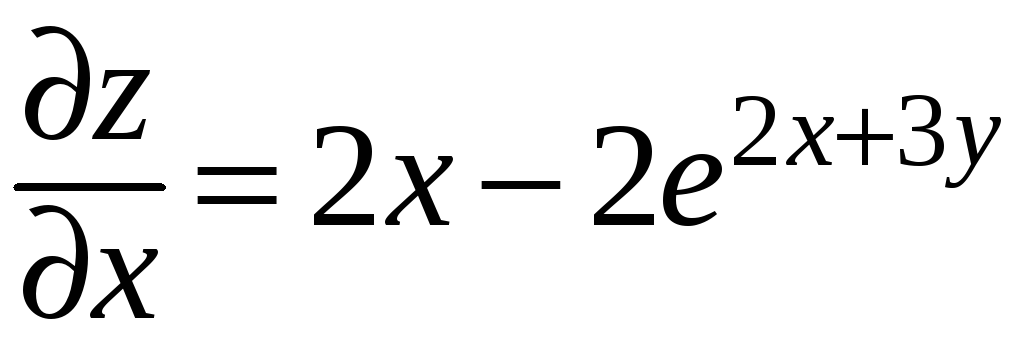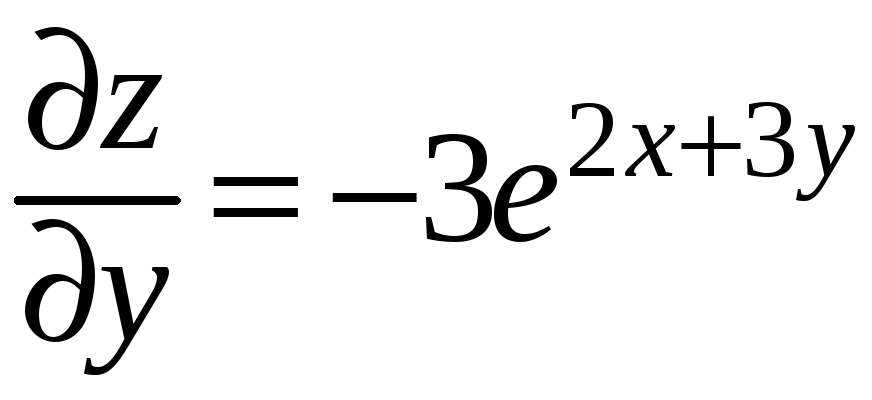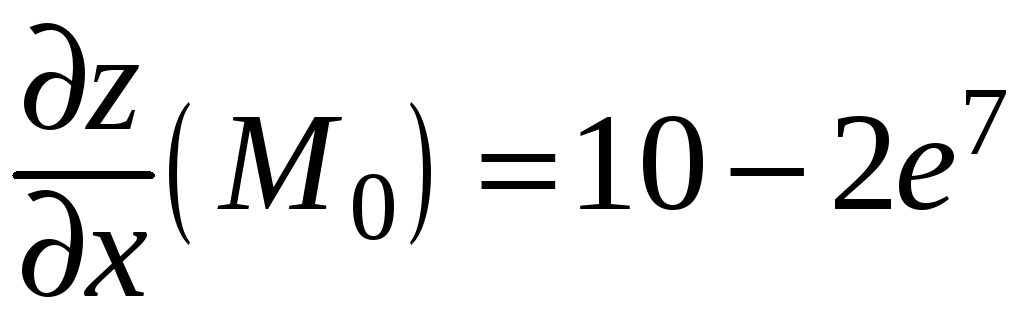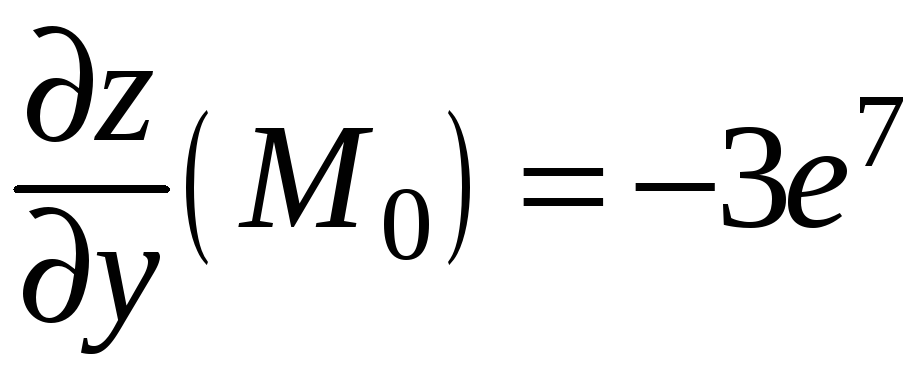Находим направляющие косинусы вектора :

; .

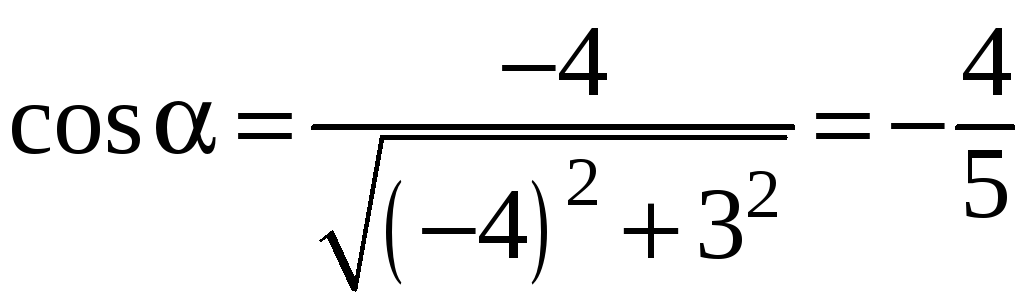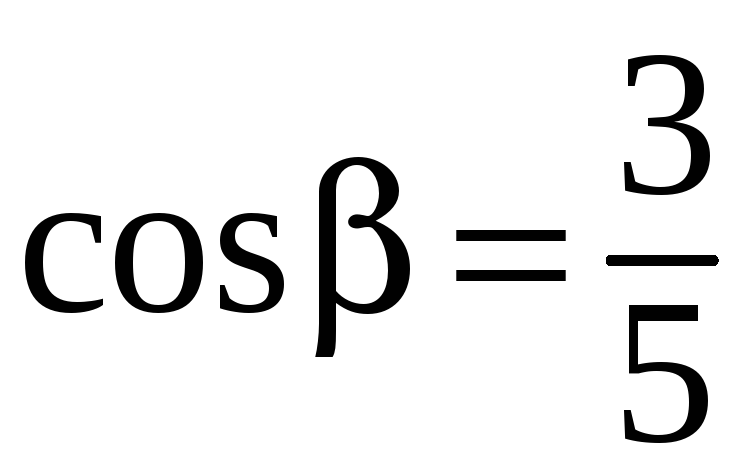Подставляем найденные значения в формулу (24):

.

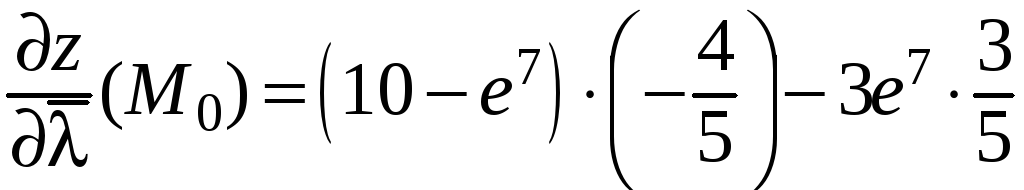Аналогичным образом определяется производная по направлению в случае функции трех или более переменных. Для функции трех переменных формула (24) (в случае непрерывности частных производных) принимает вид:

.
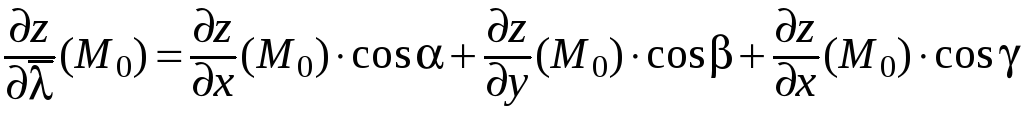