II. Формула для полного приращения

Теорема. Пусть функция удовлетворяет двум условиям:

1. В окрестности точки она имеет частные производные .

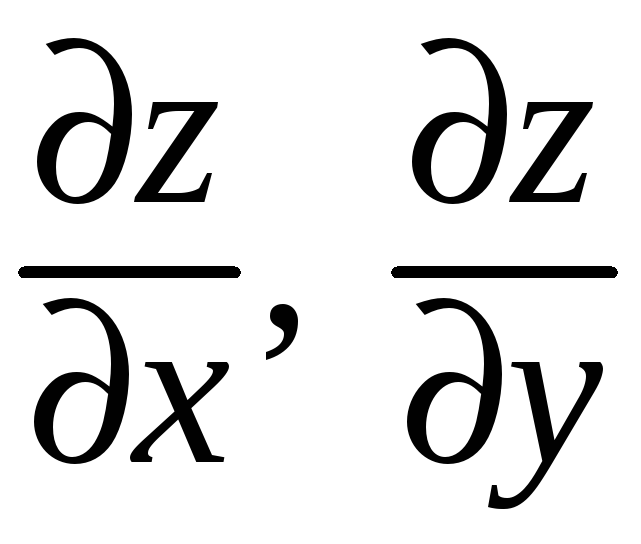2. В самой точке частные производные непрерывны.

Тогда для полного приращения в точке справедлива формула :

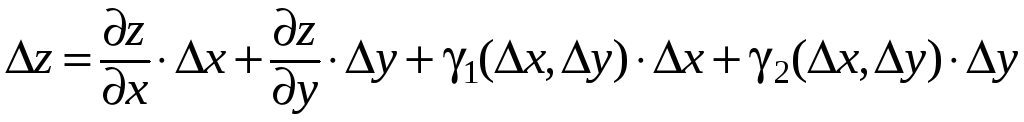, (4)

где частные производные вычислены в точке , а функции являются при и бесконечно малыми величинами.

Доказательство.

(см. рис. 7).

Разность

можно рассматривать как разность двух значений функции

,

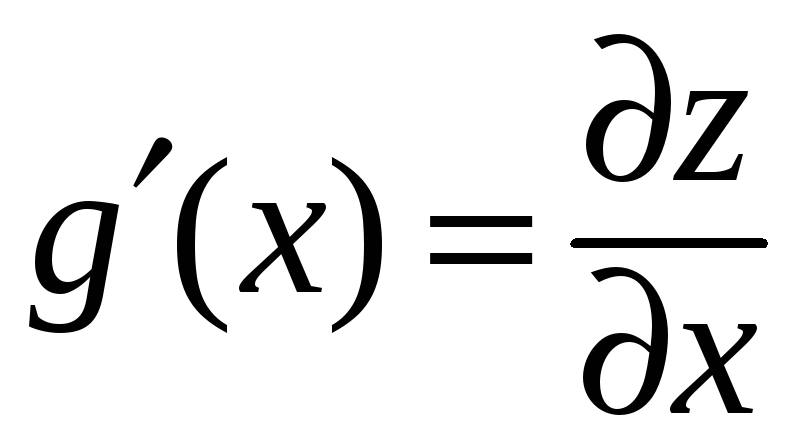зависящей от одной переменной , причем ее производная является частной производной по исходной функции : . По теореме Лагранжа [4]:

,

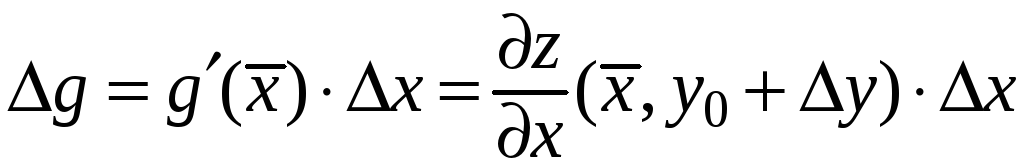где промежуточная точка , и потому .

Аналогично разность

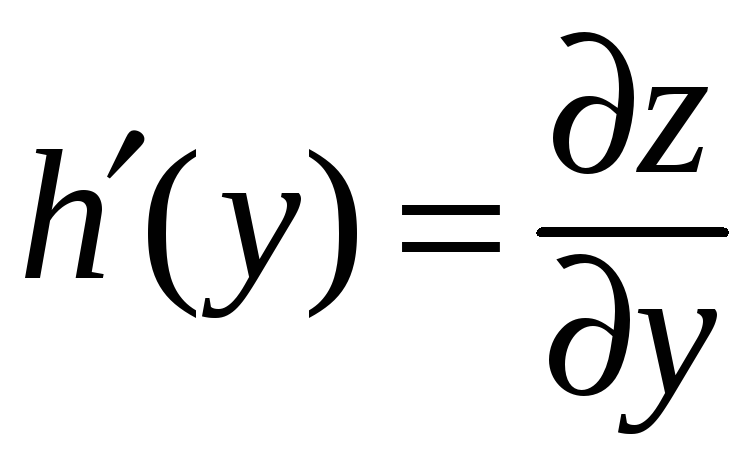можно рассматривать как разность двух значений функции , зависящей от одной переменной , причем ее производная является частной производной по исходной функции : . По теореме Лагранжа:

,

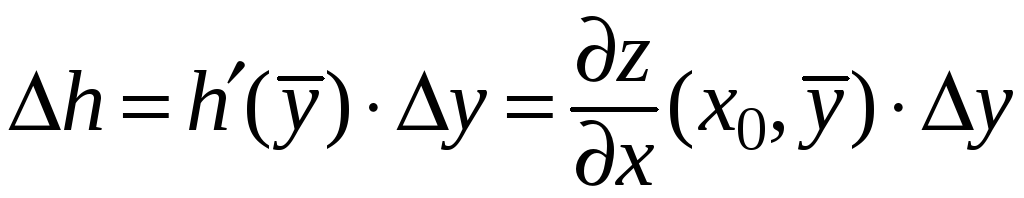где промежуточная точка , и потому .

Итак,

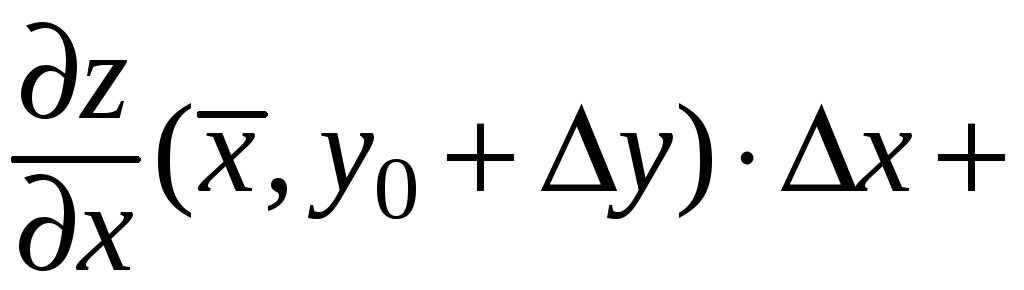
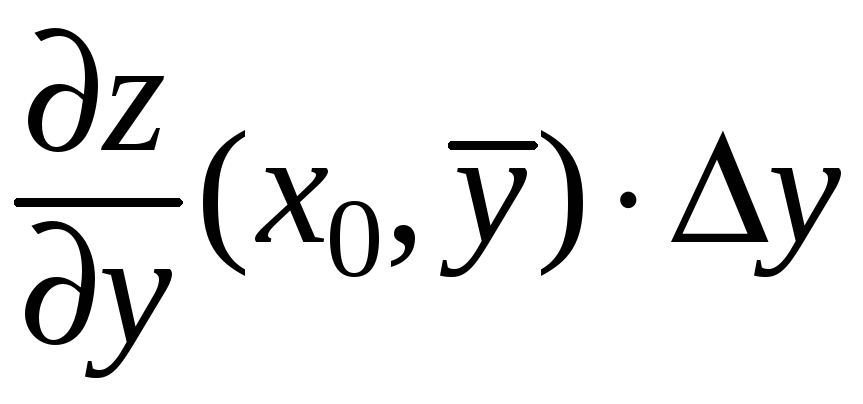. (5)

Воспользуемся теперь непрерывностью частных производных в точке :

.

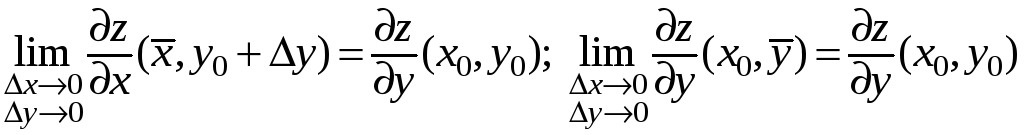Отсюда по теореме о структуре сходящейся переменной [4]):

;

,

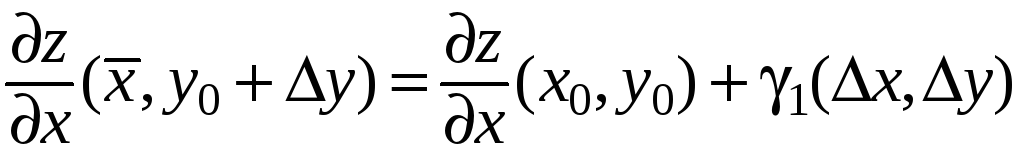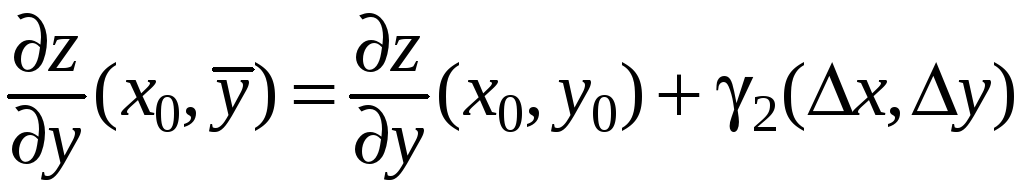где функции являются бесконечно малыми величинами при и . Подставляя эти выражения в (5), получаем (4). ▄

III. Достаточное условие дифференцируемости

Теорема. Пусть функция удовлетворяет условиям предыдущей теоремы:

1. В окрестности точки она имеет частные производные .

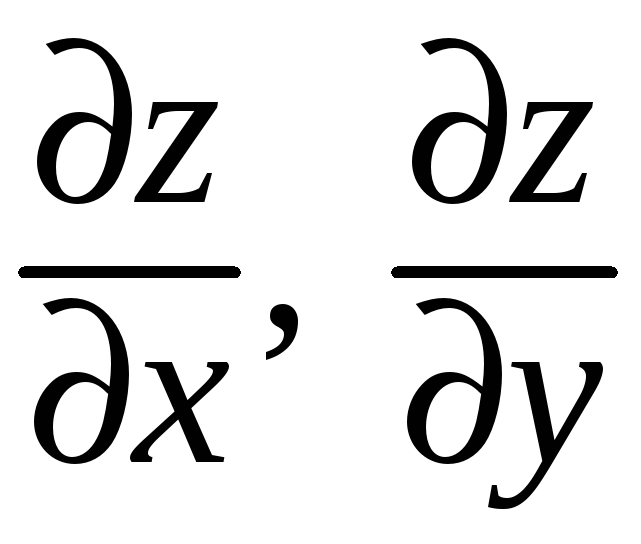2. В самой точке частные производные непрерывны.

Тогда дифференцируема в точке .

Доказательство. В силу условий теоремы справедлива формула (4) для полного приращения :

.

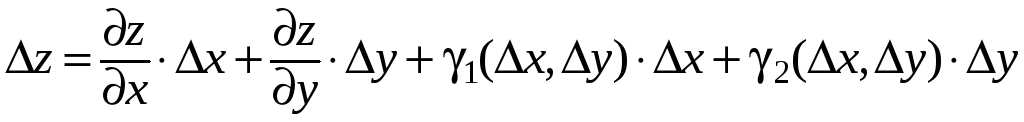Для того, чтобы придти к представлению (2), входящему в определение дифференцируемости, положим

.

Остается убедиться, что функция является бесконечно малой более высокого порядка, чем . Имеем

;

при этом

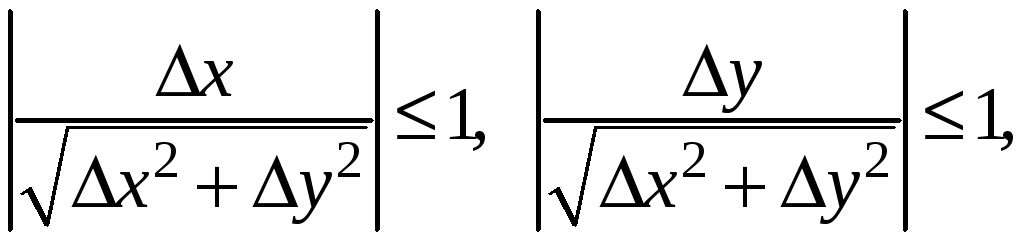
и по свойствам бесконечно малых: 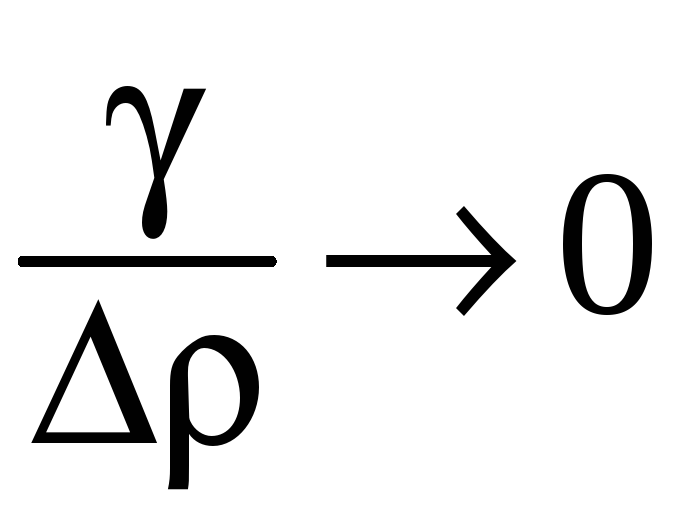при . ▄

IV. Соотношение понятий непрерывности, дифференцируемости и частных производных

Как уже отмечено выше, из дифференцируемости функции нескольких переменных следует ее непрерывность. Здесь сохраняется логическая связь понятий, характерная для функций одной переменных. Однако из одного существования в точке частных производных еще не следуют ни дифференцируемость, ни даже непрерывность функции двух или более переменных. Далее, из непрерывности функции даже при условии существования частных производных не следует ее дифференцируемость. Дело здесь в том, что частные производные характеризуют в случае функции двух переменных ее поведение в малой окрестности точки не полностью, а только в направлениях координатных осей. Приведем соответствующие примеры.

Примеры. 1. Функция непрерывна в точке , но частные производные в этой точке не существуют.

Действительно, непрерывность функции обусловлена непрерывностью элементарных функций. В то же время разностное отношение

не имеет двустороннего предела при , поскольку при оно постоянно и равно , а при постоянно и равно .

2. Функция

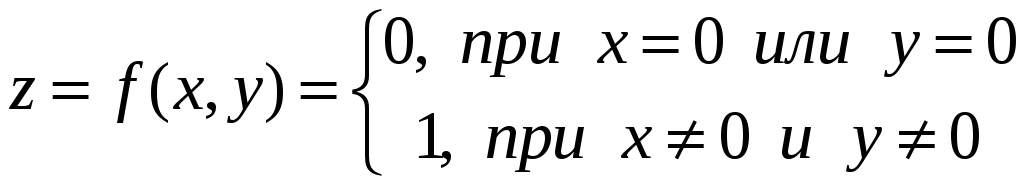
имеет в точке частные производные, но не является в этой точке непрерывной.

Действительно, полагая , имеем , откуда . Аналогично . В то же время предел функции в точке не существует, так как сколь угодно близко от нее существуют как значения, равные (в точках, не лежащих на координатных осях), так и значения, равные (в точках, лежащих на координатных осях).

3. Функция в точке непрерывна, имеет частные производные, но не является дифференцируемой.

Действительно, непрерывность следует из того, что 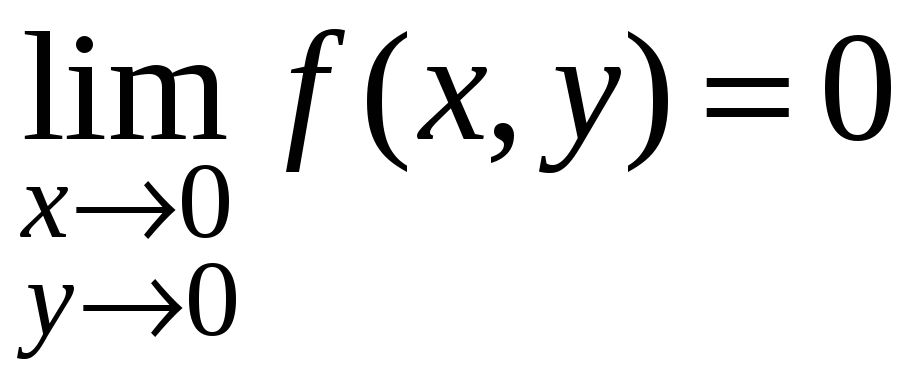, и . Далее,

,

.

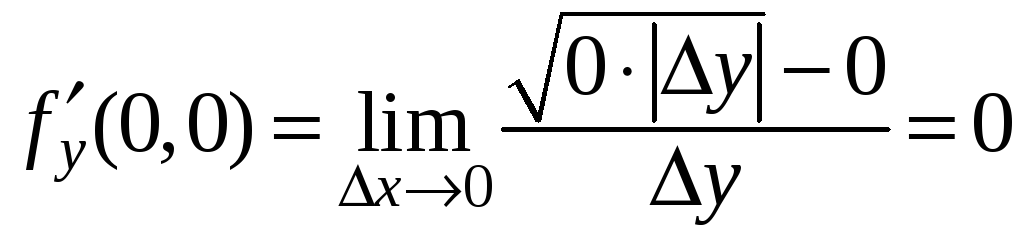В то же время при имеем . Как известно, эта функция не дифференцируема в точке . Если бы теперь была дифференцируема в точке , то при соответствующая функция — а это как раз — также была бы дифференцируема.