
- •1. Понятие функции нескольких переменных
- •I. Понятие окрестности
- •II. Понятие области
- •III. Определение функции
- •5. Частные производные
- •6. Дифференцируемость функции нескольких переменных
- •I. Понятие дифференцируемости
- •II. Формула для полного приращения
- •III. Достаточное условие дифференцируемости
- •IV. Соотношение понятий непрерывности, дифференцируемости и частных производных
- •7. Частные производные сложной функции
- •8. Полная производная сложной функции
- •9. Дифференцирование неявной функции
- •10. Уравнения касательной к пространственной линии
- •Как и в случае плоской кривой, имеет место следующее Определение. Касательной к линии в точке называется предельное положение секущей при .
- •11. Уравнение касательной плоскости и уравнения нормали к поверхности
- •Уравнения нормали к поверхности
- •(Без доказательства).
- •13. Экстремумы
- •Необходимое условие экстремума
- •Определение. Точка области определения функции называется стационарной, если в этой точке существуют частные производные первого порядка, и выполняется необходимое условие экстремума:
- •Достаточное условие экстремума
- •Замечание. Если , то для решения вопроса о наличии экстремума требуется привлечение производных более высоких порядков.
- •14. Производная по направлению и градиент
- •I. Направляющие косинусы вектора
- •II. Понятие производной по направлению
- •III. Понятие градиента
- •IV. Связь производной по направлению с градиентом
- •Литература
- •Ястребов Михаил Юрьевич математика
- •Учебное пособие
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО
ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ
————————————————————————————————
Ястребов М.Ю.
МАТЕМАТИКА
َФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Утверждено Редакционно-издательским советом
университета в качестве учебного пособия
Санкт-Петербург
2006
УДК
ББК
Рецензент:
Кандидат физико-математических наук, доцент
Кузнецов В.О.
Ястребов М.Ю. Математика. Функции нескольких переменных. — Учебное пособие: СПб: СПГУВК, 2006 — 48 С.
Учебное пособие предназначено для студентов первого курса экономических и технических специальностей. Оно соответствует рабочей программе дисциплины «Математика» и может быть использовано как при подготовке к экзамену, так и для текущих учебных занятий.
УДК
ББК
© Санкт-Петербургский государственный
Университет водных коммуникаций, 2006
1. Понятие функции нескольких переменных
I. Понятие окрестности
Н

![]() -окрестностью
точки
-окрестностью
точки
![]() называется совокупность
называется совокупность
![]() точек
точек
![]() ,
удаленных от
,
удаленных от
![]() меньше чем на
меньше чем на
![]() :
:
![]() .
Эта окрестность является интервалом
.
Эта окрестность является интервалом
![]() (рис. 1).
(рис. 1).
Также
и на плоскости
![]()
![]() -окрестностью
точки
-окрестностью
точки
![]() называется совокупность
называется совокупность
![]() точек
точек
![]() ,
удаленных от
,
удаленных от
![]() меньше чем на
меньше чем на
![]() :
:
![]() .
.
Э
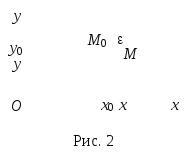
![]() с центром в точке
с центром в точке
![]() (рис. 2).
(рис. 2).
Аналогично
в пространстве
![]()
![]() -окрестностью
точки
-окрестностью
точки
![]() называется совокупность
называется совокупность
![]() точек
точек
![]() ,
для которых
,
для которых
![]() .
.
Эта
окрестность является открытым шаром
(без граничной сферы) радиуса
![]() с центром в точке
с центром в точке
![]() (рис. 3).
(рис. 3).
Р

Рис. 3
II. Понятие области
Определение.
Областью
на плоскости
![]() называется
множество
называется
множество
![]() точек
точек
![]() ,
которое удовлетворяет двум условиям:
,
которое удовлетворяет двум условиям:
1.
Множество
![]() является «цельным», состоящим «из одного
куска» (связным)
в том смысле, что любые две точки из
является «цельным», состоящим «из одного
куска» (связным)
в том смысле, что любые две точки из
![]() можно соединить линией, целиком лежащей
в
можно соединить линией, целиком лежащей
в
![]() .
.
2.
Множество
![]() является открытым:
для любой точки
является открытым:
для любой точки
![]() некоторая ее окрестность целиком
содержится в
некоторая ее окрестность целиком
содержится в
![]() .
.
На рис. 4 и 5 изображены примеры двумерных и трехмерных областей.
III. Определение функции
Определение.
В области
![]() плоскости
плоскости
![]() задана функция
двух переменных
задана функция
двух переменных
![]() если каждой точке
если каждой точке
![]() ставится в соответствие по некоторому
правилу
ставится в соответствие по некоторому
правилу
![]() единственное число
единственное число
![]() .
В этом случае
.
В этом случае
![]() называется областью определения функции
называется областью определения функции
![]() .
.
В
этом случае пишут также
![]() —
функция переменной точки области
—
функция переменной точки области
![]() .
.
Примеры.
1.
![]() .
Здесь областью определения является
вся плоскость
.
Здесь областью определения является
вся плоскость
![]() .
.
2.
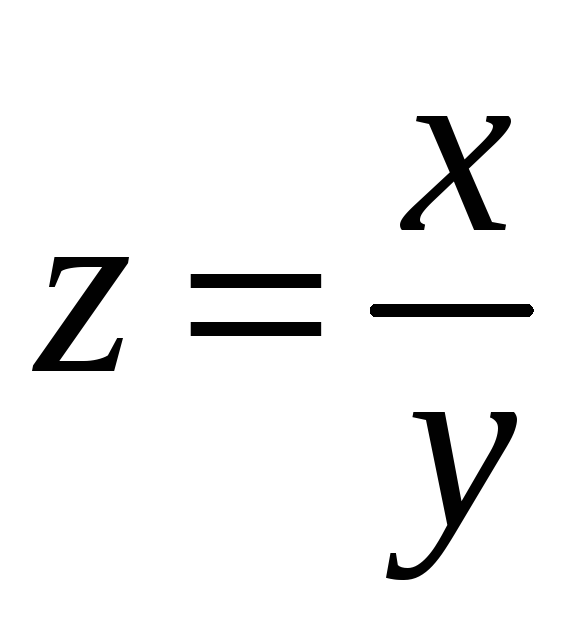 .
Здесь областью определения является
плоскость
.
Здесь областью определения является
плоскость
![]() с выколотой прямой
с выколотой прямой
![]() .
.
Р ис.
4 Рис. 5
ис.
4 Рис. 5
3.
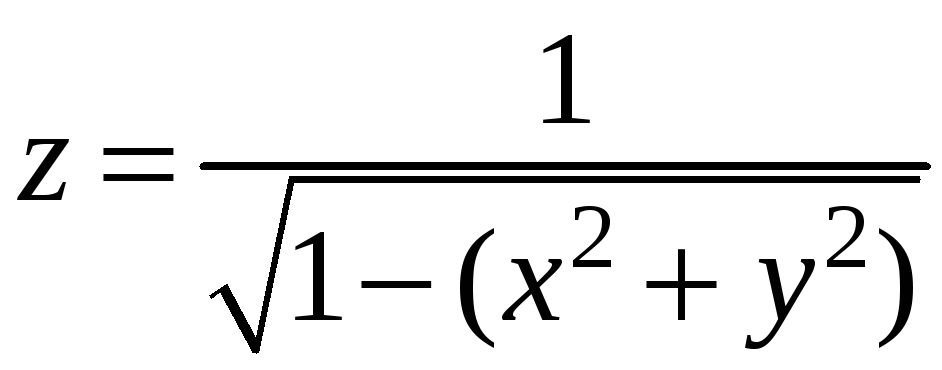 .
Здесь областью определения является
открытый круг радиуса
.
Здесь областью определения является
открытый круг радиуса
![]() с центром в начале координат.
с центром в начале координат.
Аналогично определяется функция трех или более переменных в области пространства трех или более измерений.
Примеры.
1.
![]() .
2.
.
2.
![]() .
.
Определение.
Графиком
функции двух
переменных
![]() является поверхность
является поверхность
![]() в пространстве
в пространстве
![]() ,
состоящая из всех точек пространства
,
состоящая из всех точек пространства
![]() ,
где
,
где
![]() .
.
Проекцией
поверхности
![]() на плоскость
на плоскость
![]() является область определения
является область определения
![]() функции
функции
![]() (рис. 6).
(рис. 6).
Р
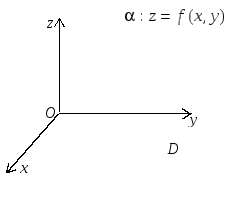
2. Предел функции нескольких переменных
Пусть
точка
![]() является для области определения
является для области определения
![]() функции
функции
![]() внутренней или граничной, так что в
любой ее
внутренней или граничной, так что в
любой ее
![]() окрестности
(то есть сколь угодно близко от нее)
содержатся точки области
окрестности
(то есть сколь угодно близко от нее)
содержатся точки области
![]() .
.
Определение.
Число
![]() называется пределом
функции
называется пределом
функции
![]() в точке
в точке
![]() (говорят также: при
(говорят также: при
![]() или при
или при
![]() ),
если для любого
),
если для любого
![]() (сколь угодно малого) существует
(сколь угодно малого) существует
![]() ,
такое что при выполнении условий
,
такое что при выполнении условий
![]() справедливо неравенство
справедливо неравенство
![]() .
.
Обозначения:
![]() ;
;
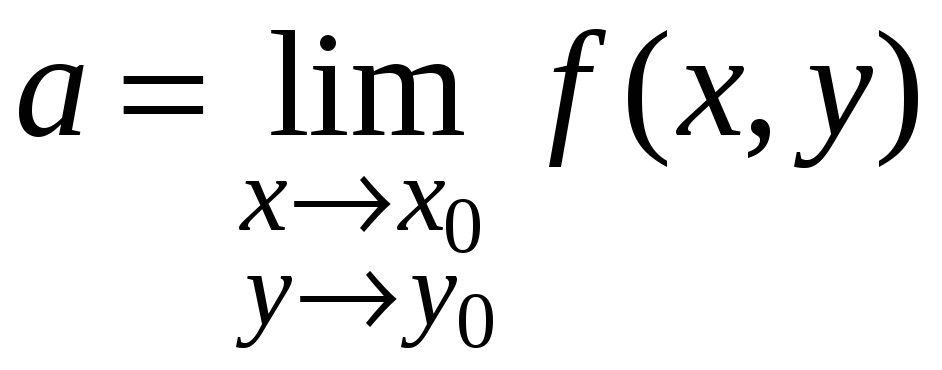 ;
;
![]() ;
;
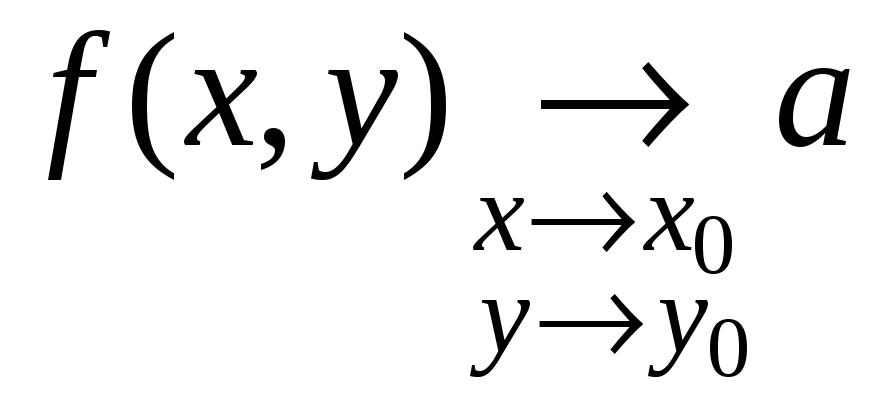 .
.
Аналогично определяется предел функции трех или более переменных.
Замечания.
1.
Геометрически утверждение о том, что
![]() ,
означает, что значения функции
,
означает, что значения функции
![]() сколь угодно близко приближаются к
числу
сколь угодно близко приближаются к
числу
![]() ,
если точка
,
если точка
![]() ,
оставаясь в области определения
,
оставаясь в области определения
![]() ,
достаточно близко подходит к точке
,
достаточно близко подходит к точке
![]() .
.
2. Предел функции нескольких переменных обладает cвойствами, аналогичными свойствам предела функции одной переменной [1]. Мы будем использовать их по мере необходимости.
3. Приращения функции нескольких переменных
Пусть
![]() ― фиксированная
точка области определения
― фиксированная
точка области определения
![]() функции
функции
![]() ,
а приращения
,
а приращения
![]() независимых переменных
независимых переменных
![]() и
и
![]() не выводят переменные точки
не выводят переменные точки
![]() ,
,
![]()
за
пределы
![]() (рис. 7).
(рис. 7).
О
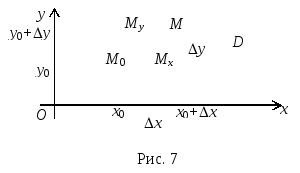
![]() в точке
в точке
![]() называется разность
называется разность
![]() .
.
Для фиксированной
точки
![]() полное приращение
полное приращение
![]() является функцией переменных
является функцией переменных
![]() ,
которая определена при всех достаточно
малых по модулю
,
которая определена при всех достаточно
малых по модулю
![]() .
.
2.
Частным
приращением функции
![]() в точке
в точке
![]() по переменной
по переменной
![]() называется разность
называется разность
![]() .
.
Для фиксированной
точки
![]() частное приращение
частное приращение
![]() является функцией переменной
является функцией переменной
![]() ,
которая определена при всех достаточно
малых по модулю
,
которая определена при всех достаточно
малых по модулю
![]() .
.
Аналогично
частным приращением функции
![]() в точке
в точке
![]() по переменной
по переменной
![]() называется разность
называется разность
![]() .
.
Для фиксированной
точки
![]() частное приращение
частное приращение
![]() является функцией переменной
является функцией переменной
![]() ,
которая определена при всех достаточно
малых по модулю
,
которая определена при всех достаточно
малых по модулю
![]() .
.
Пример.
Рассмотрим функцию
![]() .
Ее полное приращение
.
Ее полное приращение
![]()
![]()
Частные приращения:
![]()
![]()
Если
![]() ,
то в точке
,
то в точке
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Аналогично
определяются полное и частные приращения
функции большего числа переменных.
Например, для функции
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
4. Непрерывность функции нескольких переменных
Пусть
функция
![]() нескольких переменных задана в области
нескольких переменных задана в области
![]() ,
точка
,
точка
![]() принадлежит
принадлежит
![]() .
.
Определение.
Функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если ее предел в этой точке равен значению
функции в самой точке:
,
если ее предел в этой точке равен значению
функции в самой точке:
![]() .
.
Это означает, что
близким к
![]() точкам
точкам
![]() соответствуют близкие к
соответствуют близкие к
![]() значения функции
значения функции
![]() .
.
Определение.
Функция
![]() непрерывна
в области
непрерывна
в области
![]() ,
если она непрерывна в каждой точке этой
области.
,
если она непрерывна в каждой точке этой
области.
Для
функции двух переменных
![]() это геометрически означает, что
поверхность графика функции
это геометрически означает, что
поверхность графика функции
![]() не имеет скачков, разрывов, является
непрерывной в интуитивном смысле.
не имеет скачков, разрывов, является
непрерывной в интуитивном смысле.
Аналогично определяется непрерывность в точке и области для функции большего числа переменных.
Теорема
(критерий непрерывности в терминах
приращений). Для
того, чтобы функция
![]() была непрерывна в точке
была непрерывна в точке
![]() ,
необходимо и достаточно, чтобы бесконечно
малым (стремящимся к нулю) приращениям
независимых переменных
,
необходимо и достаточно, чтобы бесконечно
малым (стремящимся к нулю) приращениям
независимых переменных
![]() и
и
![]() соответствовало бесконечно малое
приращение функции:
соответствовало бесконечно малое
приращение функции:
 .
.
Доказательство. По свойствам предела:
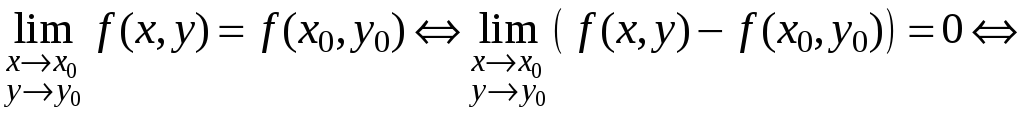
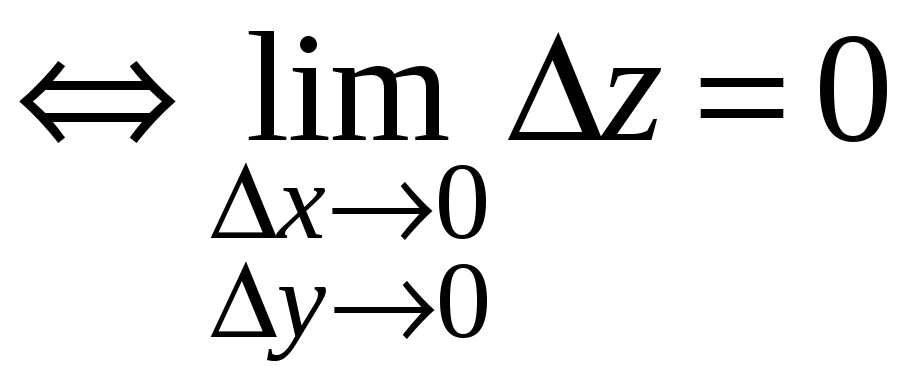 .
▄
.
▄
