2. Элементы векторной алгебры.
1. Вектором
с
началом в точке А
и концом в точке В
называется направленный отрезок.
2. Если
и
,
то координаты вектора равны
или
.
3. Два
вектора
и
равны тогда и только тогда, когда
4. Сумма
векторов
и
есть вектор
.
5. Разность
векторов
и
есть вектор
.
6. Произведение
вектора
на число
есть вектор
.
7. Длина
вектора
есть число
.
8. Единичный
вектор
для вектора
есть вектор
.
9. Скалярное
произведение векторов
и
есть число
,
вычисляемое по формуле:
.
10. Проекция
вектора
на вектор
есть число
.
Аналогично,
.
11. Угол
между векторами
и
вычисляется по формуле:
.
12. Условие
ортогональности двух векторов: векторы
и
ортогональны (
)
тогда и только тогда, когда
или
.
13. Условие
коллинеарности двух векторов: векторы
и
коллинеарные (
)
тогда и только тогда, когда
или
.
14. Направляющие
косинусы вектора
соответственно равны
,
и
,
где ,
,
– углы между вектором
и координатными осями Ox,
Oy
и Oz
соответственно.
15. Векторное
произведение векторов
и
есть вектор
.
16. Длина
векторного произведения
численно равна площади параллелограмма,
построенного на векторах
и
как на сторонах (рис. 5), т. е.
.
Площадь треугольника, построенного на
этих векторах, равна
.
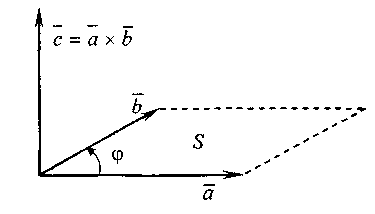
Рис. 5
17. Смешанное
произведение векторов
,
и
есть число
.
18. Условие
компланарности трех векторов: векторы
,
и
компланарны тогда и только тогда, когда
.
19. Смешанное
произведение трех векторов
,
взятое по модулю, численно равно объему
параллелепипеда, построенного на этих
векторах как на ребрах (рис. 6), т. е.
.
Объем пирамиды, построенной на этих
векторах, равен
.
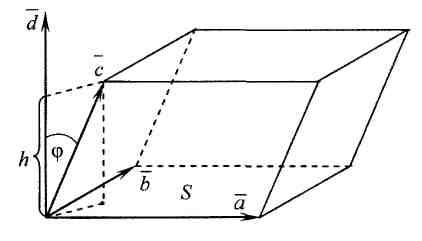
Рис. 6
3. Аналитическая геометрия в пространстве. Различные виды уравнения плоскости
1. Общее
уравнение плоскости:
,
где
– нормальный вектор (ненулевой вектор,
перпендикулярный плоскости).
2. Уравнение
плоскости, проходящей через данную
точку
перпендикулярно данному вектору
(нормальный вектор):
.
3. Неполные уравнения плоскости:
а) 
,
– плоскость проходит через начало
координат;
б) 
,
– плоскость параллельна оси
;
,
– параллельна оси
;
,
– параллельна оси
;
в) 
и
,
– плоскость параллельна координатной
плоскости
;
и
,
– параллельна плоскости
;
и
,
– параллельна плоскости
;
г) 
,
и
,
– определяет координатную плоскость
;
,
и
,
– плоскость
;
,
и
,
– определяет координатную плоскость
.
4. Уравнение
плоскости в отрезках на осях:
,
где a,
b,
c
– величины направленных отрезков,
отсекаемых плоскостью на координатных
осях Ox,
Oy,
Oz
соответственно.
5. Уравнение
плоскости, проходящей через три данные
точки
,
и
:
.
Взаимное расположение двух плоскостей
6. Угол
между плоскостью
с нормальным вектором
и плоскостью
с нормальным вектором
вычисляется по формуле:
.
7. Условие
параллельности двух плоскостей: плоскость
с нормальным вектором
и плоскость
с нормальным вектором
параллельны тогда и только тогда, когда
.
Условие совпадения двух плоскостей:
.
8. Условие
перпендикулярности двух плоскостей:
плоскость
с нормальным вектором
и плоскость
с нормальным вектором
перпендикулярны тогда и только тогда,
когда
.