2. Завдання до самостійної роботи.

1. Згенерувати матрицю суміжностей повного графа (кількість вершин n=5) і знайти мінімальний гамільтоновий цикл методом повного перебору.

2. Згенерувати матрицю суміжностей довільного графа (кількість вершин n=5) і знайти всі гамільтонові шляхи методом повного перебору. Для тестування необхідно розглянути незв’язані і зв’язані графи. Серед зв’язаних графів необхідно розглянути як повні графи, так і неповні.

Звіт

1. Постановка задачі.

2. Хід роботи.

3. Результати роботи.

4. Висновки.

Контрольні питання

1. Який граф називається гамільтоновим? Наведіть приклади.

2. Які є способи представлення графів? Наведіть приклади різних графів та їх представлення. Порівняйте ці способи.

3. Яким є алгоритм пошуку гамільтонового циклу в заданому графі?

4. До якого класу задач можна віднести задачу пошуку гамільтонового циклу в заданому графі?

5. Запишіть реалізацію алгоритму пошуку гамільтонового циклу в заданому графі у вигляді фрагменту Pascal-програми.

Лабораторна робота № 4 Побудова мінімального остовного дерева

Мета роботи: побудувати мінімальне остовне дерево, використовуючи «жадібний» алгоритм.

1. Теоретичні відомості.

Визначення. Остовним деревом зв’язного неорієнтованого графа G=(X, U, F), де X – скінченна множина вершин, U – скінченна множина ребер. F – відношення інцидентності, називається дерево G₀ =(X, U, F). Яке є під графом графа G і містить всі його вершини (рис. 1).

Рис.1 Зв’язний граф і два його остовних дерева

Твердження. Дерево з n вершинами місить n-1 ребро.

Практичне значення остовних дерев дає популярна форма задачі Келі. Необхідно з’єднати n міст залізничними лініями таким чином. Щоб не будувати зайвих доріг. Відома вартість будівництва для кожної пари міст. Якою повинна бути мережа доріг. Що з’єднує всі міста і має мінімальну вартість? Аналогічні питання виникають при проектуванні ліній електропередач, комп’ютерних мереж.

В термінах теорії графів задачу можна сформулювати таким чином. Розглянемо граф G=(X, U, F), де X – міста, U – дороги. Кожному ребру призначимо вагу w(u) – вартість будівництва дороги u. Задача полягає в тому, щоб побудувати зв’язний граф G₀ =(X, U₀, F), який містить всі вершини. З мінімальною вагою . Зрозуміло, що G₀ - дерево, інакше можна було б вилучити одне ребро, не порушуючи зв’язності G₀ і зменшуючи суму вагів його ребер.

Визначення. Мінімальним остовним деревом називають дерево з мінімальною загальною вагою його ребер.

«Жадібний» алгоритм побудови мінімального остовного дерева

Мінімальне остовне дерево графа G=(X, U, F) можна знайти, застосовуючи процедуру дослідження ребер по порядку зростання його ваги. Для цього на кожному кроці вибирається нове ребро з мінімальною вагою, яке не утворює циклу з вже вибраними ребрами. Процес продовжується до тих пір, поки не буде вибране n-1 ребро, де n – кількість вершин графа.. Розглянута процедура називається «жадібним» алгоритмом.

Реалізація даної схеми може бути виконана таким чином. Для кожної вершини графа G=(X, U, F) формуються початкові тривіальні компоненти зв’язності де , , , , i=1, 2, … , |X|. Компоненти Т_і є деревами, об’єднання яких дає початкове наближення шуканого остовного дерева G₀ =(X, U₀, F).

Включення в шукане остовне дерево G₀ вибраного ребра на наступному кроці «жадібного» алгоритму виконується злиттям двох компонент , яким належить по вершині нового ребра, і включенням самого ребра в об’єднану множину ребер. Процес росту об’єднання компонент до остовного дерева G₀ =(X, U₀, F) виконуємо до тих пір, поки не буде включене |X|-1 ребро.

Реалізація «жадібної» схеми формування остовного дерева представлена в алгоритмі 1. Використані для його опису позначення відповідають тим, що вводилися для обґрунтування «жадібної» схеми. Вектор mark[x] міток вершин графа підтверджує їх належність компонентам зв’язності U_i , з яких формується реберний список остовного дерева. Початкові величини mark[x] встановлюються рівними порядковим номерам відповідних вершин. Далі значення mark[x] коректуються по мірі злиття компонент U_i , зберігаючи відповідність належності їм вершин. Початковий граф задається реберним списком U, результуюче остовне дерево також формується реберним списком U₀.

Алгоритм 1. «Жадібний» алгоритм побудови мінімального остовного дерева

for x_i єX do mark[x_i] := i;

Sort (U); {Сортування списку ребер за вагою}

U₀:= 0;

j:=1; {j - індекс даного ребра}

while nU₀<n-1 do

begin

x:= up[j]

y:= uk[j];

if mark[x]<>mark[y] then

begin

U₀ =U₀ U {{x,y)} {Включити ребро в остовне дерево}

nU₀ := nU₀ + 1;

z:= mark[y] {Злиття U_x i U_y }

for i:=1 to n do

begin

if mark[i] = z then mark[i]:= mark[x];

end;

end;

j:=j+1;

end;

Розглянемо приклад побудови мінімального остовного дерева графа, зображеного на мал. 2 , згідно з алгоритмом 1.

• x2 • • x1 x3 • • x4 x5

X1 X2 X3 X4 X5 X1 - 1 8 2 1 X2 1 - 10 7 1 X3 8 10 - 6 5 X4 2 7 6 - 2 X5 1 1 5 2 -

Мал. 2. Граф заданий матрицею вагових коефіціентів

Представимо граф реберним списком, в якому ребра задаються своїми вершинами: одна вершина – в масиві up, а інша – в масиві uk. В масиві f містяться значення вагових коефіцієнтів відповідних ребер.

up	1	1	1	1	2	2	2	3	3	4
uk	2	3	4	5	3	4	5	4	5	5
f	1	8	2	1	10	7	1	6	5	2

Відсортуємо список ребер графа по ваговому коефіціенту в порядку зростання:

up	1	1	2	1	4	3	3	2	1	2
uk	2	5	5	4	5	5	4	4	3	3
f	1	1	1	2	2	5	6	7	8	10

Масив mark[x] містить такі значення:

Mark

1

2

3

4

5

Далі застосуємо «жадібний» алгоритм. На кожному кроці покажемо, як змінюються значення елементів массива mark[x] і як наповнюється новими значеннямимасови ореберного списку остовного дерева dp, dk, df/

• x2 • • x1 x3 • • x4 x5	• x2 • • x1 x3 • • x4 x5
mark 1 1 3 4 5	mark 1 1 3 4 1
dp 1 dk 2 Df 1	dp 1 1 dk 2 5 Df 1 1

а) б)

• x2 • • x1 x3 • • x4 x5	• x2 • • x1 x3 • • x4 x5
mark 1 1 3 1 1	mark 3 3 3 3 3
dp 1 1 1 dk 2 5 4 Df 1 1 2	dp 1 1 1 3 dk 2 5 4 5 Df 1 1 2 5

в) г)

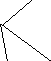
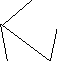
Мал. 3. Побудова мінімального остовного дерева за допомогою «жадібного» алгоритма

Отже, остовне дерево мінімальної довжини представлене на мал.3г). Остовне дерево складається з ребер

,

довжина знайденого остовного дерева дорівнює 9.