2. Завдання до самостійної роботи.

1. Представити десятковий еквівалент множини (у форматі ХХХ - тризначне число, яке задається викладачем) у вигляді двійкового вектора, побудувати двійкову таблицю, отримат аналітичний вираз множини.

2. Відобразити множину за допомогою діаграм Ейлера.

3. Зобразити гіперкуб для множини, яка розглядається.

4. Мінімізувати множину за допомогою методу Квайна.

5. Побудувати діаграму Ейлера для мінімізованої множини. Порівняти з попередньою діаграмою.

Звіт

1. Постановка задачі.

2. Хід роботи.

3. Результати роботи.

4. Висновки.

Контрольні питання

1. Назвати основні аксіоми теорії множин.

2. ,Пояснити поняття конституенти та гіперкуба.

3. Пояснити поняття нормальної форми Кантора множини.

4. В чому полягає метод Квайна мінімізації множин?

Лабораторна робота № 3 Знаходження гамільтонового циклу графа

Мета роботи: знайти мінімальний гамільтоновий цикл заданого повного графа методом повного перебору, знайти всі гамільтонові шляхи довільного графа методом повного перебору,

1. Теоретичні відомості.

Гамільтоновим називається такий шлях у графі, який проходить по кожній вершині лише один раз. На жаль, до сьогодні не існує необхідних і достатніх умов існування гамільтонового шляху в графі. Це питання вивчається вже понад сто років, і відповідь досить не знайдена. Але це говорить лише про те, що не існує оптимальних методів пошуку гамільтонового шляху в графі, однак метод повного перебору завжди дасть правильну відповідь.

Нехай граф заданий матрицею суміжностей. Для визначення існування чи відсутності гамільтонового шляху в заданому графі необхідно переглянути всі варіанти перестановок вершин цього графа. Одночасно з отриманням чергової перестановки цих вершин необхідно перевірити наявність ребер між сусідніми вершинами у ній. У разі розв’язанні задачі про наявність хоча б одного з таких шляхів на цьому можна завершити виконання алгоритму. Якщо треба всі можливі шляхи, необхідно виконати алгоритм перегляду всіх можливих перестановок вершин графа до кінця.

Отже алгоритм пошуку гамільтонового шляху в заданому графі можна сформулювати так.

1. Згенерувати поточну перестановку вершин заданого графа.

2. Розглянути першу пару послідовних вершин у перестановці.

3. Якщо ребро між поточною парою вершин перестановок відсутнє, то перейти до пункту 6.

4. Якщо існує наступна пара послідовних вершин у графі, то перейти до пункту 3.

5. Якщо для всіх пар послідовних вершин існують ребра у графі, то перейти до пункту 7.

6. Якщо існує наступна перестановка вершин заданого графа, то перейти до пункту 1.

7. Вивести вміст перестановок вершин заданого графа, для якого існують усі ребра.

8. Завершити алгоритм.

Нижче наведена реалізація даного алгоритму у вигляді фрагмента Pascal-програми:

flag:=false; {ініціалізація початку роботи алгоритму}

i:=1;

repeat

j:=1; {визначення існування всіх ребер}

while (d[a[j], a[j+1]] = 1) and (j<n) do inc(j); {поточної перестановки вершин}

if j=n then {Якщо така перестановка існує, то}

begin

for j:=1 to n do

write(f_out, a[j], ‘ ‘); {виводимо послідовність вершин.}

{Встановлюємо ознаку існування}

writeln(f_out); {гамільтонового шляху}

flag:=true;

end;

inc(i); {Перехід до наступної перестановки.}

perm; {Визначення наступної перестановки вершин графа}

until (i>=f) or flag; {Завершення пошуку в разі, коли відповідь знайдена або відсутня}

Зауважемо, що змінна f містить значення кількості всіх можливих перестановок вершин графа n! і саме за допомогою лічильника і, який змінюється в межах від 1 до f, ми можемо визначити, чи існує в ньому хоча б один гамільтоновий шлях. Окрім цього, у наведеному фрагменті використано звернення до процедури генерування перестановок.

x₅ x₁ x₃

● ● ●

● ● ●

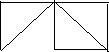x₆ x₄ x₂

	X1	X2	X3	X4	X5	X6
X1	0	1	1	1	1	1
X2	1	0	1	1	0	0
X3	1	1	0	0	0	0
X4	1	1	0	0	0	0
X5	1	0	0	0	0	1
X6	1	0	0	0	1	0

Мал.. 1

Виконавши описаний вище алгоритм для графа, зображеного на малюнку 1, отримаємо результат:

3 2 4 1 5 6

Якщо дещо модифікувати наведений фрагмент програми і визначити всі можливі гамільтонові шляхи розглянутому прикладі графа, то отримаємо таку відповідь:

3 2 4 1 5 6

3 2 4 1 6 5

4 2 3 1 5 6

4 2 3 1 6 5

5 6 1 3 2 4

5 6 1 4 2 3

6 5 1 3 2 4

6 5 1 4 2 3

Розглянемо частинний випадок задачі знаходження гамільтонового шляху, а саме, задачу знаходження мінімального гамільтонового циклу у повному зваженому графі методом повного перебору. Постановка задачі передбачає існування гамільтонового циклу, але необхідно знайти мінімальний цикл, тобто вибрати такий цикл, сумарне значення вагових коефіцієнтів ребер якого - мінімальне число.

Нижче наведена реалізація даного алгоритму у вигляді фрагмента Pascal-програми:

min:=100;

mi:=1; mj:=1; mk:=1; ms:=1; mt:=1;

for i:=1 to 5 do

for j:=1 to 5 do

for k:=1 to 5 do

for s:=1 to 5 do

for ti:=1 to 5 do

begin

if (i< >j) and (i< >k) and (i< >s) and (i< >t) and (j< >k) and

(j< >s) and (j< >t) and (k< >s) and (k< >t) and (s< >t) then

begin

p:=a[i,j]+a[j,k]+a[k,s]+a[s,t]+a[t,i];

if p < min then

begin

min:=p;

mi:=i; mj:=j; mk:=k; ms:=s; mt:=t;

end;

end;

end;