
- •Передмова
- •Лабораторна робота № 1 Множини. Генерація елементів множини та виконання операцій над множинами
- •1. Теоретичні відомості.
- •2. Завдання для самостійної роботи.
- •Варіанти завдань
- •Контрольні питання
- •Лабораторна робота № 2 Мінімізація зображення множин
- •1. Теоретичні відомості.
- •2. Завдання до самостійної роботи.
- •Контрольні питання
- •Лабораторна робота № 3 Знаходження гамільтонового циклу графа
- •1. Теоретичні відомості.
- •2. Завдання до самостійної роботи.
- •Контрольні питання
- •Лабораторна робота № 4 Побудова мінімального остовного дерева
- •Теоретичні відомості.
- •«Жадібний» алгоритм побудови мінімального остовного дерева
- •2. Завдання до самостійної роботи.
- •Контрольні питання
- •Лабораторна робота № 5 Знаходження максимального потоку транспортної мережі
- •Теоретичні відомості.
- •2. Завдання до самостійної роботи.
- •Контрольні питання
- •Лабораторна робота № 6 Визначення найкоротшого шляху в графі
- •Теоретичні відомості.
- •2. Завдання до самостійної роботи.
- •Контрольні питання
- •Лабораторна робота №7 Використання графів в мережі планування.
- •1. Теоретичні відомості.
- •Завдання до самостійної роботи.
- •Контрольні питання
- •Література
2. Завдання для самостійної роботи.
Для самостійної роботи пропонується виконання наступного завдання.
-
Задана універсальна множина X={1, 2, 3, ..., 40}. Необхідно задати множини А, В, С Х, тобто множини, які складаються з натуральних чисел з діапазону від 1 до 40, причому |A|=|B|=|C|=20. Задаються множини шляхом генерації елементи цих множин за допомогою генератора випадкових величин на мові програмування, запропонованій викладачем.
-
Виконати дії над множинами і роздрукувати результати за наданим викладачем варіантом.
Приклад виконання.
Нехай згенеровані на ЕОМ множини А, В, С складаються з елементів: А={1, 3, 4, 5, 10}, B={3, 5, 7, 8, 9}, C={3, 5, 6, 9, 10}.
Тоді результат виконання операції перетину цих множин має вигляд:
D=ABC={3, 5}
Варіанти завдань
-
 . 11.
. 11.
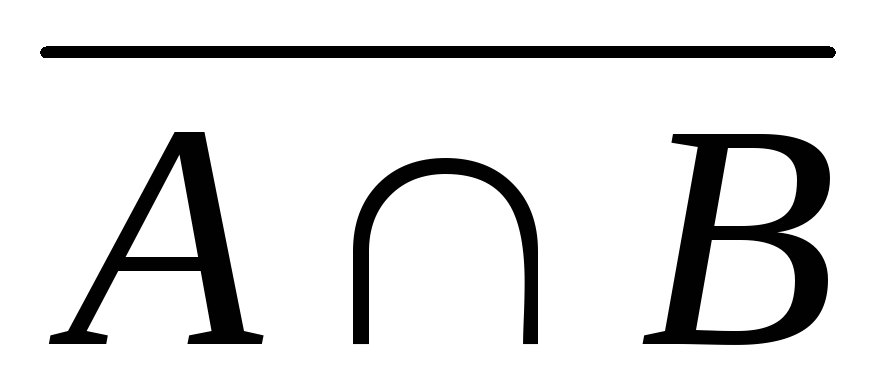 С.
С. -
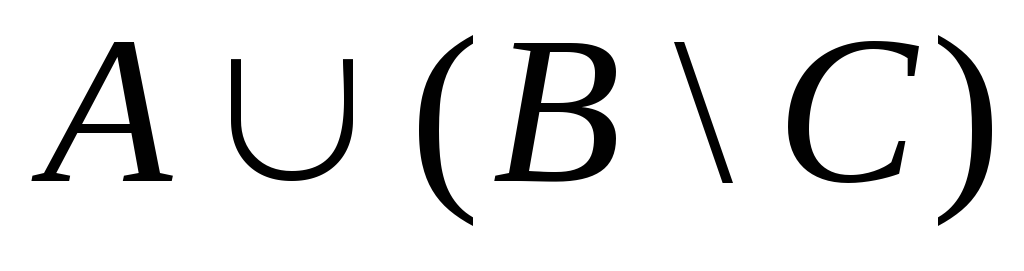 . 12.
. 12.
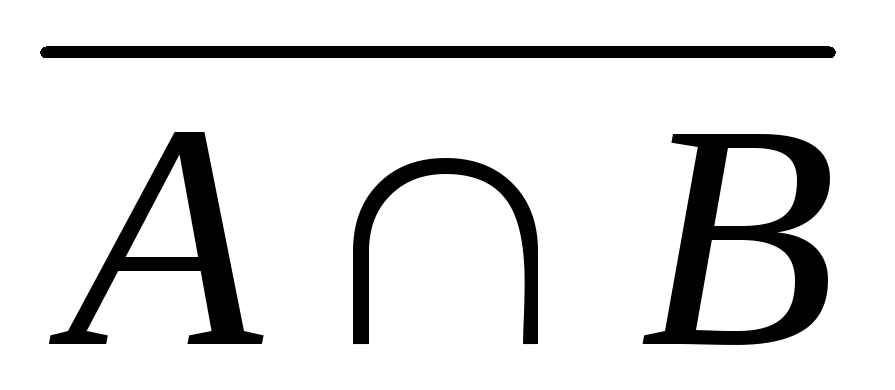 С.
С. -
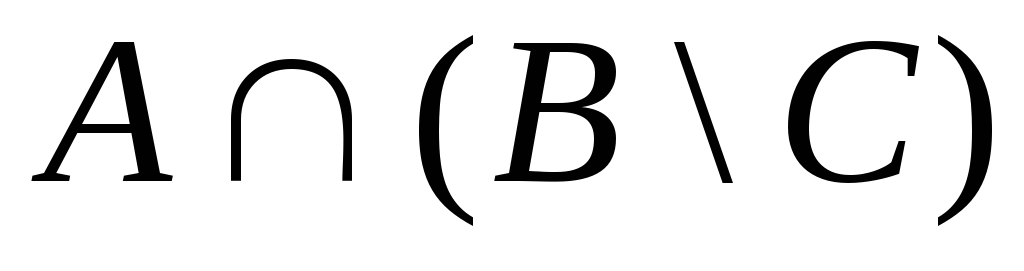 . 13.
. 13.

-
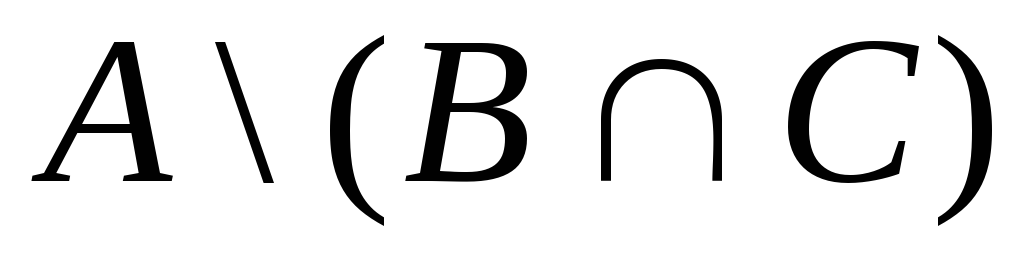 . 14.
. 14.
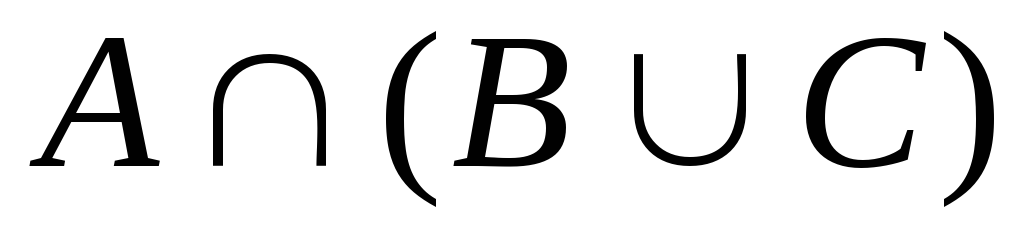
-
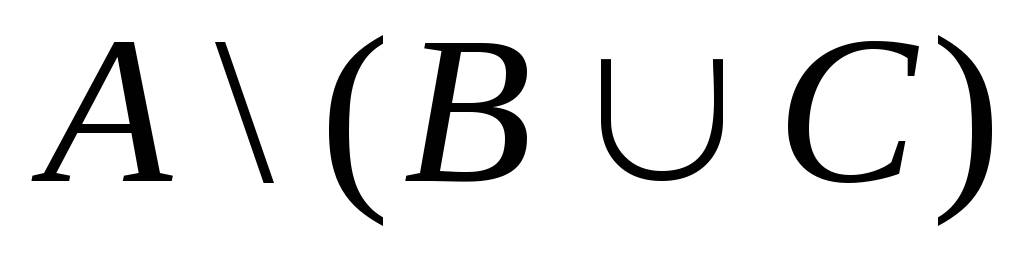 . 15.
. 15.
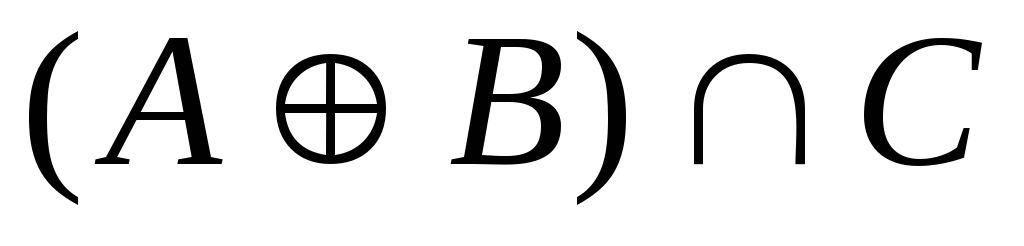 .
. -
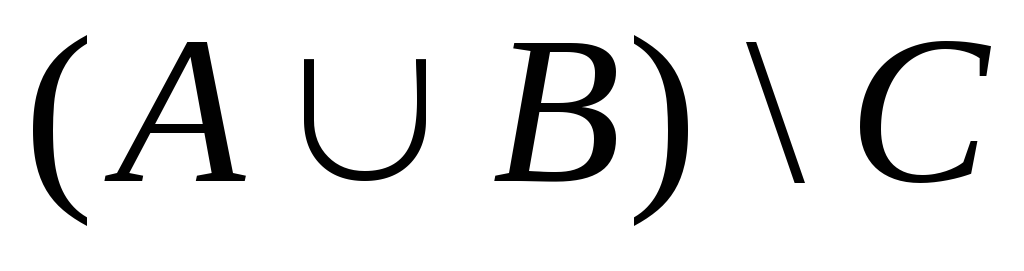 . 16.
. 16.
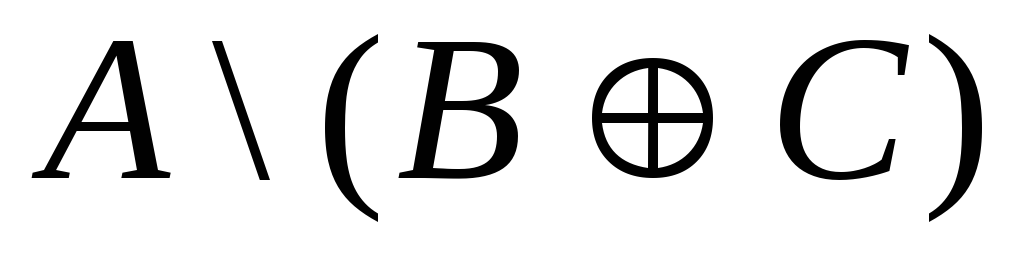 .
. -
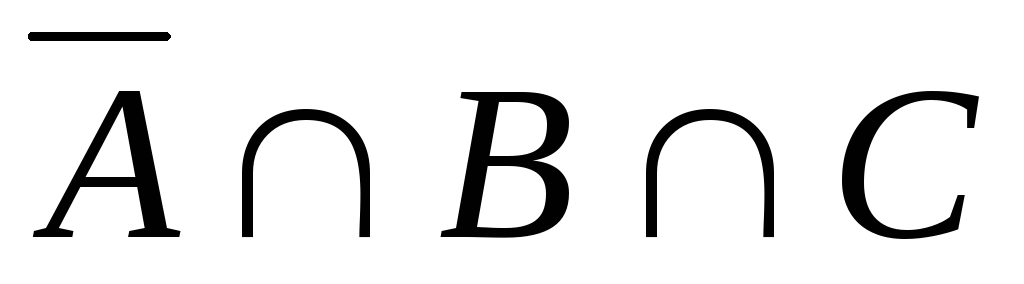 . 17.
. 17.
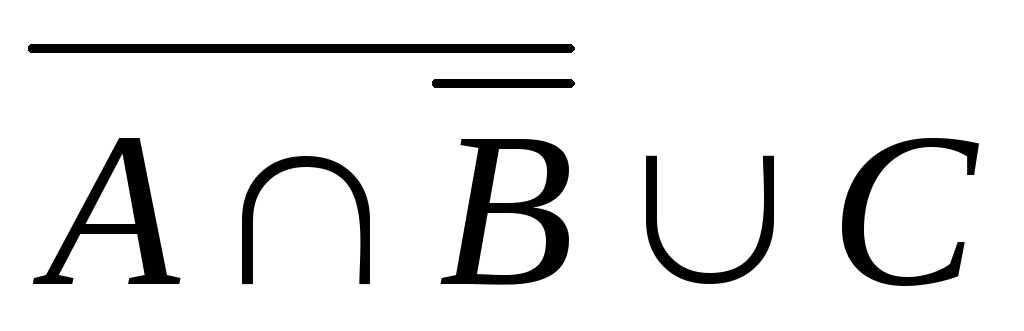 .
. -
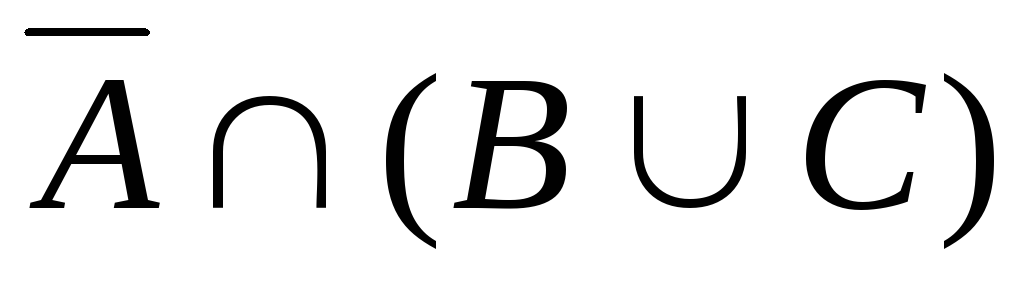 . 18.
. 18.
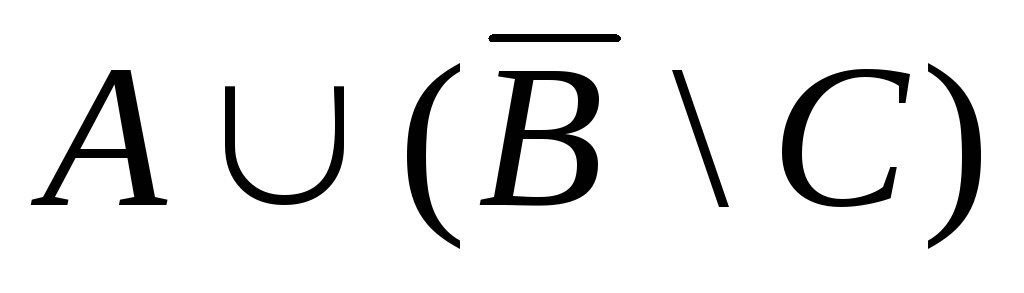 .
. -
.
 . 19.
. 19.
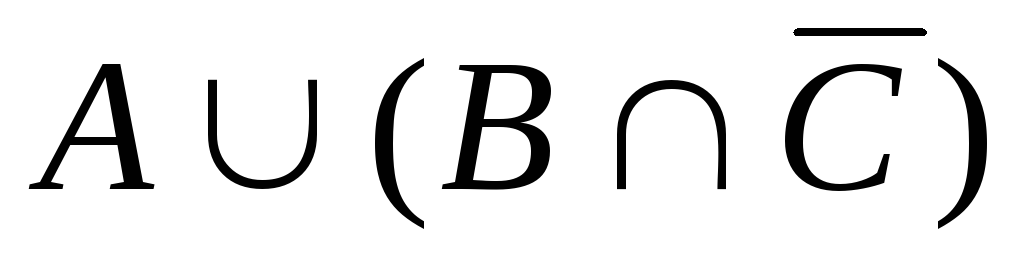 .
. -
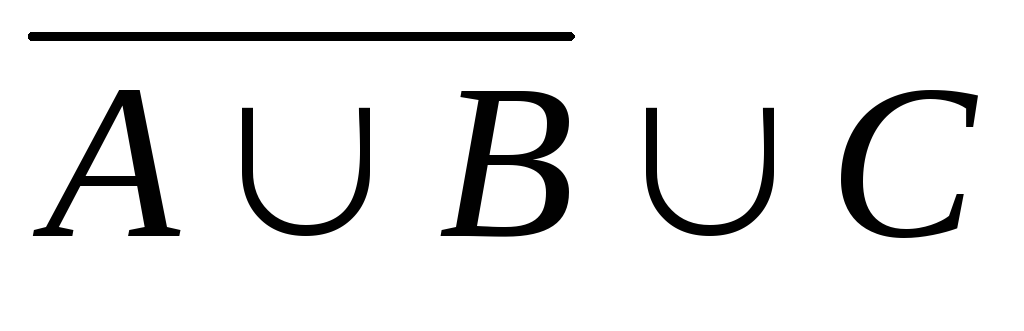 . 20.
. 20.
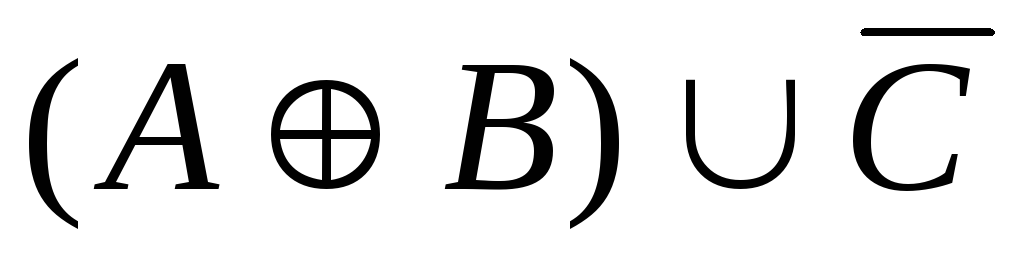 .
.
Примітка. Вважати універсальною множиною Х всі натуральні числа від 0 до 40. Розрахунки виконати використовуючи ЕОМ.
Звіт
-
Постановка задачі.
-
Хід роботи.
-
Лістінг програми.
-
Результати розрахунків та відповіді на поставлені питання.
-
Висновки.
Контрольні питання
-
Основні аксіоми теорії множин.
-
Способи задання множин.
-
Операції над множинами, основні властивості операцій.
-
Загальні операції над множинами.
Лабораторна робота № 2 Мінімізація зображення множин
Мета роботи: Вивчити метод Квайна і на практичному прикладі за його допомогою мінімізувати надану множину.
1. Теоретичні відомості.
Використовуючи аксіоматичний підхід, можливо формально збудувати теорію множин на основі таких аксіом.
-
Аксіома існування.
Існує зокрема одна множина, при цьому в загальному випадку ця множина може бути пустою.
-
Аксіома еквівалентності.
Якщо множини А і В складені з одних і тих самих елементів, то вони співпадають (еквівалентні): А=В.
-
Аксіома об’єднання.
Для не еквівалентних множин А і В (АВ) існує множина С, яка не еквівалентна множинам А і В (СА, СВ), елементами якої є всі елементи множин А і В та в якій не міститься ніяких інших елементів. Множина С називається об‘єднанням множин А і В: С=АВ.
-
Аксіома різниці.
Для деяких множин А і В існує множина С, елементами якої є ті і тільки ті елементи множини А, які не є елементами множини В. Множина С називається різницею множин А і В: С=А\В.
-
Аксіома існування пустої множини.
Існує така множина , якій не належить жодний елемент.
-
Аксіома степені.
Для кожної непустої множини А існує родина множин В(А), елементами якої є всі підмножини Аі множини А, Аі А.
На основі шести введених аксіом базуються операції і поняття теорії множин, які вже були розглянуті (лабораторна робота №1).
Використовуючи основні закони множин, можна розглянути задачу мінімізації складності їх представлення. Послідовність використання цих законів будемо називати стратегією перетворення. Складність представлення множин, які одержуються в результаті використання цих законів, залежить від використаної стратегії. Знайдемо стратегію, яка завжди породжує мінімальний вираз заданої множини. Для цього введемо деякі поняття.
Визначимо множини, які можуть бути утворені з довільних підмножин М1, М2, ..., Мn, які називають утворюючими універсальний простір Х за допомогою операцій , , .
Множину
![]() i=1,
2, ..., n,
i=1,
2, ..., n,
називають первинним термом. Множину виду
![]() ,
,
називають конституентою.
Загальна кількість різних конституент не перевищує 2n. Кожній конституенті можна скласти двійковий набір довжиною n, кількість таких наборів дорівнює 2n. Якщо деякі конституенти дорівнюють , то загальна кількість їх менше ніж 2n, при цьому серед підмножин знайдуться хоча б дві таких, які можна виразити одне через друге, тобто незалежні.
Лема 1. Перетин двох різних конституент пусто.
Лема 2. Об’єднання всіх конституент дорівнює Х.
Крім цього треба відмітити два важливих моменти:
-
кожна непуста множина, яка утворена з множин М1, М2, ..., Мn за допомогою операцій , , , є об’єднанням деякого числа конституант;
-
з n множин можна утворити не більш ніж
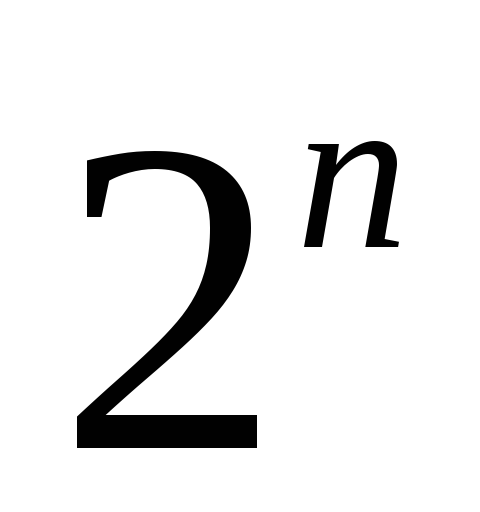 підмножин.
підмножин.
Введення поняття конституенти дозволяє задавати множину М при фіксованих незалежних підмножинах М1, М2, ..., Мn універсальної множини Х у вигляді об’єднання конституент:
![]() .
.
Кожна
фіксована множина МіХ
розділяє простір на дві частини: на Мі
та
![]() .
При незалежних множинах Мi{Mi
|
i=1,...,n}
простір розділяється на 2*2*...*2=2n
областей. Кожна з них є перетином n множин
Мі
або
.
При незалежних множинах Мi{Mi
|
i=1,...,n}
простір розділяється на 2*2*...*2=2n
областей. Кожна з них є перетином n множин
Мі
або
![]() .
Цим областям можна поставити двійковий
вектор (1,
2,...,
n),
в якому і=1,
якщо в перетин
.
Цим областям можна поставити двійковий
вектор (1,
2,...,
n),
в якому і=1,
якщо в перетин
![]() входить
Мі
та
і=0,
якщо входить
входить
Мі
та
і=0,
якщо входить
![]() ,
а також десятковий еквівалент
,
а також десятковий еквівалент
![]() .
.
Розглянемо, наприклад, в тривимірному просторі Х={M1, M2, M3} множину М(M1, M2, M3) с десятковим еквівалентом d(M)=186. В двійковому вигляді можемо записати:
18610=1*27+0*26+1*25+1*24+1*23+0*22+1*21+0*20.
Тоді множині М відповідає двійковий вектор (1, 0, 1, 1, 1, 0, 1, 0), який визначає включення областей в множину М (див. табл.1).
Табл.1.
|
Розряд /число/ |
М1 |
М2 |
М3 |
М |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
0 |
|
7 |
1 |
1 |
1 |
1 |
Аналітичний вираз для множини М:
![]()
Ця множина має 18 символів і може бути проілюстрована за допомогою діаграм Ейлера на мал.1 (заштрихована область).
Х 111
М1 1-1
4 -11
110
6 7 5 011 -01 101 10-
0 -1
-1
2 3 1 100
М2 М3 001
010
000
Мал.1. Діаграми Ейлера. Мал.2. Гіперкуб.
Крім діаграм Ейлера простір може бути заданий у вигляді гіперкуба або n - мірного куба (n - розмірність простору, яка дорівнює кількості фіксованих множин).
Гіперкубом (n - мірним кубом) називається граф H, кожна вершина якого взаємно-однозначно відповідає області простору, та дві вершини з’єднанні ребром, якщо вони відповідають сусіднім областям (мають спільну границю). Зіставлені цим областям двійкові вектори відрізняються тільки в одному розряді.
Для розглядає мого прикладу гіперкуб приведений на мал.2.
Розглянемо
задачу мінімізації представлення множин
в алгебрі Кантора. Перетин попарно
різних множин
![]() називають
елементарним.
Вираз, що задає множину Мi
у вигляді об’єднання різних елементарних
перетинів, називають нормальною
формою Кантора
(НФК) множини
М. Об’єднання конституент множини М
називають досконалою
НФК множини
М. Мінімальною
НФК
множини
М називається НФК цієї множини, яка має
мінімальну складність.
називають
елементарним.
Вираз, що задає множину Мi
у вигляді об’єднання різних елементарних
перетинів, називають нормальною
формою Кантора
(НФК) множини
М. Об’єднання конституент множини М
називають досконалою
НФК множини
М. Мінімальною
НФК
множини
М називається НФК цієї множини, яка має
мінімальну складність.
Розглянемо метод Квайна, який будемо використовувати для побудови мінімальною НФК множини М. Цей метод полягає в послідовному виконанні таких кроків.
-
Виділення максимальних інтервалів. Інтервалом множини М називаються множини конституент множини М, які утворюють гіперкуб (деякої розмірності).
-
Будують таблицю Квайна. Це двовимірна таблиця, де кожному рядку відповідає ребро, а кожному стовпцю - вершина (конституента), які використовуються в гіперкубі для заданої множини. В таблиці ставиться 1 на перетині i-го рядка та j-го стовпця, якщо j-та вершина з’єднана з i-тим ребром.
-
Будують покриття таблиці Квайна. Покриттям таблиці Квайна називається множина рядків, для кожного стовпця яких знайдеться хоча б один рядок з цієї множини, на перетині з яким цей стовпець має одиницю. Причому при викреслюванні хоча б одного рядка ця властивість не виконується.
В розглянутому прикладі таблиця Квайна має вигляд:
|
Максимальний інтервал |
Конституента |
||||
|
|
001 |
011 |
100 |
101 |
111 |
|
0-1 |
1 |
1 |
|
|
|
|
-01 |
1 |
|
|
1 |
|
|
-11 |
|
1 |
|
|
1 |
|
10- |
|
|
1 |
1 |
|
|
1-1 |
|
|
|
1 |
1 |
Максимальний інтервал називається обов’язковим, якщо знайдеться конституєнта, яка належить йому і тільки йому. Множина обов’язкових інтервалів утворює ядро покриття.
В нашому випадку ядром покриття є максимальний інтервал {10-}, який покриває третій та четвертий стовпець. Для створення покриття достатньо вибрати перший та третій рядок, або перший та п’ятий, або другий та третій, тобто маємо три варіанти покриття:
-
{10-; 0-1; -11},
-
{10-; 0-1; 1-1},
-
{10-; -01; -11},
кожний з яких має вже не 18 а 6 елементів НФК.
Мінімальна НФК є результатом знаходження всіх варіантів покриття таблиці Квайна та виконання над отриманими множинними виразами тотожних перетворень:
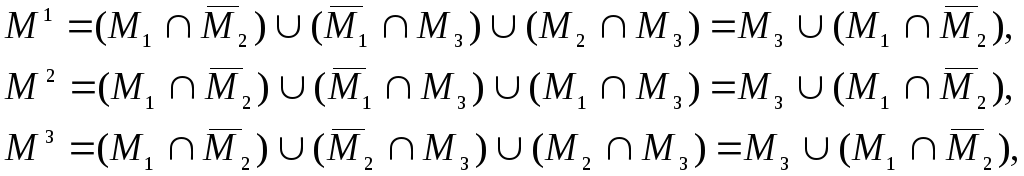
Таким чином, отримали мінімізовану множину М, яка еквівалентна одній з М1, М2, М3.
Задача мінімізації зображення множин має велике прикладне значення, тому що її розв’язання дозволяє задавати логічні функції з використанням мінімальної кількості елементів, що є одним з показників при проектуванні цифрових пристроїв, так як дозволяє збільшити їх надійність, швидкість, компактність.
