Методические указания и контрольные работы по Математическим методам финансового анализа в условиях определенности

1.Основные понятия и методы финансовых вычислений

1.1. Основные понятия математики, используемые в финансовых вычислениях

Процент – это одна сотая доля величины. Тысячная доля называется промилле. Величина а в процентах от величины b рассчитывается по формуле:

А рифметическая и геометрическая прогрессии – широко используются в финансовых вычислениях, поэтому напомним их определения:

Прогрессия – последовательность чисел а₁, а₂, …, а_n,…, построенная по определенным правилам.

Арифметическая прогрессия – это числовая последовательность, для которой разность любых двух соседних чисел есть величина постоянная.

Любой член последовательности находится по формуле:

a_n= a₁+d(n-1),

где d-разность арифметической прогрессии,

n-порядковый номер элемента последовательности.

Сумма арифметической прогрессии находится по формуле:

.

Геометрическая прогрессия – это числовая последовательность, для которой отношение любых двух соседних чисел есть величина постоянная.

Любой член последовательности находится по формуле:

a_n= a₁*q^n-1,

где q-знаменатель геометрической прогрессии,

n-порядковый номер элемента последовательности.

Сумма возрастающей геометрической прогрессии находится по формуле:

.

Сумма убывающей геометрической прогрессии находится по формуле:

.

Пример 1.1. Пусть S=1000руб. – это первоначальный вклад в банк, на которые начисляются простые проценты по ставке r =10%. Найти последовательность наращенных сумм за n=3 промежутка начисления.

Решение.

Дано a1=S=1000 r=0,1	Решение Искомая последовательность есть арифметическая прогрессия с начальным членом a1=S=1000, n=4, знаменателем (разностью) арифметической прогрессии d= S*r =1000*0,1=100. Тогда при n=1 a1=1000; при n=2 a2= a1 + d (n-1)=1000 + 100*1=1100; при n=3 a3=1000+100*2=1200; a4=1000+ 100*3=1300.
Найти S1=?=1100 S2=?=1200 S3=?=1300

Пример 1.2. Господин N старается спланировать должным образом приближающийся выход на пенсию. Брокер по ценным инвестиционным бумагам предложил схему, согласно которой господин N платит крупную сумму фирме, а в обмен получает гарантированный ежемесячный доход в 300 дол. Более того, каждый месяц доход будет увеличиваться на 40 дол. Какова будет ситуация через пять лет?

Решение.

Дано: a1=300, n=60, d=40 Найти: a60=?=2660 дол.

Решение. Найти величину дохода, который через 5 лет получит господин N за месяц: a60=300 +(60-1) *40=2660 дол. Найти общий доход за 5 лет:

1.2. Экономическая теория процента

Часто используемый финансовый показатель – это процентная ставка (проценты), которая представляет собой процентное выражение дохода от величины денежного вклада (например, инвестиции, кредитования). Выплаты процентов вызваны следующими основными причинами: потеря потенциальной полезности денег и неопределенность относительно стоимости денег через какой – то промежуток времени. Действительно, деньги являются только средством обмена, напрямую они не удовлетворяют наши жизненные потребности, так как не являются пищей, одеждой, едой и т.д. Чтобы принести пользу, их обменивают на другие товары и услуги, которые и удовлетворяют жизненные потребности. В том случае, когда деньги инвестированы или отданы в долг, они теряют свою потенциальную полезность. Кроме того, отдавая деньги на некоторый период, кредиторы рискуют своим благосостоянием. Для компенсации этой потери и служит процент.

И так, процентная ставка r_t = i + f + E_p +g(t) определяется следующими слагаемыми:

• i – норма процента, отражающая компенсацию кредитору за отказ использовать в других целях предоставленную сумму в течение времени t (пока не вернут долг).

• f – фактор риска (эффект Фишера) – компенсация кредитору за неопределенность (риск) неполучения процентов или всей суммы вообще при наступлении срока возврата долга.

• E_p – инфляционная добавка, т.е. компенсация за возможные изменения в уровне цен, за уменьшение покупательной способности денег вследствие инфляции.

• g(t) – компенсация за продолжительность срока t, на который ссужены деньги – чем больше срок, тем больше компенсация.

На сегодняшний день существует большое разнообразие процентных ставок. Они отличаются по методам вычисления, по величине, а также могут быть как постоянными (фиксированными), так и изменяющимися в определенные промежутки времени. Факторы, определяющие эти ставки можно разделить на 2 группы: которые определяют общий уровень процентных ставок и те, которые определяют различие процентных ставок.

Факторы, влияющие на уровень процентных ставок:

• политика правительства

• денежная масса

• ожидания относительно будущей инфляции.

Факторы, влияющие на различие процентных ставок:

• время до погашения финансовых обязательств

• риск невыполнения обязательств

• ликвидность финансовых обязательств

• налогообложение

• другие различные факторы, специфические для конкретных финансовых обязательств, например, предоставлено ли обеспечение активами, включены ли права выбора в договор.

В следующей таблице приведены процентные ставки, соответствующие разным финансовым инструментам или рынкам в конце декабря 1995 года.

Таблица 1. Процентные ставки (%), декабрь 1995

№	Процентные ставки, соответствующие различным финансовым инструментам и ли рынкам	%
1	Ипотечная ссуда	7,85
2	Банковский депозит с недельным сроком извещения о снятии средств	4,5
3	Банковский овердрафт	22,0
4	Трехмесячный банковский депозитный сертификат	6,375
5	Трехмесячный коммерческий вексель	6,45
6	Трехмесячный казначейский вексель английского правительства	6,32
7	Шестимесячный межбанковский кредит	6,34
8	Государственная облигация со сроком погашения 5 лет (Великобритания)	7,0
9	Государственная облигация со сроком погашения 10 лет (Великобритания)	7,4
10	Государственная облигация со сроком погашения 10 лет (Германия)	5,88
11	Корпоративная облигация со сроком погашения 5 лет, обеспеченная активами корпорации (Великобритания)	8,1
12	Корпоративная облигация со сроком погашения 5 лет, не обеспеченная активами корпорации (Великобритания)	9,2
13	Конвертируемая облигация со сроком погашения 5 лет (Великобритания)	6,5

Но можно выделить два основных метода вычисления результативности сделки с помощью понятия ставки:

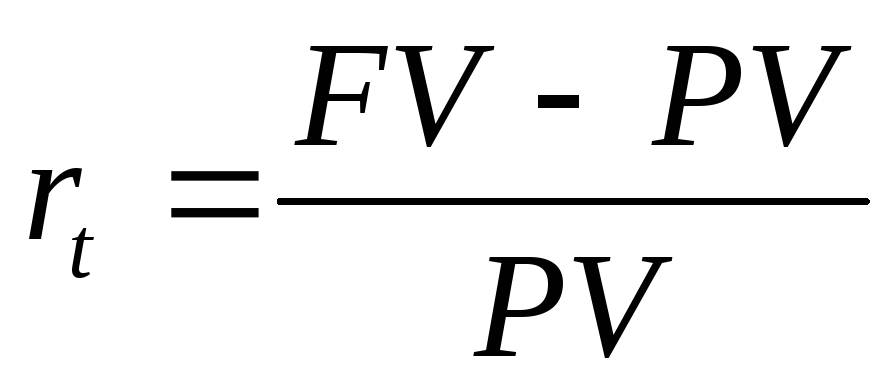1. , где r_t – называют процентная ставка, ставка процента, процент, рост, норма прибыли, доходность и

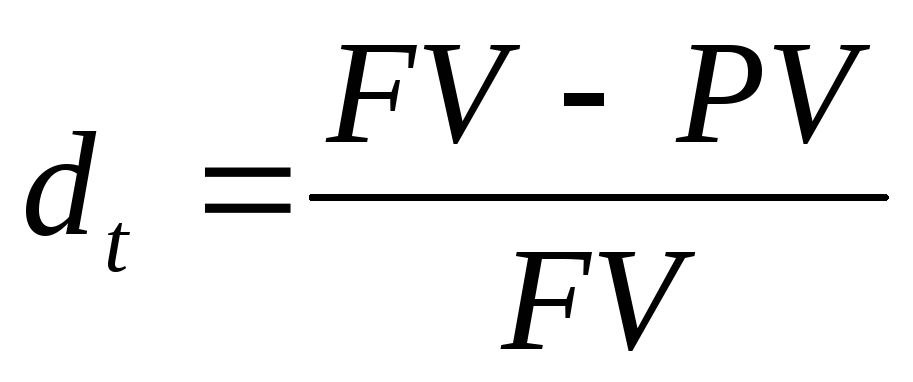2. , где d_t – учетная ставка; PV- текущая современная стоимость капитала (present value); FV- будущая наращенная стоимость капитала (future value).

Рассмотрим некоторые количественные свойства этих ставок. Процентная ставка r_t, как следует из ее определения, должна быть положительной r_t>0, а d_t – учетная ставка должна быть положительной, но меньше единицы 0<d_t<1. Связь между r_t и d_t определяется следующими соотношениями: . Очевидно, что d_t < r_t, но d_t < 1, тогда d_t < min(r_t, 1). Эти неравенства позволяют сделать более точную оценку ставки d_t по известной ставке r_t.

Так как 0<d_t<1, то справедливо Поэтому Если d_t достаточна мала, то r_t  d_t.

Следующая величина, оценивающая результативность сделок – это дисконт фактор, который показывает, какую часть сумма PV составляет в сумме FV:

Индекс роста В_t суммы PV за время t показывает, во сколько раз изменилась (увеличилась) первоначальная сумма за время t:

Таким образом, индекс роста показывает, во сколько раз за данный период выросла величина капитала по отношению к величине капитала в конце предыдущего периода. Если известны индексы за последовательные периоды времени , то за время индекс роста В_t=