2.5. Уравнение Лагранжа

Уравнение вида

, (2.26)

в котором у является линейной функцией от х с коэффициентами, зависящими от , причем коэффициент при х не равен , называется уравнением Лагранжа. Построение его общего решения в параметрической форме сводится к интегрированию линейного уравнения.

Положим , где р – параметр, тогда уравнение (2.26) принимает вид:

. (2.27)

Заменив в равенстве величину dy ее значением из (2.27), а вместо подставим р:

или

. (2.28)

Уравнение (2.28) можно привести к линейному уравнению с искомой функцией х, если разделить обе его части на dp и . После выполнения этих действий, получим

. (2.29)

Поскольку уравнение (2.29) линейно относительно х и и, следовательно, легко интегрируется, например методом вариации произвольной постоянной. Получив интеграл Ф(х,р,С) = 0 уравнения (2.29) и присоединяя к нему уравнение (2.27), получим

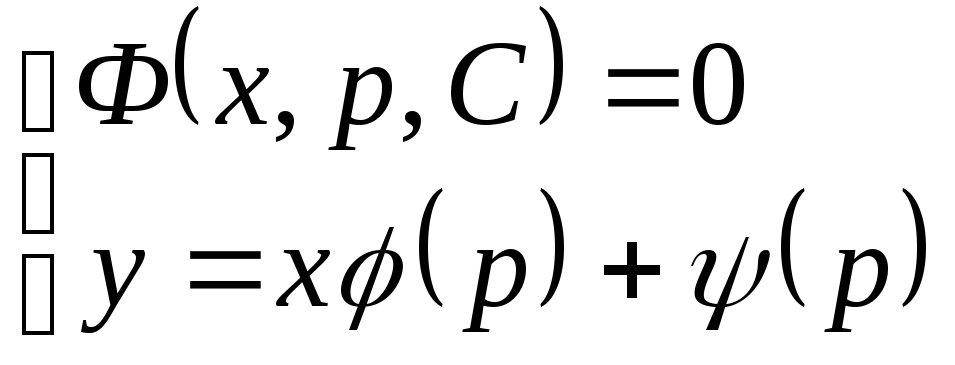. (2.30)

Эти уравнения определяют искомые интегральные кривые.

При переходе от уравнения (2.28) к уравнению (2.29) пришлось делить на . Но при этом мы потеряли решения, если они существуют, для которых р постоянно, а значит . Считая р постоянным, замечаем, что уравнение (2.28) удовлетворяется лишь в том случае, когда р является корнем уравнения

. (2.31)

Итак, если уравнение (2.31) имеет действительные корни , то к найденным выше решениям уравнения Лагранжа надо добавить еще

. (2.32)

Эти прямые линии могут оказаться особыми решениями уравнения Лагранжа.

Пример 41. Найти решения уравнения: .

▲Полагая в этом уравнении , будем иметь

.

Дифференцируя обе части этого уравнения по р, получим

подставляя р = 0 в равенство , находим у = 0.Это также является решением исходного уравнения, и притом частное.▲

Пример 42. Найти решения уравнения: .

▲Полагая в этом уравнении , будем иметь

или .

Продифференцируем это равенство:

Производя замену , приходим к уравнению:

Отсюда, сокращая на р, получаем уравнение с разделяющимися переменными:

или .

Интегрируя это уравнение, получим:

или .

Подставив это уравнение в , получим: .

При сокращении на р мы потеряли особое решение; полагая р = 0, находим из данного уравнения у = 0: это и есть особое решение.

Следовательно,

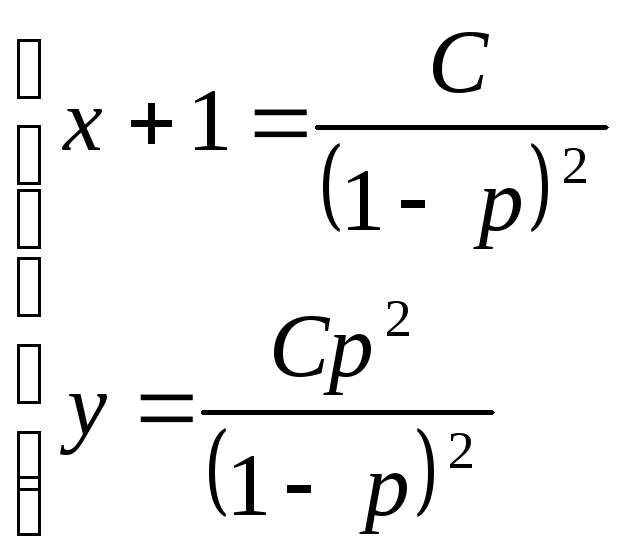- общее решение исходного уравнения,

а у = 0 – особое решение.

В общем решении параметр р можно исключить и привести его к виду:

.▲

2.6. Уравнение Клеро

Уравнение вида

, (2.33)

называется уравнением Клеро. Оно отличается от уравнения Лагранжа только тем, что в нем коэффициент при х равен .

Полагая , где р – параметр, получим:

. (2.34)

Дифференцируя по х, будем иметь:

или , (2.35)

откуда

,

или

.

В первом случае, исключая р, получим

(2.36)

- однопараметрическое семейство интегральных кривых.

Во втором случае решение определяется уравнениями

и . (2.37)

Нетрудно проверить, что интегральная кривая, определяемая уравнениями (2.37), является огибающей семейства прямых (2.36).

Действительно, огибающая некоторого семейства Ф(х,у,С) = 0 определяется уравнениями

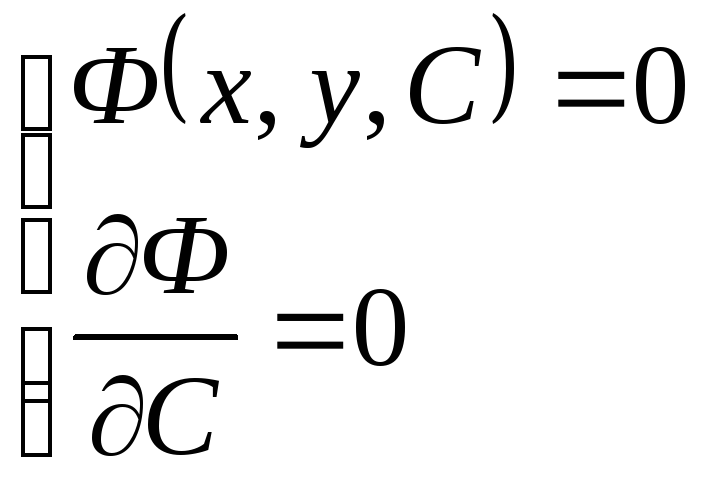, (2.38)

которые для семейства (2.36) имеют вид

, ,

и лишь обозначением параметра отличаются от уравнений (2.37).

Пример 43. Найти решения уравнения: .

▲Это уравнение Клеро. Полагая в этом уравнении , будем иметь:

.

Отсюда:

или

.

Наконец,

.

Это уравнение может выполняться для функций двух видов:

1. Для таких функций у(х), для которых dp = 0, т.е. функций вида:

у =Сх+С₁.

Но не все линейные функции этого вида удовлетворяют данному уравнению, а лишь те, которые имеют вид:

.

Это есть общий интеграл исходного уравнения Клеро (он получается из уравнения простой заменой на С).

2. Уравнение выполняется и для таких функций у(х), для которых выполняется тождество

.

Присоединяя это уравнение к уравнению , мы также получаем решение исходного уравнения:

,

которое будет особым решением.

Исключение р из этой системы, приводит к уравнению:

Если общее решение выражает однопараметрическое семейство прямых, то особое решение выражает равнобочную гиперболу. Эта гипербола служит огибающей семейства прямых .▲

Пример 44. Найти решения уравнения: .

▲Введем параметр, обозначая , тогда исходное уравнение будет иметь вид:

.

Выразим у через р для чего из последнего равенства выразим dx, используя равенство :

.

Следовательно,

.

Интегрируя последнее уравнение, получим

.

Равенства и совместно выражают в параметрической форме общее решение исходного уравнения Клеро:

. ▲