Задачи для самостоятельной работы

Решить уравнения

10. . 21. .

22. . 23. .

24. . 25. .

Решить задачи Коши.

26. . 27. .

28. . 29. .

30. .

Проинтегрировать уравнения и, где указано, решить задачу Коши.

31. . 32. .

33. . 34. .

35. .

36. .

Найти общее решение уравнений, имеющих частные решения вида

37. . 38. .

39. .

1.6. Уравнения в полных дифференциалах

1. Рассмотрим уравнение вида

, (1.83)

будет называться уравнением в полных дифференциалах, если существует такая функция u=u (x,y), что ее полный дифференциал совпадает с левой часть уравнения (1.83), т.е.

. (1.84)

С другой стороны полный дифференциал функции u=u (x,y) равен

, (1.85)

поэтому из выражений (1.84) и (1.85) следует выполнение тождеств

и . (1.86)

Необходимым и достаточным условием существования функции u=u(x,y) (при существовании непрерывных частных производных первого порядка от функций М(х,у) и N(x,y)), является выполнение тождества

, (1.87)

которое называется условием Эйлера.

Если же условие (1.87) выполняется, то функция u=u(x,y) определяется по формуле:

,(1.88)

или же в виде:

. (1.89)

В этой формуле можно брать произвольно, лишь бы точка оставалась в области где М(х,у) и N(x,y) и их частные производные были бы непрерывны.

Итак, если левая часть уравнения (1.83) совпадает с полным дифференциалом функции u=u(x,y), то справедливо выражение

или du = 0 . (1.90)

Следовательно, функция u=u(x,y) является общим интегралом уравнения (1.83), т.е

u(x,y) = C, (1.91)

а с учетом (1.88) общий интеграл уравнения (1.83) можно вычислить по формуле

С, (1.92)

или с учетом (1.89), по формуле

С . (1.93)

Общий интеграл уравнения (1.83) можно также найти, используя равенства (1.86). Для этого сначала потребуем, чтобы выполнялось равенство , отсюда найдем функцию u(x,y):

, (1.94)

где y) – произвольная дифференцируемая функция от у, а при выполнении интегрирования переменную у под знаком интеграла надо считать постоянной.

Теперь из множества функций u(x,y) выделим ту, которая удовлетворяет условию . Функция u(x,y,) определяемая из (1.94), будет удовлетворять этому условию, если будет выполняться равенство

,

или

,

то есть функция y) должна иметь вид:

. (1.95)

Подставив (1.95) в равенство (1.94), получим искомую функцию u(x,y), а, следовательно, и общий интеграл уравнения (1.83):

.(1.96)

Для получения формулы (1.96) мы потребовали, чтобы выполнялось равенство . Однако, можно потребовать, чтобы в первую очередь выполнялось равенство и, проводя аналогичные рассуждения, придем к уравнению

,(1.97)

которое так же, как и уравнение (1.96) определяет общий интеграл уравнения (1.83).

Пример 27. Найти общий интеграл уравнения:

.

▲Установим, является ли исходное равнение уравнением в полных дифференциалах. Для этого проверим, выполняется ли условие Эйлера (1.87). Здесь

, а .

Вычислим производные и : и , следовательно, условие Эйлера выполнено, и исходное уравнение является уравнением в полных дифференциалах. Найдем функцию u(x,y) по изложенной выше схеме, а именно, предположим, чтобы выполнялось равенство :

,

отсюда

.

Далее потребуем от u(x,y) обеспечения равенства :

,

или , или . Следовательно, .

Таким образом, искомая функция и соответственно общий интеграл исходного уравнения будут иметь вид:

.

Получим общий интеграл исходного уравнения, потребовав выполнения равенства :

, а теперь потребуем, чтобы выполнялось : . Найдем . Таким образом, общий интеграл исходного уравнения имеет вид:

.

Следовательно, независимо от того, какое из условий (1.86) будет выполняться в первую очередь, общий интеграл исходного уравнения будет одним и тем же.

Общий интеграл исходного уравнения можно записать в виде (1.89):

.

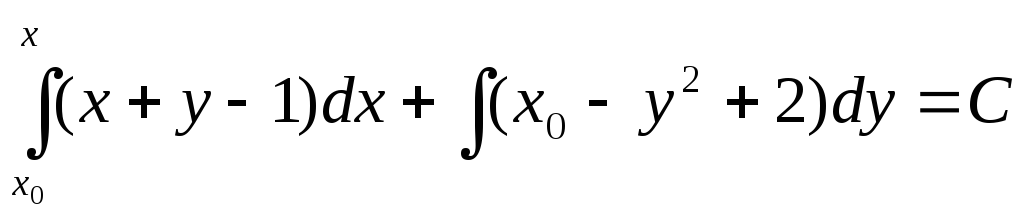Выполним интегрирование:

,

или

,

т.к. можно брать произвольно, то, обозначив , окончательно получим

.▲

2. Если мы вновь обратимся к уравнению (1.83): , то можем отметить, что для него не всегда выполняется условие Эйлера (1.87):

.

Несмотря на этот факт, в некоторых случаях удается достаточно просто подобрать некую функцию (x,y) так, чтобы после умножения на нее левая часть уравнения (1.83) обращается в полный дифференциал, т.е. уравнение

уже является уравнением в полных дифференциалах и выполняется тождество:

.

Такая функция (x,y) называется интегрирующим множителем для данного уравнения и определяется из уравнения

,

которое можно переписать в виде:

. (1.98)

Если заранее известно, что , где  -заданная функция от х и у, то уравнение (1.98) сводится к обыкновенному (и притом линейному) уравнению с неизвестной функцией от независимой переменной:

, (1.99)

где - 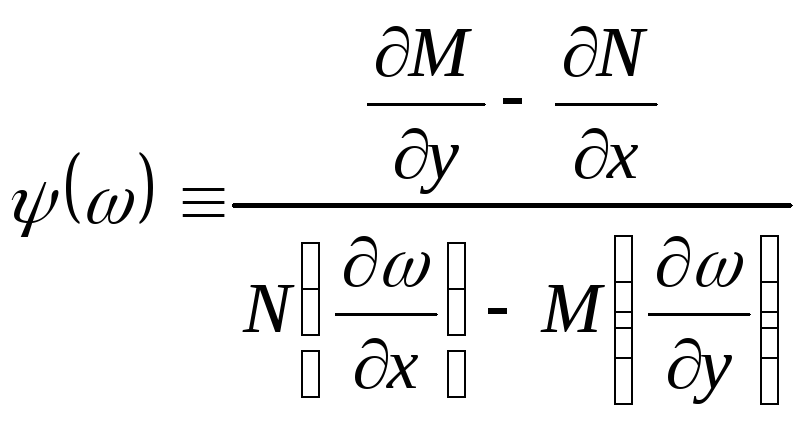(1.100)

т.е. дробь справа является функцией только от  .

Решая уравнение (1.99), находим интегрирующий множитель

.

В частности, уравнение (1.83) будет иметь интегрирующий множитель, зависящий только от х (= х) или только от у (= у), если выполнены соответствующие условия:

, (1.101)

или

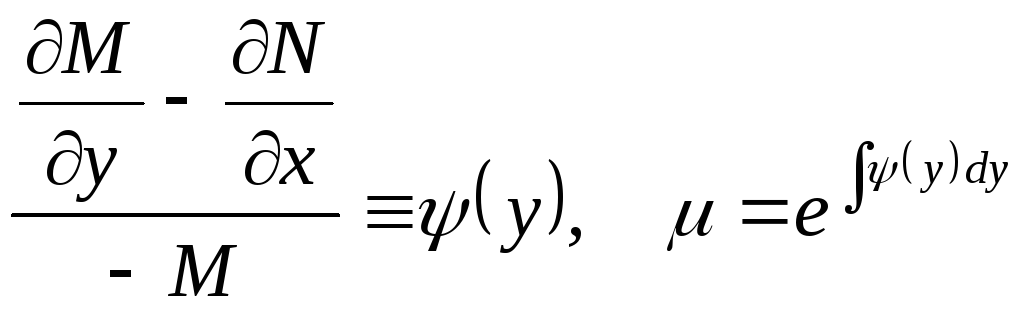. (1.102)

Пример 28 . Найти общий интеграл уравнения:

.

▲Определим, является ли это уравнение уравнением в полных дифференциалах. Проверим, выполняется ли условие Эйлера. Для этого вычислим частные производные от по у, и от по х:

,

следовательно, условие Эйлера не выполнено и исходное уравнение не является уравнением в полных дифференциалах.

Проверим, существует ли для этого уравнения интегрирующий множитель, зависящий только от х? Для этого проверим условие (1.101):

.

Следовательно, ответ на поставленный вопрос положителен, и можно определить интегрирующий множитель:

.

Таким образом, умножив исходное уравнение на этот множитель, мы приведем его к уравнению в полных дифференциалах:

. ()

Проверив еще раз условие Эйлера, установим:

.

Результат проверки свидетельствует о том, что полученное уравнение () является уравнением в полных дифференциалах. Найдем общий интеграл уравнения ().

,

.

Таким образом, общий интеграл исходного уравнения имеет вид:

.▲

Пример 29. Найти общий интеграл уравнения:

.

▲Это уравнение не является уравнением в полных дифференциалах, т.к.

Проверим, имеет ли это уравнение интегрирующий множитель зависящий только от у: (у).

Действительно, проверим условие (1.102):

Следовательно, .

После умножения исходного уравнения на , получим уравнение

,

которое будет являться уравнением в полных дифференциалах, т.к.

.

Следовательно, интегрируя последнее уравнение, будем иметь:

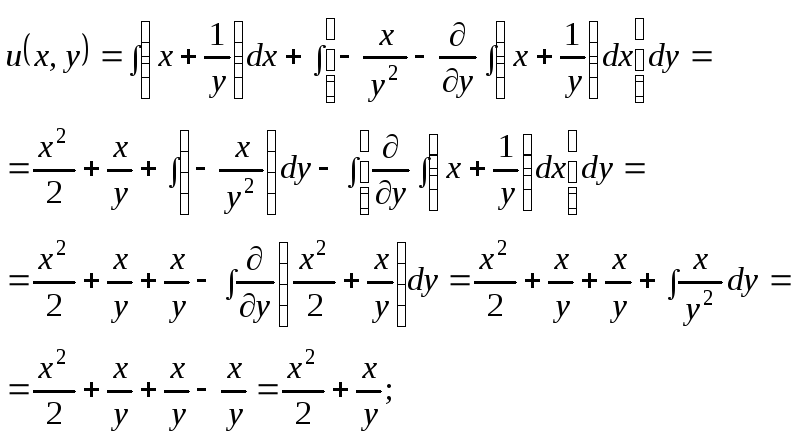
Таким образом, общий интеграл исходного уравнения будет иметь вид:

.▲

Пример 30. Найти общий интеграл уравнения:

.

▲ Проверка условия Эйлера для этого уравнения показала, что оно не выполняется:

.

Достаточно просто убедиться о том, что это уравнение не имеет интегрирующих множителей, зависящих только от х и только от у:

и

В этом случае предположим, что в (1.99) равно: . Тогда и уравнение (1.99) с учетом (1.100) принимает вид:

,

или

.

Очевидно, что выражение не является функцией от , поэтому будем искать функцию  в виде . Тогда, аналогично проведенному выше, имеем

,

откуда окончательно находим

Решая последнее уравнение, находим . Умножив исходное уравнение на , приведем исходное уравнение к уравнению в полных дифференциалах. Его общий интеграл имеет вид:

Отметим, что решение у = -х содержится в общем интеграле при С= ∞.▲

Пример 31. Найти общий интеграл уравнения:

.

▲Это уравнение не является уравнением в полных дифференциалах. Найдем интегрирующий множитель, с помощью которого можно привести исходное уравнение к уравнению в полных дифференциалах.

Пусть  = xy. Тогда согласно (1.99) будем иметь

.

Отсюда находим . Исходное уравнение приводится к уравнению в полных дифференциалах:

Найдем общий интеграл уравнения

▲

Пример 32. Проинтегрировать уравнение:

,

если известно, что для того, чтобы привести исходное уравнение к уравнению в полных дифференциалах необходимо использовать интегрирующий множитель вида: .

▲ Полагаем в условии (1.100) :

Умножая исходное уравнение на этот интегрирующий множитель , мы приведем исходное уравнение к уравнению в полных дифференциалах:

.

Решая это уравнение, найдем общий интеграл исходного уравнения:

.

При умножении исходного уравнения мы предполагали, что у  х², т.к., если у = х², то  обращается в бесконечность. Поэтому у = х² также будет являться решением. Проверим, является ли это решение особым. Для этого составим систему (1.14):

.

Исключая С, установим, что кривой, подозрительной на огибающую будет являться парабола, т.е. у  х². Таким образом, это решение у  х², которое также является решением исходного уравнения, является особым.▲