6. Взаимное расположение прямых и плоскостей. Углы между прямыми.

Пусть две прямые a и b в пространстве, в некоторой аффинной системе координат заданные каноническими уравнениями

a:, (1) b:. (2)

Эти прямые a и b задаются своими направляющими векторами s₁ = (m₁,k₁,l₁), s₂ = (m₂,k₂,l₂) и точками M₁(x₁,y₁,z₁), M₂(x₁,y₁,z₁) которые принадлежат этим прямым. Рас-сотрим вектор .

Рассмотрим матрицу, составленную из координат этих векторов,

.

1. Прямые a и b скрещиваются тогда и только тогда, когда векторы , s₁, s₂ некомпланарны. Последнее равносильно тому, что det A не равен нулю, т.е. rang A = 3.

2. Прямые a и b пересекаются тогда и только тогда, когда векторы , s₁, s₂ компланарны, а векторы s₁ и s₂ неколлинеарны. Последнее равносильно тому, что det A =0, а и вторая и третья строки матрицы A непропорциональны, т.е. rang A = 2, а ранг матрицы, составленной из двух последних строк равен 2.

3. Прямые a и b параллельны тогда и только тогда, когда векторы s₁ и s₂ коллинеарны, а векторы и s₁ неколлинеарны. Последнее равносильно тому, что в матрице А вторая и третья строки пропорциональны, т.е. rang A = 2, а ранг матрицы, составленной из двух последних строк равен 1.

4. Прямые a и b совпадают тогда и только тогда, когда векторы , s₁ и s₂ попарно коллинеарны. Последнее равносильно тому, что все строки матрицы А попарно пропорциональны, т.е. rang A = 1.

Таким образом, доказана следующая теорема.

Теорема 1. Пусть прямые a и b заданы каноническими уравнениями (1) и (2). Тогда справедливы следующие утверждения:

1) a и b скрещиваются тогда и только тогда когда rang A = 3;

2) a и b пересекаются тогда и только тогда, когда rang A = 2, а вторая и третья строки матрицы A непропорциональны;

3) a и b параллельны тогда и только тогда, когда rang A = 2, а вторая и третья строки матрицы A пропорциональны;

4. a и b совпадают тогда и только тогда, когда rang A = 1.

Угол между прямыми в пространстве.

Определение 1. Углом между двумя прямыми называется угол между пересекающимися прямыми, параллельными данным прямым.

Пусть две прямые a и b в пространстве, в некоторой прямоугольной системе заданы каноническими уравнениями (1) и (2) из § 6.

Угол  между прямыми a и b равен углу между их направляющими векторами s₁ = (m₁,k₁,l₁), s₂ = (m₂,k₂,l₂). По определению скалярного произведения векторов

s₁s₂ = s₁ s₂cos .

Отсюда находим формулу косинуса угла между прямыми a и b:

. (3)

Заметим, что прямыми a и b перпендикулярны тогда и только тогда, когда их направляющие векторы s₁ и s₂ ортогональны. По условию ортогональности векторов последнее равносильно тому, что скалярное произведение s₁s₂ = 0. Так как s₁s₂ = m₁m₂+k₁k₂+l₁l₂, то получаем теорему.

Теорема 2. Прямые a и b перпендикулярны тогда и только тогда, когда

n₁n₂ = m₁m₂+k₁k₂+l₁l₂ = 0. (4)

7. Расстояние между двумя прямыми

Определение 1. Расстоянием между двумя прямыми a и b называется кратчайшее расстояние между точками этих прямых

Если прямые a и b пересекаются или совпадают, то расстояние между прямыми равно нулю. Если прямые параллельны или скрещиваются, то кратчайшее расстояние между ними равно длине общего перпендикуляра, проведенного к эти прямым.

Пусть прямые a и b в пространстве, в некоторой прямоугольной системе заданы каноническими уравнениями (1) и (2) из § 6. Эти прямые a и b задаются своими направляющими векторами s₁ = (m₁,k₁,l₁), s₂ = (m₂,k₂,l₂) и точками M₁(x₁,y₁,z₁), M₂(x₁,y₁,z₁) которые принадлежат этим прямым, вектор . Рассмотрим два случая.

Прямые a и b параллельны. Рассмотрим вектор = s₁ и построим параллелограмм M₁ABM₂. Тогда расстояние d между прямыми a и b равно высоте h параллелограмма M₁ABM₂, опущенной на сторону M₁A. По формуле площади S параллелограмма находим S = M₁A h. Далее по определению векторного произведения имеем S =  . Следовательно,

.

Подставляя сюда координаты векторов получаем, что расстояние между параллельными прямыми находится по формуле.

Прямые a и b скрещиваются. Через точки M₁ и M₂ проведем прямые a и b параллельные соответственно прямым a и b. От точки M₁ отложим векторы, = s₁ и = s₂, на этих векторах построим параллелепипед M₁AСBM₂ABС. Расстояние между прямыми a и b равно расстоянию между плоскостями, в которых лежат основания M₁AСB, M₂ABС параллелепипеда, т.е. равно высоте h параллелепипеда. С одной стороны, объем параллелепипеда M₁AСBM₂ABС можно вычислить по формуле: V = Sh, где S - площадь основания M₁AСB. С другой стороны, по свойству смешенного произведения V =. По определению векторного произведения S = . Отсюда получаем, что

.

Подставляя сюда координаты векторов получаем, что расстояние между скрещивающимися прямыми находится по формуле:

.
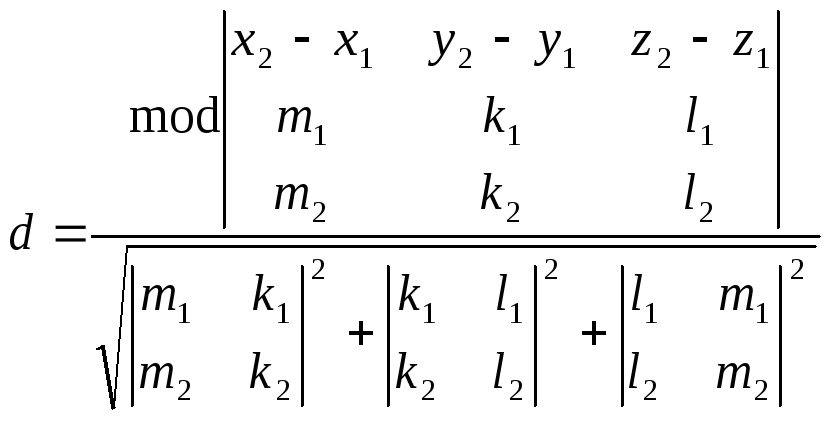