- •7. Вычислить выражения:
- •1. Вычислить:
- •Задание № 4-2.
- •3. Вычислить определители:
- •Задание 6-1.
- •Задание № 73.
- •Задание № 8-1.
- •Задание 9-4.
- •Ответы.
- •Задание 103.
- •Ответы .
- •Задание № 114
- •Ответы .
- •Задание № 125.
- •Ответы.
- •Задание № 13 3.
- •Ответы.
- •Задание № 142.
- •Ответы.
- •Задание № 151.
- •Задание № 16-4.
- •Ответы.
Задание № 1-4.
-
Вычислить выражения:
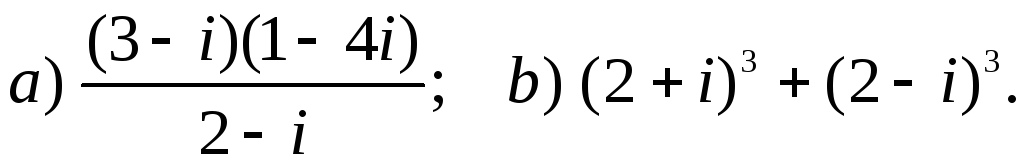
-
Вычислить i 77.
-
Решить систему:
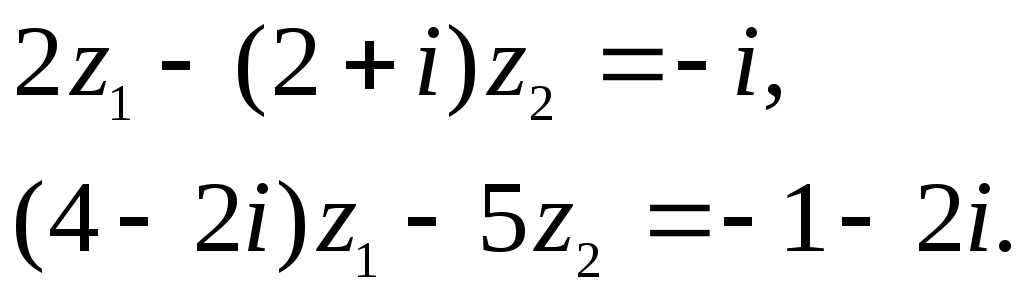
4. Доказать, что два мнимых числа сопряжены тогда и только тогда,
когда их произведение и их сумма - действительные числа.
5. Найти комплексные числа, сопряженные своему квадрату.
6. Найти тригонометрическую форму чисел:
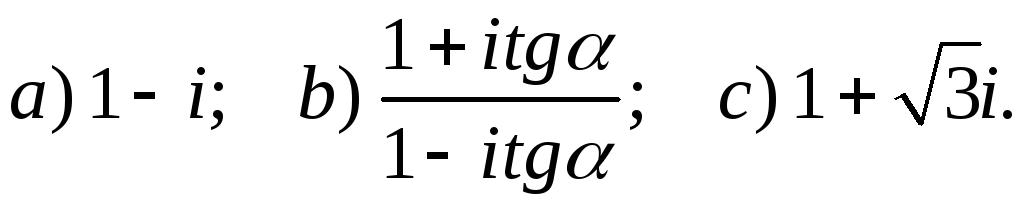
7. Вычислить выражения:
8.
Вычислить

Ответы
1a.
![]() 4. Док-во. 5.
4. Док-во. 5.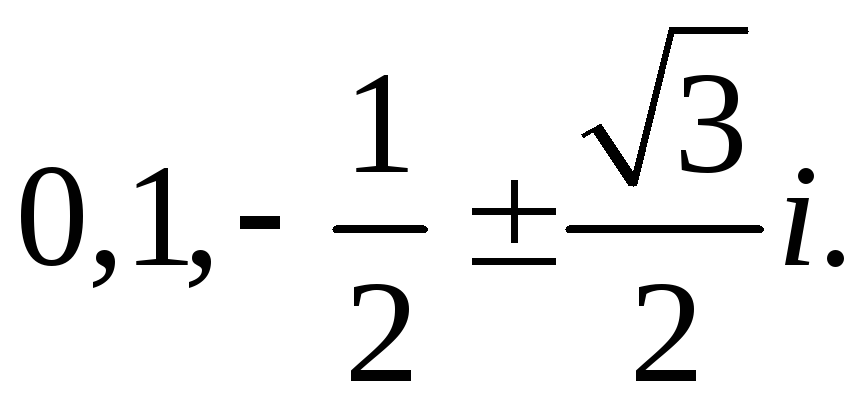
6.
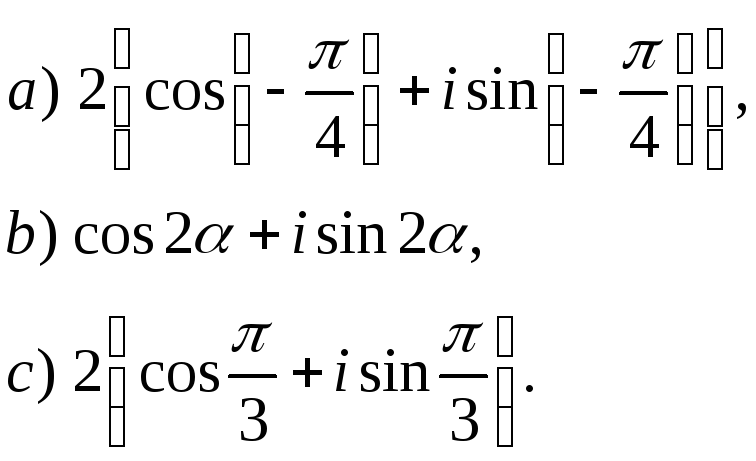
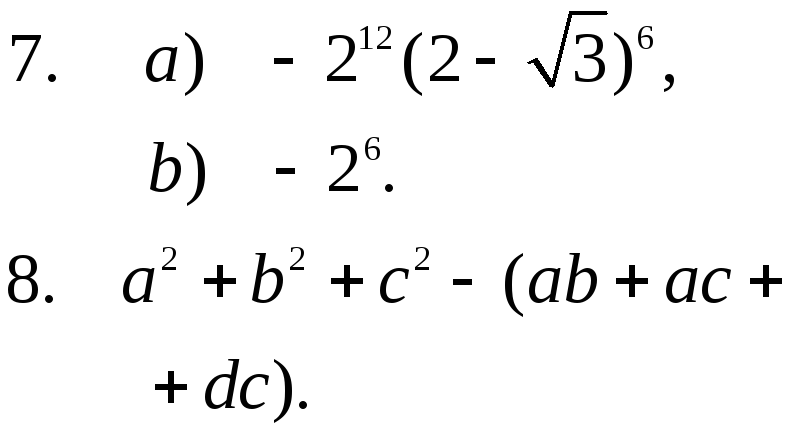
Задание № 2-5.
1. Вычислить:
![]()
2. Определить сумму первообразных корней из 1: а) 24-ой степени,
б) 30-ой степени.
3.
Число
первообразный корень 20-ой степени из
1. Первообразным какой степени из 1
является 6,
если
![]()
4.
При n
Z вычислить
![]()
Ответы.
Вариант 2-5.
1а.
![]() .
2a.
0. 2б. 1.
.
2a.
0. 2б. 1.
1б.
![]() 3. 10.
3. 10.
1в.
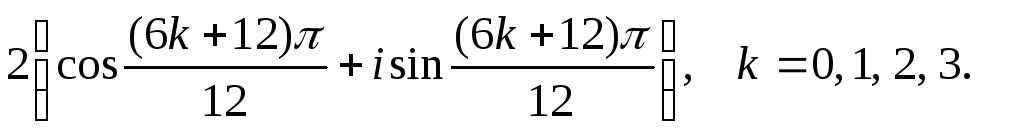
1г.
![]() 4.
4.
![]()
Задание № 3-3.
-
Решить системы уравнений методом Гаусса:
а)
 б)
б)

в)
 г)
г)

д)
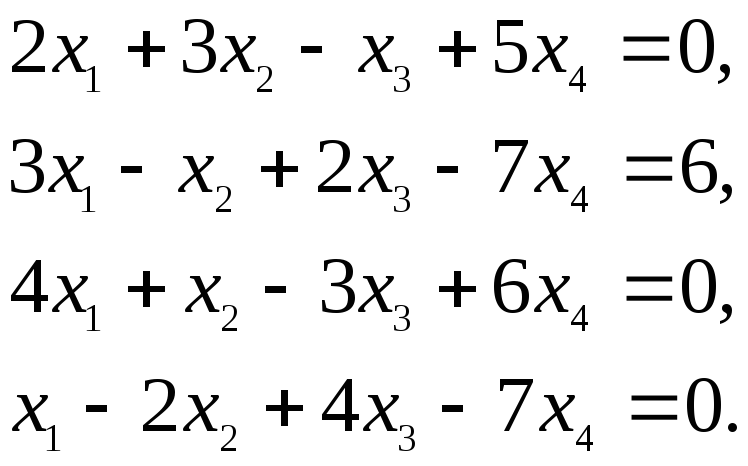 е)
е)
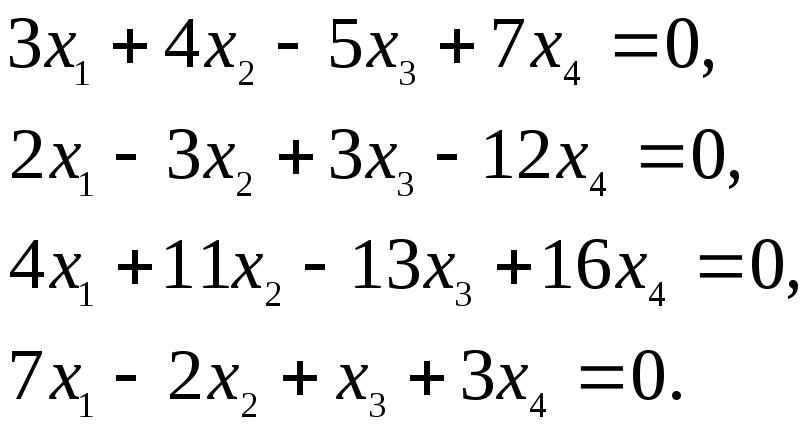
-
Исследовать системы и найти общее решение в зависимости от значений параметров:
а)
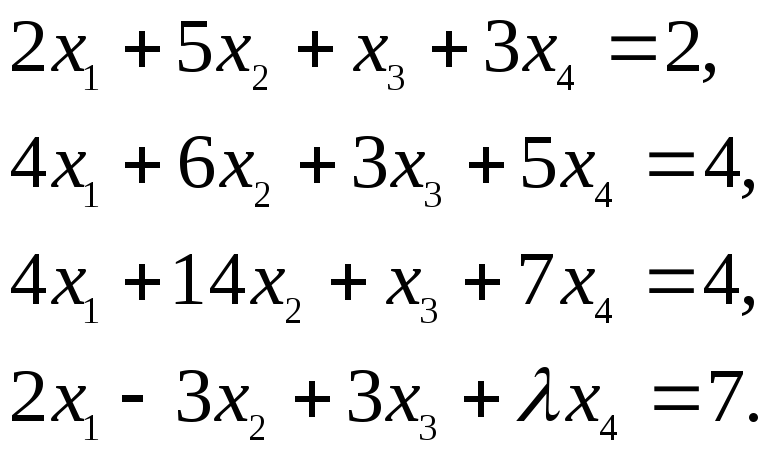 б)
б)
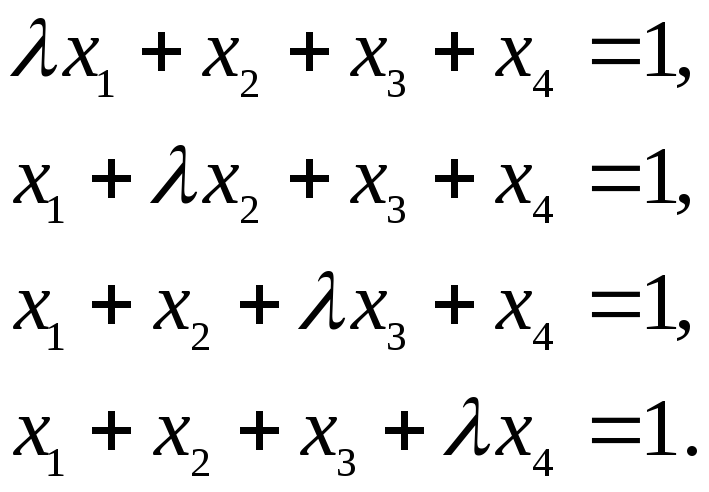
в)
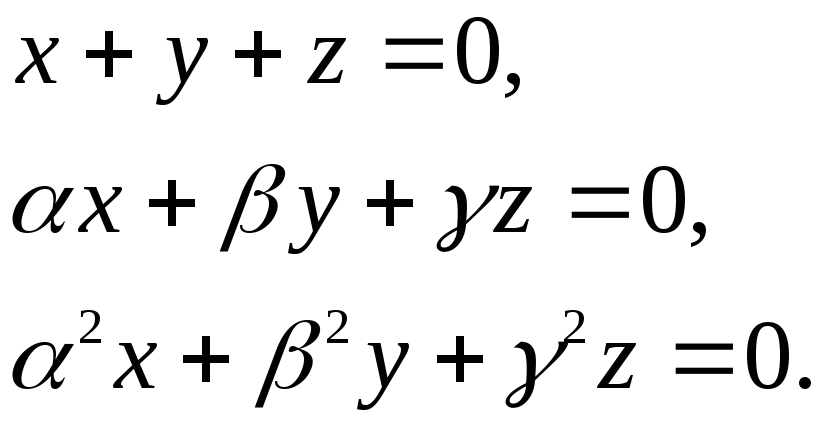 г)
г)
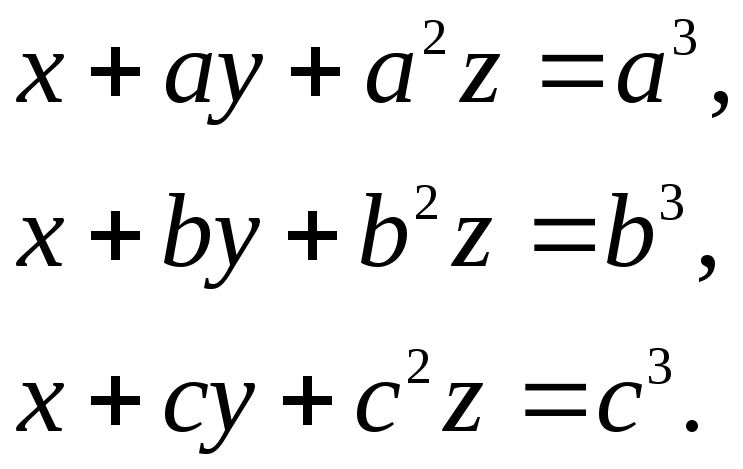
Ответы.
1а. x1 = 2, x2 = 1, x3 = 4, x4 = 3. 1г. x1 = 1, x2 = 2, x3 = 2.
1б. Решений нет. 1д. х1 = x2 = x3 = x4 = 0.
1в. x1 = 1/2(1 i)x4, x2 = x3 = 0. 1e. x1 = 1/17(3x3 13x4 ),
x2 = 1/17(19x3 20x4 ).
2a. = 1: система несовместна,
1:
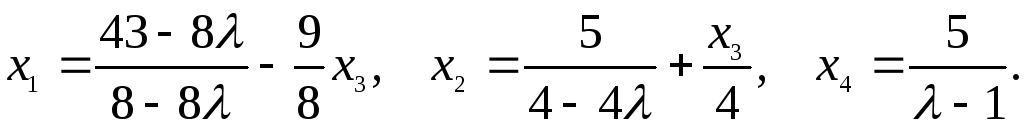
2б. 1, 3: x1 = x2 = x3 = x4 =1/ + 3, = 1: x1 =1 x2 x3 x4 ,
= 3: система несовместна.
2в. ![]()
попарно различны
ненулевых решений нет, если есть равные
пары, решение зависит от одного параметра,
при
попарно различны
ненулевых решений нет, если есть равные
пары, решение зависит от одного параметра,
при ![]()
от двух
от двух
параметров.
2г. Если а, b, c различны, x = abc, y = (ab + bc + ac), z = a + b + c,
если среди a, b, c есть пара равных, решение зависит от одного параметра, если a = b = c, решение зависит от двух параметров.
Задание № 4-2.
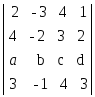
1. Вычислить определители:
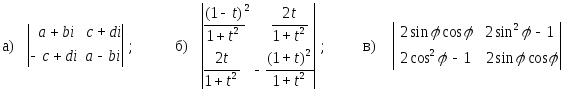 ;
;
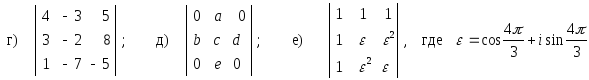
2. Пользуясь
теоремой Крамера, решить системы:![]()

3. Перемножить перестановки в указанном и обратном порядке.

4. Найти обратную
перестановку:
 .
.
5. Определить число инверсий в последовательностях:
а) 2, 3, 5, 4, 1; б) 6, 3, 1, 2, 5, 4; в) 1, 3, 5, 7, ... , 2n-1, 2, 4, 6, 8, ... , 2n.
6. Определить четность перестановок:

7. С какими знаками входят данные произведения в определители соответствующих порядков ?
![]()
8. Выписать
все слагаемые, входящие в состав
определителя 4-го порядка со знаком
””
и содержащие множитель
![]() .
.
9. С каким знаком входит в определитель порядка n произведение элементов побочной диагонали ?
Ответы
1а.
a2 +
b2 +
c2 +
d2.
1б.
1.
1в.
1. 1г.
100. 1д.
0. 1е.
3i![]() .
2a. х1 =
3, x
.
2a. х1 =
3, x![]() =
1.
2б.
x = a,
y = b, z = c. 2в.
x1 =
3, x2 =
x = x3 =
1.
=
1.
2б.
x = a,
y = b, z = c. 2в.
x1 =
3, x2 =
x = x3 =
1.
3а.
![]() 3б.
3б.
![]() 3в.
3в.
![]()
4а.
![]() 4б.
4б.
![]() 5а.
5. 5б.
8. 5в.
5а.
5. 5б.
8. 5в.
![]() 6а.
3().
6б.
11().
6в.
неч.
7а.
().
7б.
(+). 7в.
(+).
6а.
3().
6б.
11().
6в.
неч.
7а.
().
7б.
(+). 7в.
(+).
8.
a11 a23 a32 a44,
a12 a23 a34 a41,
а14
a23 a31 a42.
9.
![]()
Задание 5-1.
1. Как изменится определитель порядка n, если:
а) у всех его элементов изменить знак на противоположный ?
б) каждый его
элемент
![]() умножить на
умножить на
![]() ?
?
в) каждый его элемент заменить элементом, симметричным относительно
побочной диагонали ?
2. Разлагая по третьей строке, вычислить определитель: