
- •Министерство образования и науки Российской Федерации
- •Введение
- •1. Выводимость
- •Варианты заданий.
- •2. Исчисление высказываний
- •Варианты заданий.
- •3. Отношение эквивалентности
- •Варианты заданий.
- •Метатеория исчисления высказываний
- •Варианты заданий.
- •Библиографический список
- •Исчисление высказываний
- •394000 Воронеж, пр. Революции, 19
Варианты заданий.
-
Какие из следующих выражений являются формулами исчисления высказываний:
-
 ;
; -
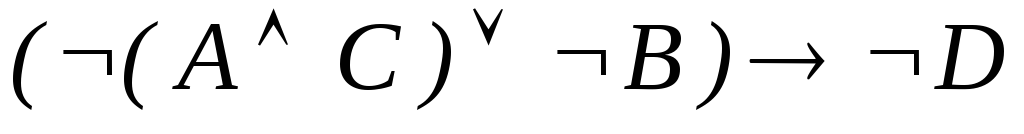 ;
; -
 ;
; -
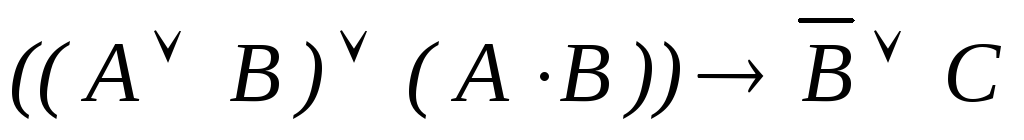 ;
; -
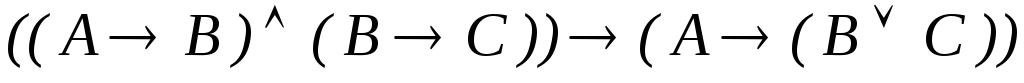 .
.
-
-
Выписать все подформулы формул:
-
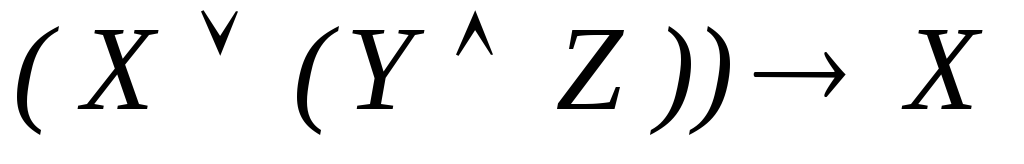 ;
; -
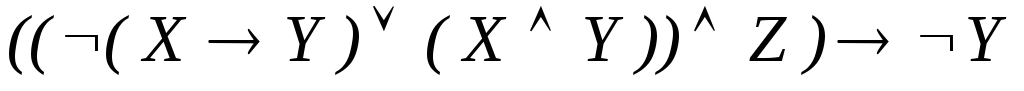 ;
; -
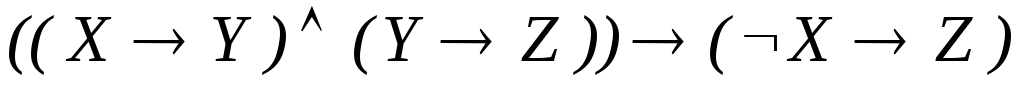 ;
; -
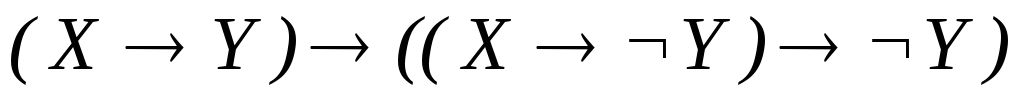 .
.
-
Применяя правила подстановки и заключения, доказать, что следующие формулы являются теоремами исчисления высказываний (3 – 10).
Применяя правила подстановки и заключения, построить вывод формул из данной системы посылок (11 - 15).
Являются ли выводами в исчислении высказываний следующие последовательности формул (16 – 18).
![]()
![]()
![]()
B
Применяя производные правила вывода, показать, что доказуемы формулы (19 – 36).
-
U B, P Q ú- (U P) (B Q)
-
U B, P Q ú- (U P) (B Q)
-
U B, P Q ú- (B P) (U Q)
-
 ú-
ú-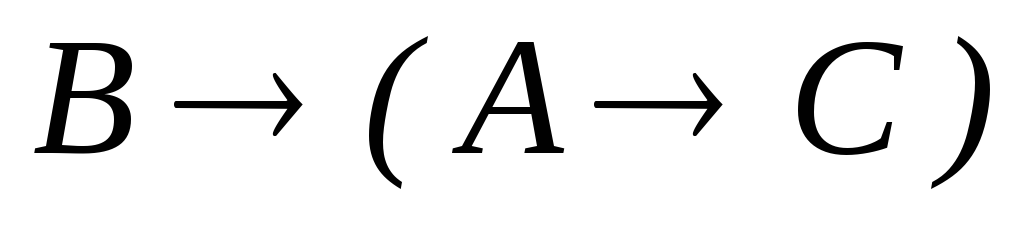
-
 ú-
ú-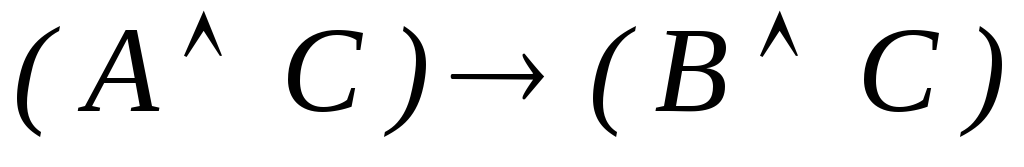
-
(P Q) ((Q R) (P R))
-
(P Q) ((R P) (R Q))
-
Q ® R (P Ú Q) ®(P Ú R)
-
(P ® Q) Ú (Q ® P),
-
P ® (Q® (P Q))
-
(P ® Q) Ú (P ® Q)
-
(P ® Q)®((P ® (Q ® R)) ® (P ® R)))
-
((P ® R)® ((Q ® R) ® ((P Q) ® R)))
-
((P® Q) ® ((P ® Q) ® P))
-
(( Q ® P) ® (( Q ® P) ® Q))
-
Q ((P Q) (Q P)
-
Q (P Q) (P Q)
-
Q (P R Q Q)
Применяя производные правила вывода, построить вывод формул (37 – 43).
-
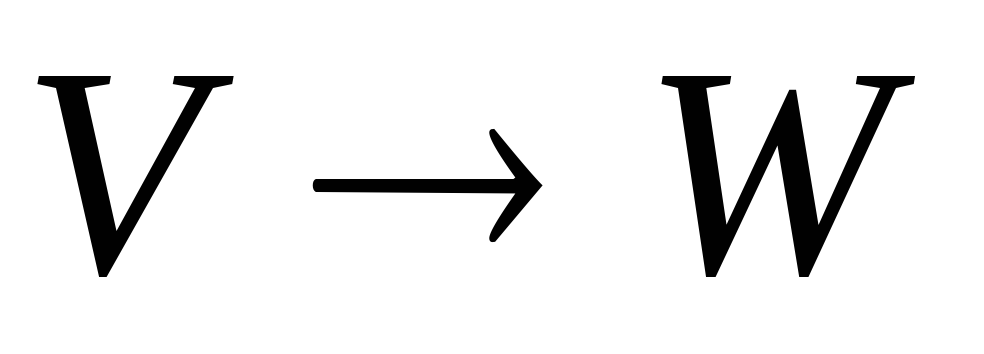
 ,
,

-

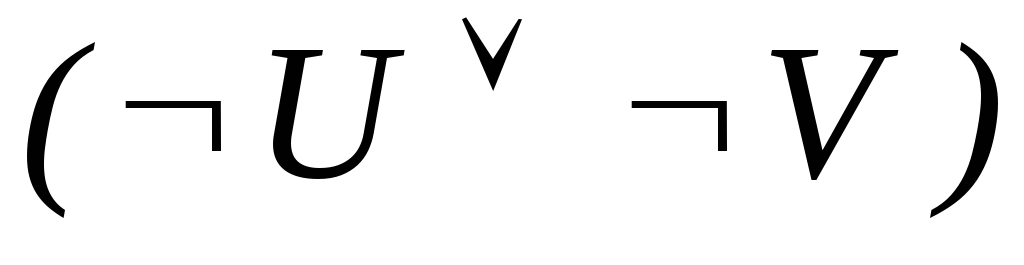
-
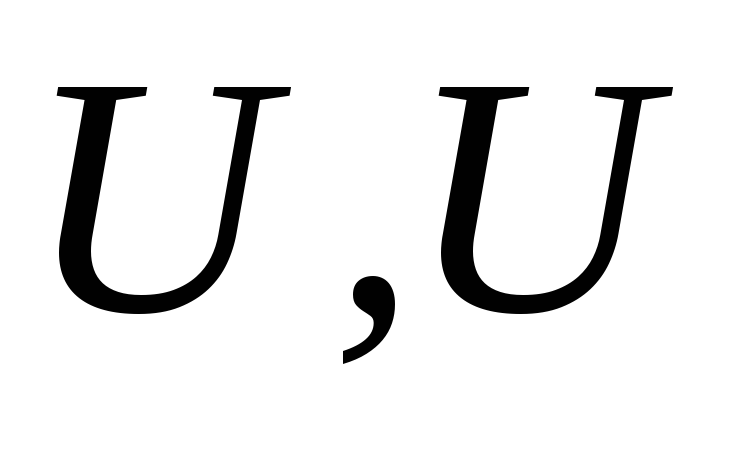

-

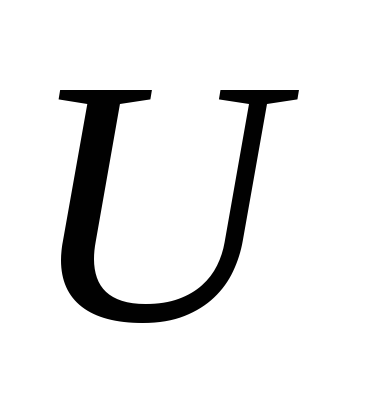
-
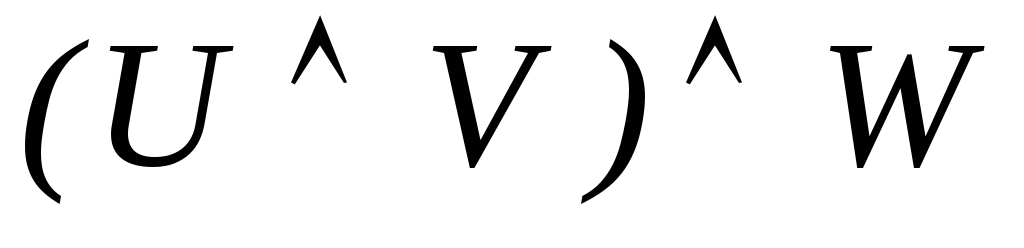

-
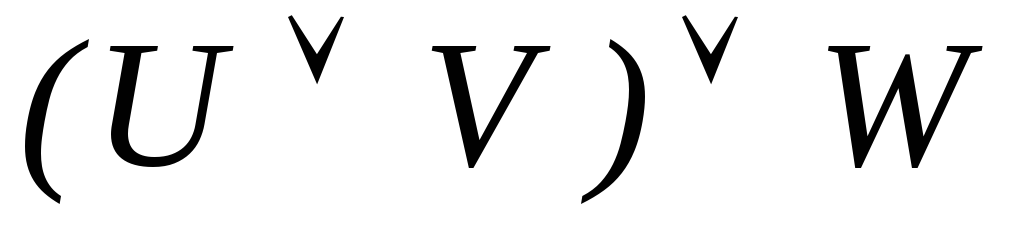
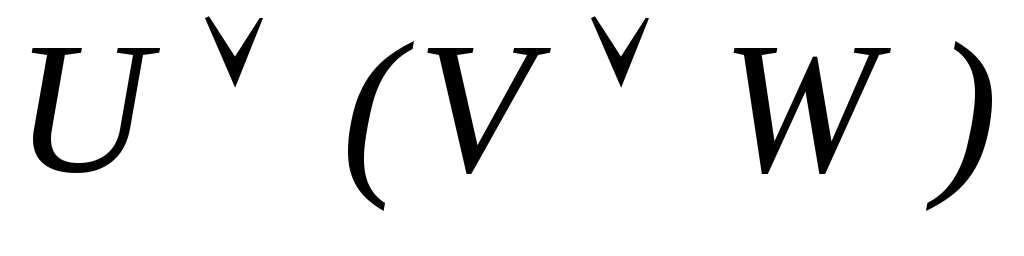
-

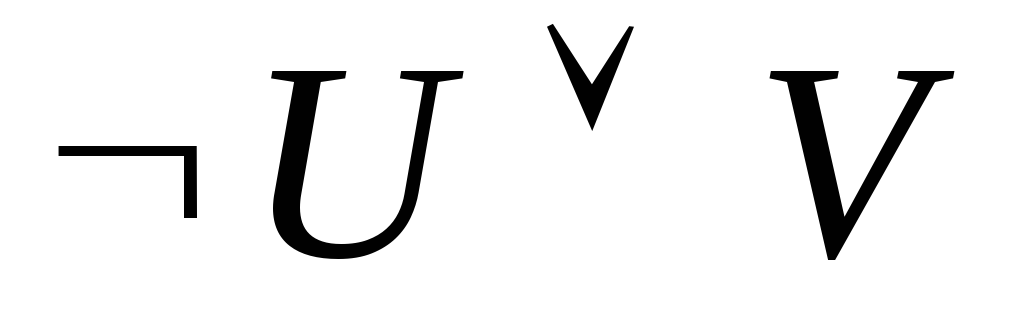
Применяя производные правила вывода, построить вывод формул. Проверить, справедлива ли выводимость в обратную сторону, если да, то построить вывод (44 – 59).
-
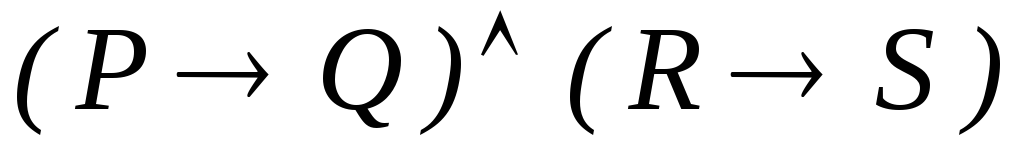
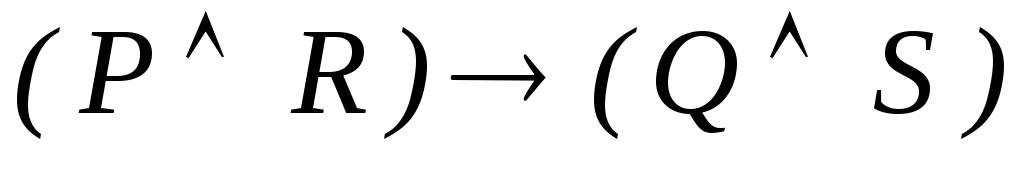
-
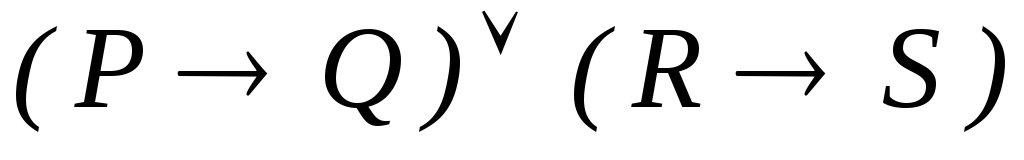

-

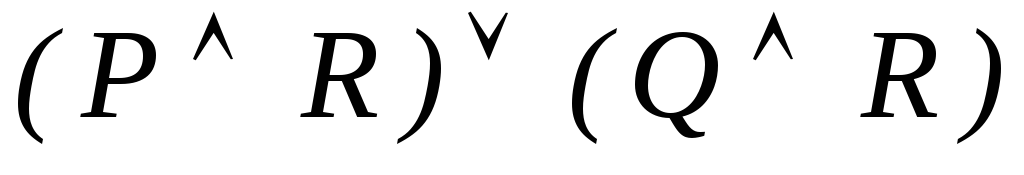
-
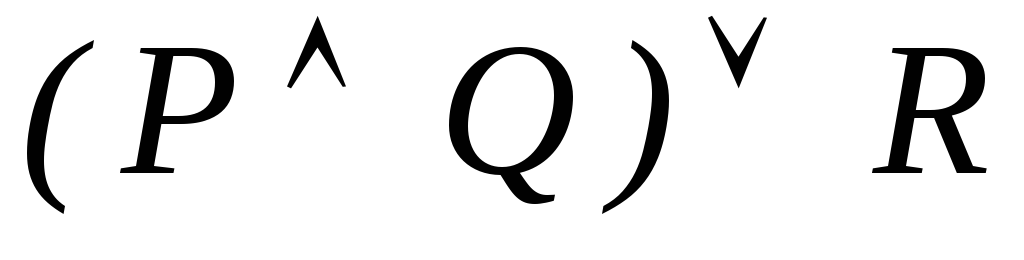
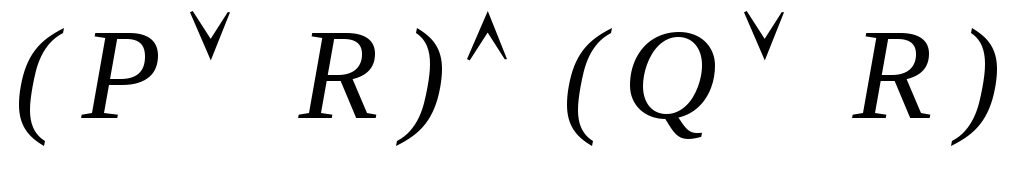
-
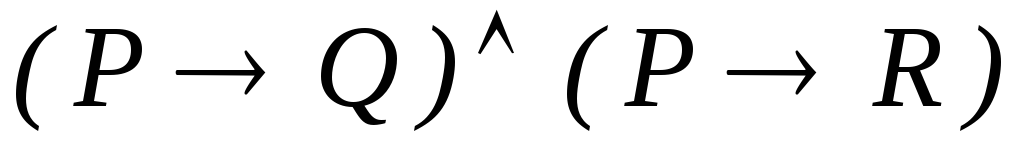
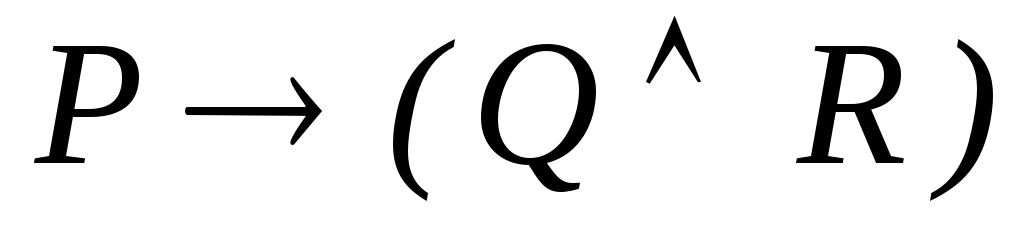
-
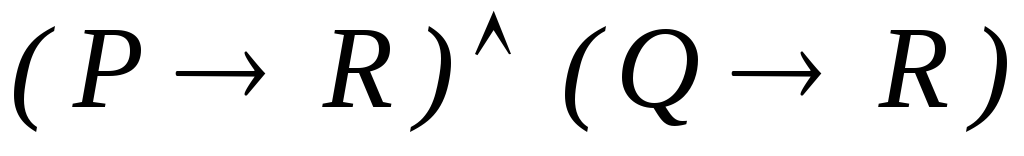
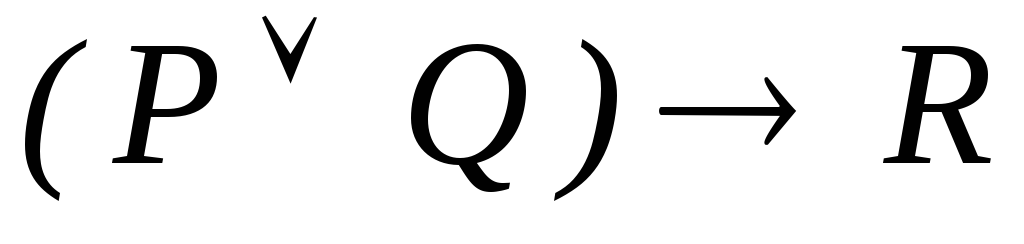
-
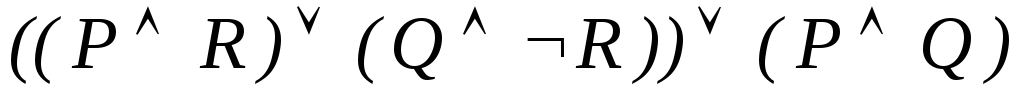
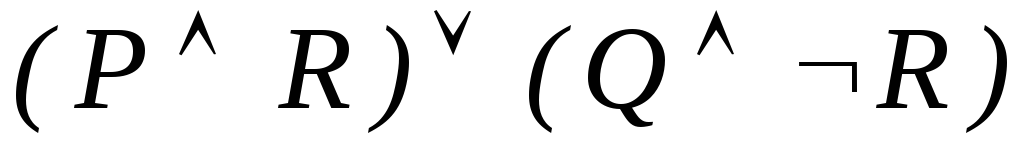
-
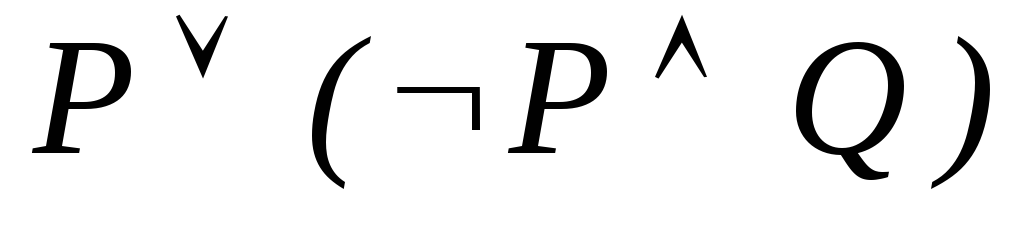

-
A (C P) (A C) P
-
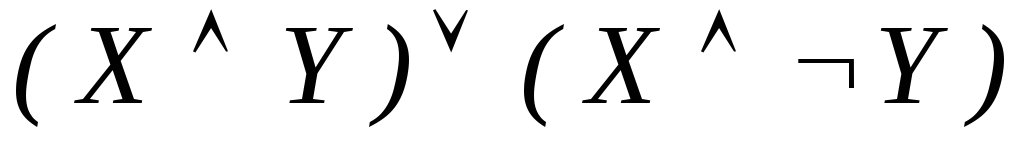
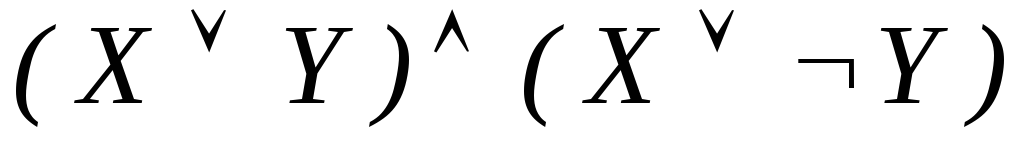
-
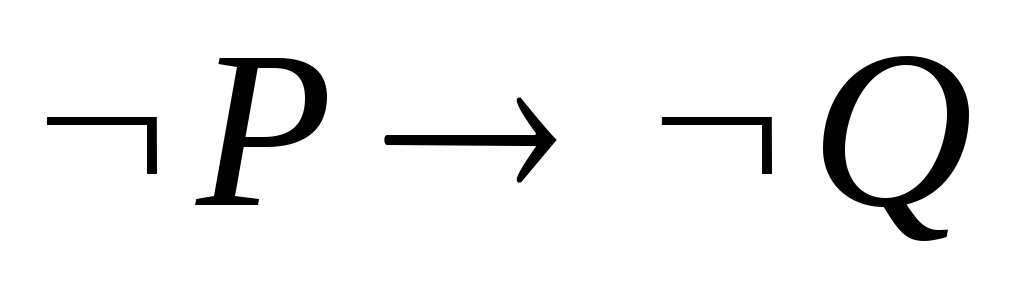
(
(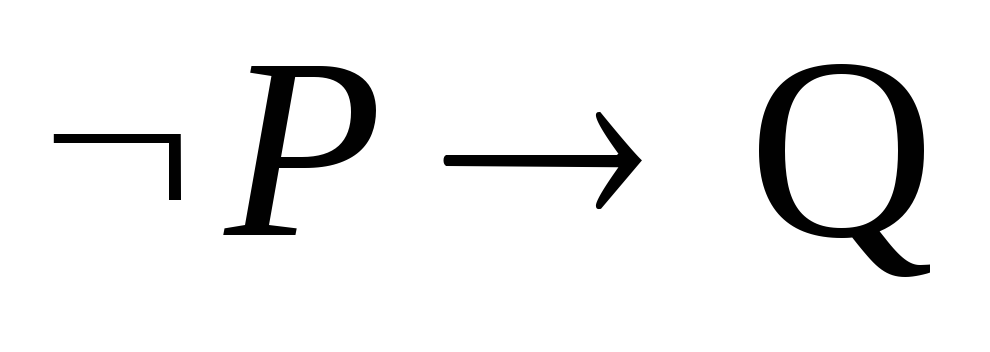 )
P
)
P -
P Q (P
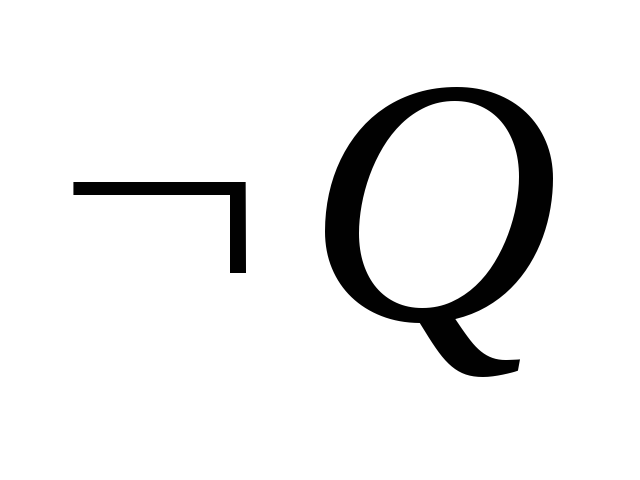 )
)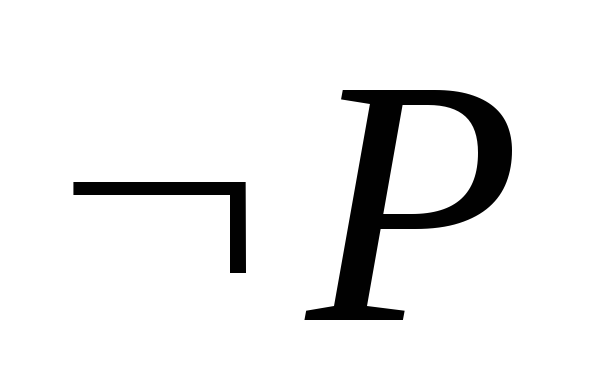
-
P R Q ú- ((P ® R) ® (
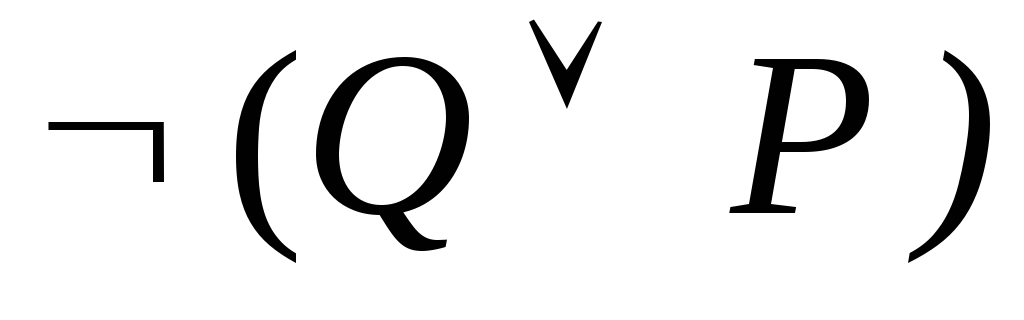 ®
R
®
R -
(P Q) (P (Q R)) ú- ( P R)
-
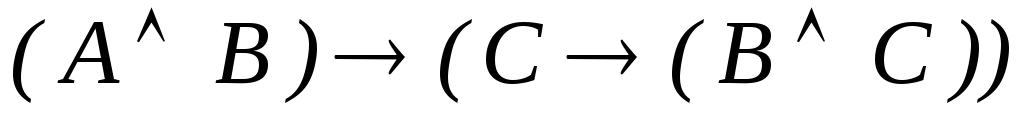 ú-
ú-
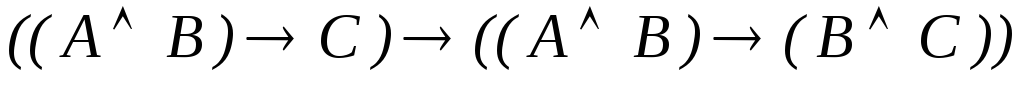
-
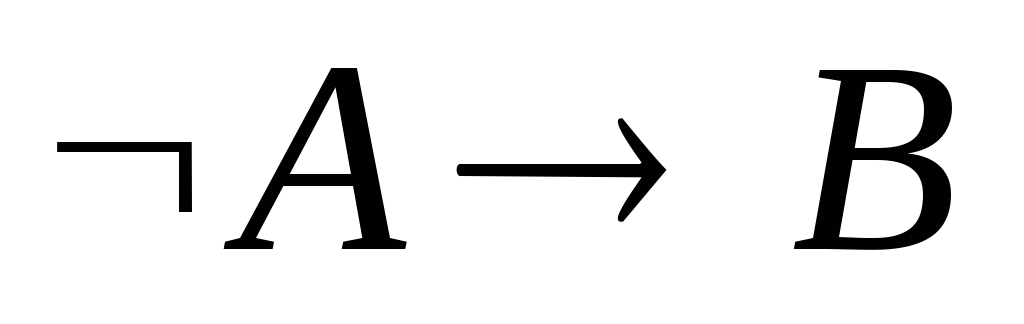 ú-
ú-
-
Пусть А – формула, В – подформула формулы А, А1 - результат замены некоторого вхождения В в А на формулу В1. Доказать (В ~ В1) ú- (А ~ А1). (Теорема о замене)
-
Доказать, что если выводима формула U1, …, Un ú- B, то формула (U1 … Un B) тождественно истина.
-
Найти такие формулы
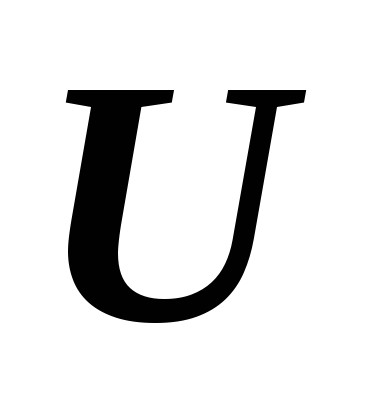 и
и
 ,
что из доказуемости
,
что из доказуемости
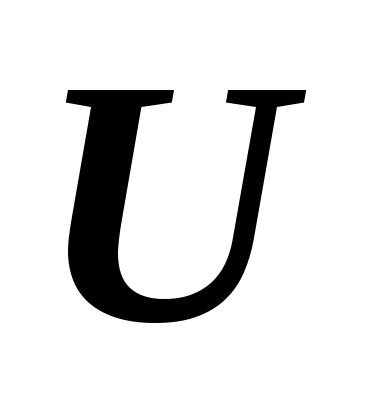 в исчислении высказываний следует
доказуемость
в исчислении высказываний следует
доказуемость
 ,
но неверно, что
,
но неверно, что
 ú-
ú- .
.
3. Отношение эквивалентности
Определим эквивалентность формул в исчислении высказываний.
Определение
1.
Формулы U
и
B
называются эквивалентными, что
обозначается ![]() ,
если
,
если
![]() (1)
(1)
Рассмотрим некоторые простые свойства отношения эквивалентности.
-
Рефлексивность:
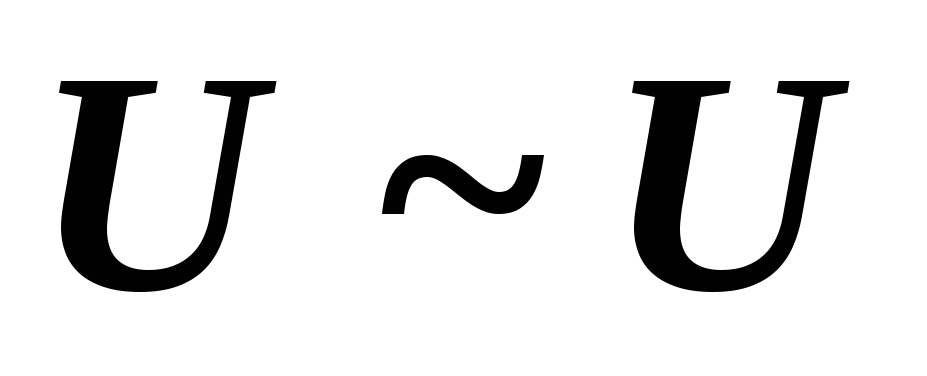 .
. -
Симметричность: если
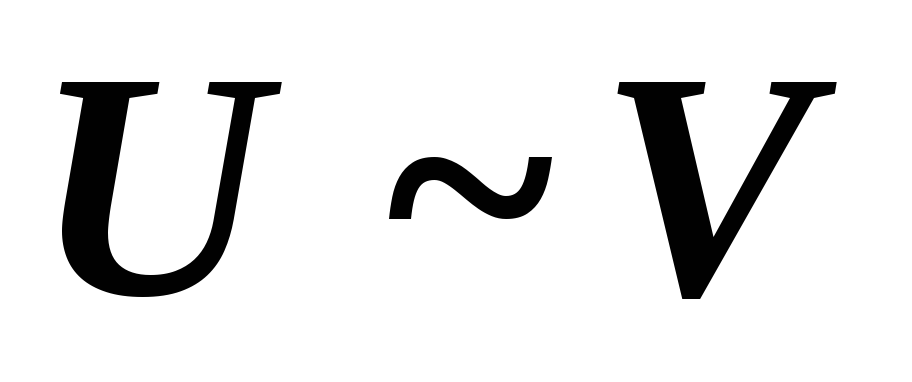 ,
то
,
то  .
. -
Транзитивность: если
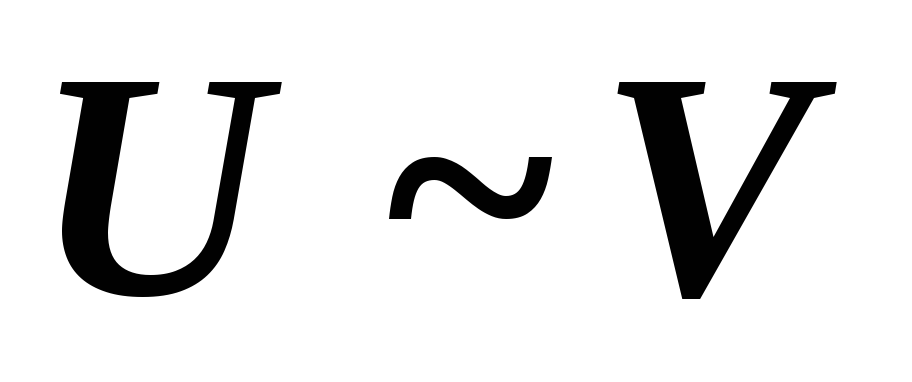 и
и
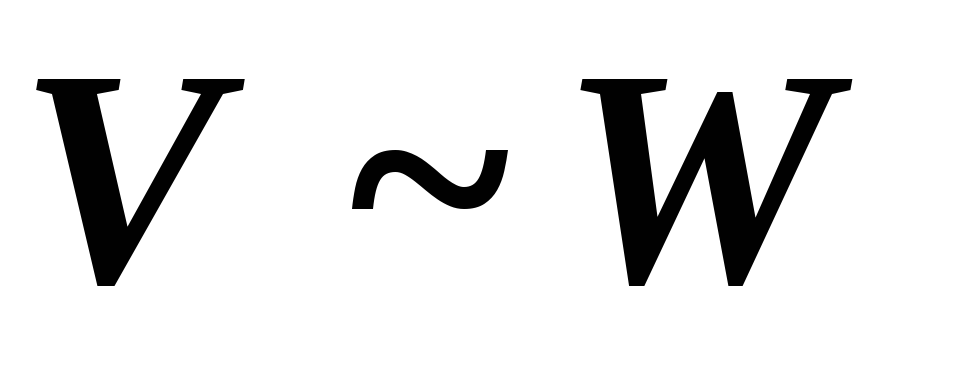 ,
то
,
то 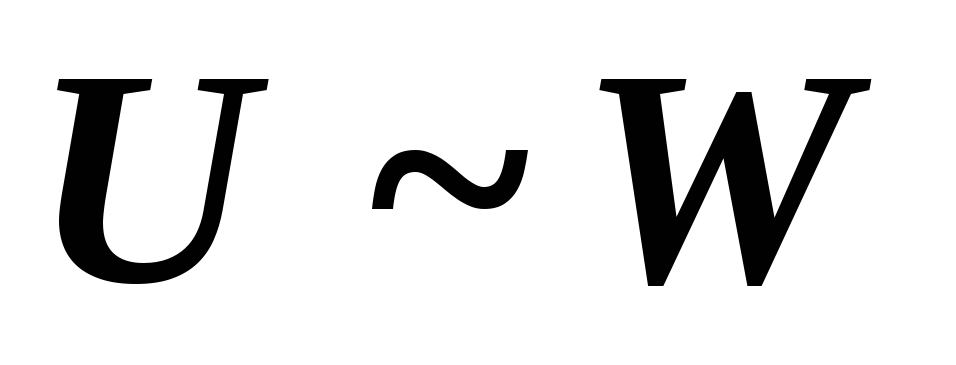 .
.
Задание 1. Доказать свойство симметричности отношения эквивалентности.
Решение.
-
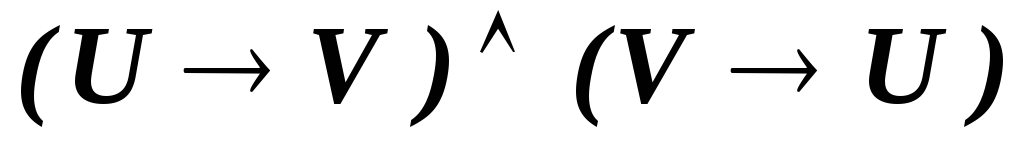
-
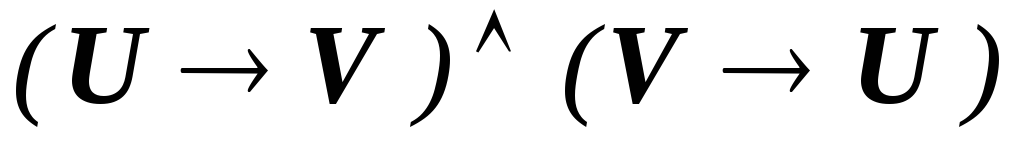
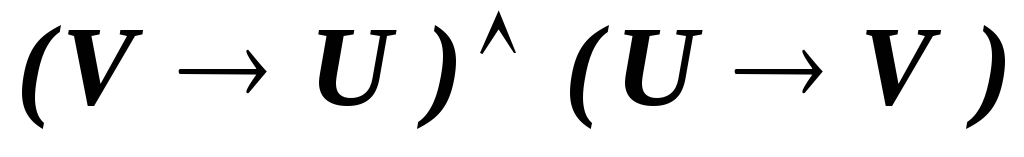
-
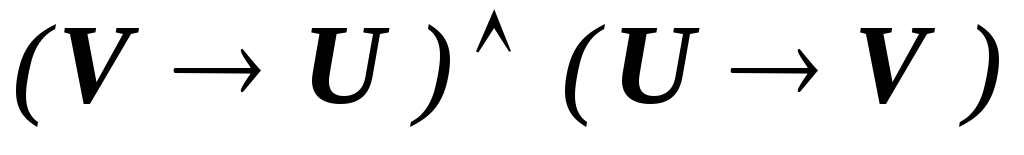
Из свойств отношения эквивалентности следует, что множество формул исчисления высказываний разбивается на непересекающиеся классы эквивалентных друг другу формул (классы эквивалентности). Следовательно, все теоремы исчисления высказываний образуют один класс эквивалентных формул.
В исчислении высказываний имеют место следующие эквивалентности, которые соответствуют аналогичным свойствам отношения эквивалентности алгебры высказываний.
-
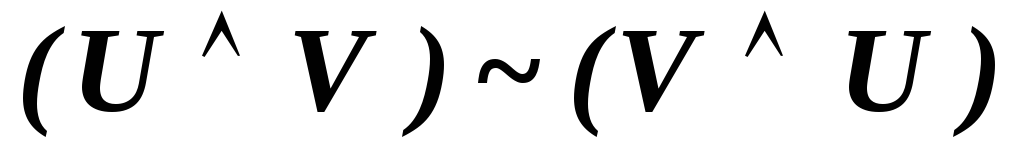 .
. -

-
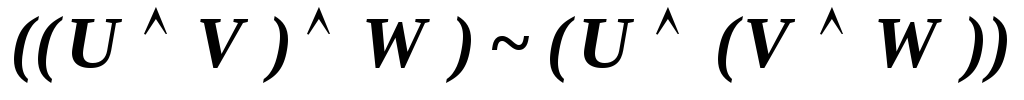
-
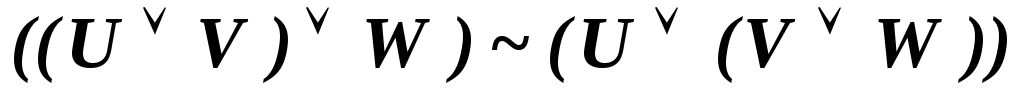
-
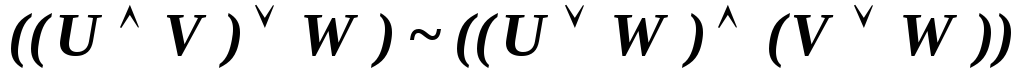
-
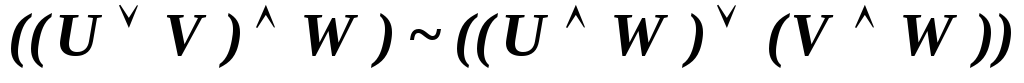
-

-
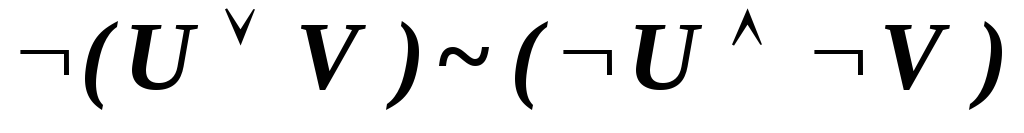
-
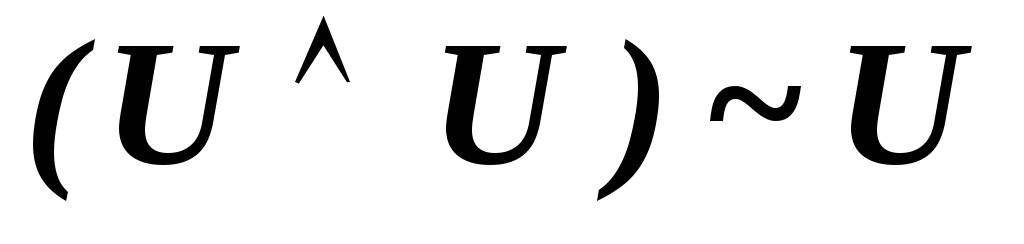
-
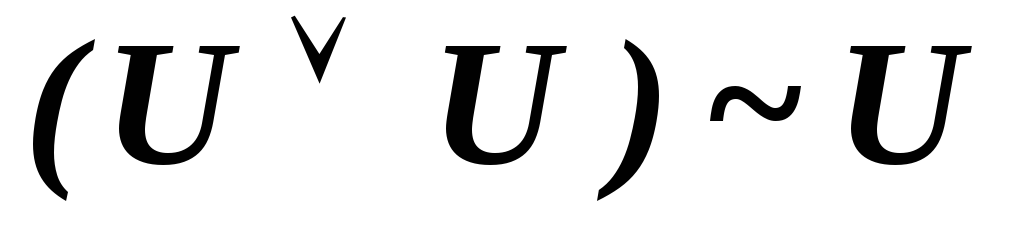
-
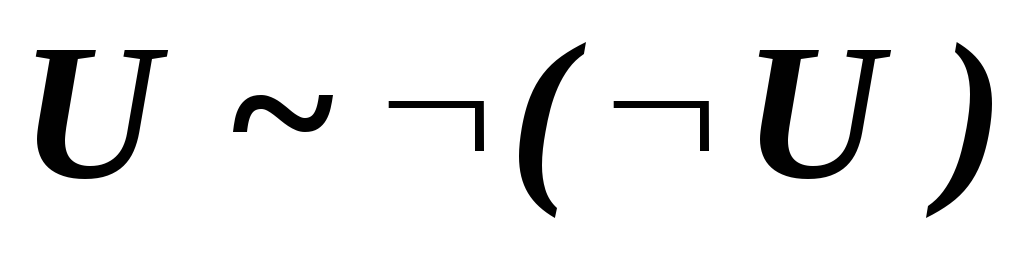
-
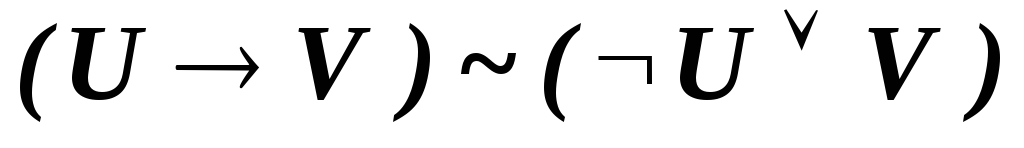
Для того чтобы
доказать эквивалентность ![]() в исчислении высказываний достаточно
построить выводы
в исчислении высказываний достаточно
построить выводы
![]()
![]() и
и
![]()
![]() .
Покажем, что если
.
Покажем, что если
![]()
![]() и
и
![]()
![]() ,
то
,
то ![]() .
.
|
1.
|
по условию |
|
2.
|
по условию |
|
3. |
5 (1) |
|
4. |
5 (2) |
|
5.
|
7 |
|
6. |
4 (3, 4, 5) |
Последняя
формула, в силу определения, означает
![]() .
.
Теорема
эквивалентности. Если
![]() и
и
![]() - формулы, полученные заменой некоторых
(одних и тех же) вхождений какой-либо
высказывательной переменной в формуле
U
соответственно формулами
- формулы, полученные заменой некоторых
(одних и тех же) вхождений какой-либо
высказывательной переменной в формуле
U
соответственно формулами
![]() и
и
![]() ,
то
,
то
![]()
![]() .
.
Следствие.
Если
![]() есть некоторая подформула формулы U
и
есть некоторая подформула формулы U
и
![]() эквивалентна формуле
эквивалентна формуле
![]() ,
то формула, полученная заменой
,
то формула, полученная заменой
![]() в формуле U
на
в формуле U
на
![]() ,
эквивалентна U.
Иными словами, если
,
эквивалентна U.
Иными словами, если
![]() ,
то
,
то
![]() .
.
Свойства
2, 4, 10 и теорема эквивалентности позволяют
формулу, составленную из высказывательных
переменных
![]() лишь с помощью операции дизъюнкции,
преобразовать к виду
лишь с помощью операции дизъюнкции,
преобразовать к виду
![]() .
.
Аналогично
формула, составленная из
![]() с помощью операции конъюнкции эквивалентна
формуле
с помощью операции конъюнкции эквивалентна
формуле
![]() .
.
Это позволяет дать определение понятиям нормальных форм исчисления высказываний, которые совпадают с соответствующими определениями алгебры высказываний.
Теорема
3.1. Для каждой
формулы
![]() исчисления высказываний существуют
эквивалентные ей дизъюнктивная и
конъюнктивная нормальные формы.
исчисления высказываний существуют
эквивалентные ей дизъюнктивная и
конъюнктивная нормальные формы.
