1.2. Матриці і їх властивості

. Матрицею розміру називається прямокутна таблиця, що складається з елементів , та містить рядків і стовпців. Кожну таку таблицю беруть в круглі дужки або подвійні вертикальні риски.

Наприклад

, або .

В скороченому запису матриця позначається

; або ; ; .

Елементи називаються елементами матриці: індекс означає |значить|номер рядка, а номер стовпця, на перетині|пересіченні| яких стоїть елемент.

Матриця, в якій число рядків дорівнює числу стовпців, називається квадратною. Кількість рядків (або стовпців) квадратної матриці називають її порядком.

Матриця, в якій всього один рядок, називається матрицею-рядком, а матриця, у|біля| якої всього один стовпець, – матрицею-стовпцем.

. Множення матриць.

1. Операція множення матриці на матрицю вводиться тільки для узгоджених матриць. Матриця називається узгодженою з матрицею , якщо кількість стовпців матриці дорівнює кількості рядків матриці .

Добутком двох матриць і , заданих у визначеному порядку ( – перша, друга) називається матриця , кожен елемент якої дорівнює сумі добутків елементів го рядка матриці на

відповідні елементи го| стовпця матриці :

де ; .

Приклад 1.4. Обчислити добуток матриць, якщо

; .

Розв’язок. ,

де ; ; .

Таким чином, остаточно маємо:

.

. Транспонування матриці

Транспонувати квадратну матрицю означає поміняти місцями рядки і стовпці матриці із збереженням їх нумерації. Транспонована матриця позначається .

Наприклад, , .

. Обернена матриця

Оберненою матрицею по відношенню до заданої квадратної матриці називається така квадратна матриця, що позначається , яка задовольняє рівностям

и .

Для того, щоб квадратна матриця мала обернену матрицю , необхідно, щоб|аби| матриця була не виродженою, тобто, щоб|цебто| її визначник . Тоді обернена матриця визначається за формулою:

. (1.4)

Таким чином, для знаходження оберненої матриці , необхідно спочатку обчислити|обчисляти| визначник матриці і переконається, що матриця не вироджена , потім записати транспоновану матрицю .

1.3. Розв’язок систем лінійних рівнянь

Розглянемо|розглядуватимемо| три способи розв’язку систем лінійних рівнянь: за формулами Крамера, матричним способом, методом Гауса.

Нехай|нехай| дана система лінійних рівнянь

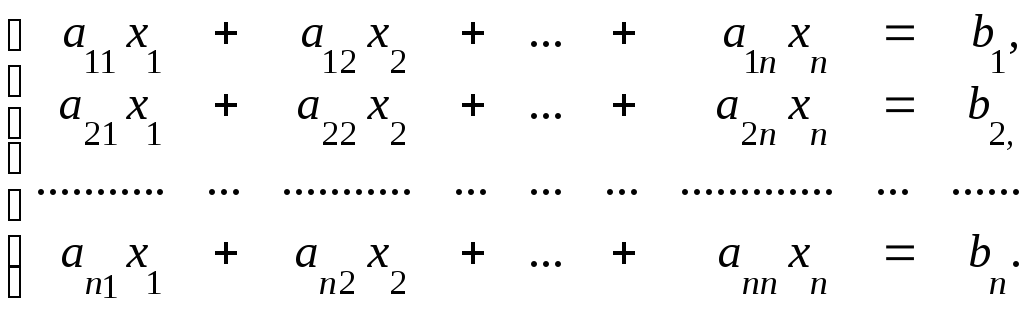(1.5)

. При розв’язку системи (1.5) за формулами Крамера, невідомі знаходяться із співвідношень:

, , …, , (1.6)

де визначник системи, складений із|із| коефіцієнтів при невідомих, , , …, визначники невідомих, які отримують із|із| визначника заміною його першого, другого …, го| стовпця відповідно стовпцем вільних членів.

. Розв’язок системи лінійних рівнянь (1.5) матричним способом.

Якщо ввести|запроваджувати| матричні позначення

, , ,

то систему можна записати матричним рівнянням

. (1.7)

Помножимо обидві частини|частки| цього рівняння на обернену матрицю

. (1.8)

Тобто|цебто|, щоб|аби| розв’язати|рішати| систему (1.5), необхідно знайти матрицю , обернену до матриці системи і помножити її на матрицю вільних членів (див. розділ 1.2).

Формулу (1.8) називають матричним записом розв’язку системи рівнянь (1.5) або розв’язком матричного рівняння (1.7).

. Розв’язок систем лінійних рівнянь методом Гауса.

Одним з найбільш простих методів розв’язку систем лінійних рівнянь є метод безпосереднього виключення|винятку| невідомих, або метод Гауса. Цей метод базується на елементарних перетвореннях системи рівнянь, або простіше, розширеної матриці.

Розширеною матрицею системи лінійних рівнянь (1.5) називають матрицю коефіцієнтів системи (1.5) з|із| доданим|добавляти| ще одним стовпцем вільних членів, який відділяється|відокремлюється| рискою:

. (1.9)

Під елементарними перетвореннями розширеної матриці мають на увазі|слідуючі|:

1. перестановку будь-яких двох рядків матриці;

2) множення якого-небудь рядка матриці на будь-яке, відмінне від нуля|нуль-індикатора| число;

3) додавання до будь-якого рядка матриці відповідних членів іншого рядка, помножених на одне і те ж число.

Ідея методу Гауса полягає в тому, щоб за допомогою елементарних перетворень привести розширену матрицю до рівносильної матриці трикутного (або діагонального) вигляду.

Потім по отриманій|одержувати| трикутній розширеній матриці відновлюється рівносильна система лінійних рівнянь, з|із| якої послідовно знаходяться|перебувають| всі невідомі.