1.4.3. Волна разрежения в жидкости и пузырьковой жидкости

Волна разрежения в жидкости. Рассмотрим решение системы уравнений гидродинамики (4.1.1), описывающее волну разрежения в жидкости, с уравнением состояния

(4.3.1)

Пусть жидкость движется влево, а волна – вправо. Тогда из (4.1.6), (4.1.7) и (4.3.1) следует, что

или . (4.3.2)

Поскольку скорость звука принята постоянной, то ограничение на скорость жидкости в волне разрежения может быть найдено из условия неотрицательности давления жидкости

. (4.3.3)

Оно имеет вид

. (4.3.4)

Волна разрежения в пузырьковой жидкости. Рассмотрим волну разрежения в пузырьковой жидкости с уравнением состояния:

. (4.3.5)

Скорость звука в пузырьковой жидкости определяется выражением

. (4.3.6)

Тогда при подстановке c в интеграл (4.1.8) получим:

. (4.3.7)

Здесь для определённости выбрано течение среды влево. Из (4.3.7) выразим давление

. (4.3.8)

Из уравнения состояния следует

. (4.3.9)

Скорость звука с учетом (4.3.9) примет вид

. (4.3.10)

Подставляя из (4.3.8) в (4.3.10), найдем

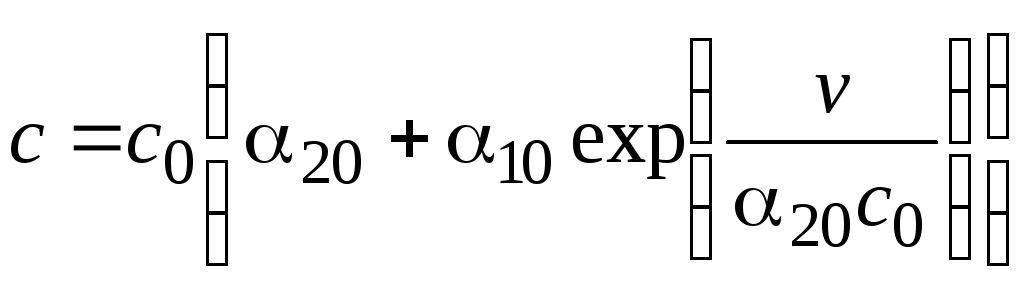. (4.3.11)

Учитывая (4.1.7), получим трансцендентное уравнение для скорости смеси

. (4.3.12)

Решая его, найдем . Скорость звука легко находится по скорости среды:

. (4.3.13)

По формуле (4.3.8) находится давление. Наконец, плотность можно найти из уравнения состояния или по следующей формуле

. (4.3.14)

Таким образом, все параметры пузырьковой жидкости найдены.

Заметим, что распределение скорости пузырьковой жидкости в волне разрежения нелинейное, в то время как в газе и жидкости оно было линейным. Но ограничение на скорость среды есть в газе и жидкости, как было показано выше, а в пузырьковой жидкости, в рамках рассмотренной модели, аналогичных ограничений нет. Действительно, из (4.3.11) следует, что при любых значениях скорости , а из (4.3.5) следует, что всегда.

1.5. Распад произвольного разрыва

Рассмотрим задачи о распаде произвольного разрыва в газе, жидкости и пузырьковой жидкости.

1.5.1. Распад произвольного разрыва в покоящемся газе

Разрывы могут быть устойчивыми и неустойчивыми. К разрывам первого типа относятся, например, разрывы на контакте различных сред (жидкость - газ, жидкость - твердое тело и т.д.) – контактные разрывы и ударные волны. Неустойчивые разрывы распадаются. Мы рассмотрим три наиболее интересных случая распада неустойчивого разрыва – распад произвольного разрыва, столкновение двух масс газа и их разлет. В этом параграфе будет рассмотрен вопрос о распаде произвольного разрыва.

Рис. 1.15.

Рассмотрим трубу с неподвижной диафрагмой. Справа от диафрагмы находится газ с параметрами, отмеченными индексом 0, слева – газ 1 (см. рис. 1.15). Так как диафрагма неподвижна, то из условий “прилипания”

. (5.1.1)

В начальный момент диафрагма мгновенно убирается и образуется разрыв, параметры газов слева и справа от которого новые, – произвольный разрыв. Пусть давление слева больше давления справа

. (5.1.2)

Рис. 1.16.

В этом случае газ, находящийся слева, давит на газ справа как поршень. В свою очередь, газ, находящийся справа, тянет за собой газ слева. В результате вправо побежит ударная волна, а влево – волна разрежения. Так как эти процессы протекают очень быстро и за это время процессы диффузии не успевают произойти, то между газами образуется контактный разрыв, движущийся вправо, так как оба газа движутся вправо. Весь описанный процесс удобно изображать на диаграмме (рис. 1.16). О направлении распространения ХВР заранее ничего сказать нельзя. Он может двигаться как влево, так и вправо, потому что относительно газа ХВР движется с местной скоростью звука c, но отношение скорости газа за ударной волной к местной скорости звука c может быть как больше, так и меньше единицы (см. п. 3.3).

Найдем отношение скорости газа за ударной волной к местной скорости звука в неподвижной системе координат и покажем, что оно может быть как больше, так и меньше единицы. Используем соотношение (3.3.5)

(5.1.3)

и выражение для скорости звука

. (5.1.4)

Тогда

.

Из уравнения ударной адиабаты найдем

.

В результате получим

. (5.1.5)

Очевидно, что последнее выражение может быть как больше (при ), так и меньше (при ) единицы.

Контактный разрыв КР движется вместе с газами со скоростью , ХВР – с меньшей скоростью , поэтому он отстаёт от КР.

Найдем решение задачи о распаде произвольного разрыва. Будем обозначать параметры за ударной волной индексом “s” (shock), а за волной разрежения – индексом “r” (rarefy). Скорости за ударной волной и за волной разрежения (за ХВР) должны совпадать, так как на контактном разрыве скорость непрерывна:

. (5.1.6)

Точно такое же условие справедливо для давления

Рис. 1.17.

. (5.1.7)

На рис. 1.17 схематически нарисованы графики скорости и давления в некоторый момент времени. Волна разрежения распространяется влево, поэтому согласно (4.1.16)

. (5.1.8)

За ударной волной, распространяющейся вправо, согласно (3.3.6)

. (5.1.9)

Исключим в (5.1.9) , используя уравнение ударной адиабаты (2.2.12). Получим

. (5.1.10)

За волной разрежения давление находится по формуле, следующей из соотношений (4.1.21):

, (5.1.11)

где и начальные давление и скорость звука в газе, находящемся слева от диафрагмы. Из (5.1.6), (5.1.7), (5.1.10) и (5.1.11) можно получить нелинейное уравнение для давления

. (5.1.12)

Решая его численно, найдем , а следовательно, и . Тогда по формуле (5.1.10) легко найти .Газ за ХВР движется с такой же скоростью.

Скорость ударной волны находится из соотношений на скачке

. (5.1.13)

Из соотношений на скачке следует выражение для плотности газа за ударной волной

. (5.1.14)

А из уравнения Клапейрона-Менделеева находится температура

. (5.1.15)

Плотность газа в волне разрежения можно найти из уравнения адиабаты Пуассона

, (5.1.16)

а температуру – из уравнения Клапейрона-Менделеева

. (5.1.17)

Таким образом, все искомые параметры найдены. Следует заметить, что на контактном разрыве . Если , то .

Мы рассмотрели распад произвольного разрыва, когда слева и справа от диафрагмы был один и тот же газ. В случае двух видов газов с разными показателями адиабаты задача решается аналогично.