1.4. Волна разрежения

В этом параграфе рассмотрим волну разрежения в газе, жидкости и пузырьковой жидкости.

1.4.1. Волна разрежения в совершенном газе

Выпишем систему уравнений гидродинамики:

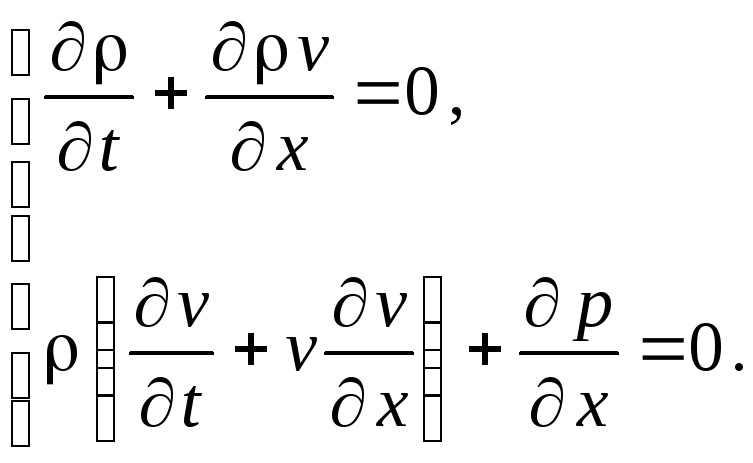(4.1.1)

Введем новую переменную

. (4.1.2)

Тогда

,

,

В результате из (4.1.1) получим

где ' – обозначает производную по .

Используя (4.1.2), найдем

(4.1.3)

Таким образом, система уравнений в частных производных (4.1.1) перешла в систему обыкновенных дифференциальных уравнений (4.1.3). В этом случае задача по решению системы (4.1.1) или (4.1.3) и ее решение называются автомодельными.

В качестве замыкающего систему (4.1.3) соотношения возьмем

или . (4.1.4)

Систему уравнений (4.1.3) и (4.1.4) преобразуем к виду

(4.1.5)

Найдем решение системы (4.1.5). Выразим из первого уравнения (4.1.5) и подставим во второе, получим

.

Следовательно,

и

. (4.1.6)

Исключая из системы уравнений (4.1.5) , получим

. (4.1.7)

Знаку “+” в (4.1.6) соответствует знак “–” в (4.1.7) и наоборот. В этом можно убедиться, подставив (4.1.7) в систему (4.1.5). Используя (4.1.4), интеграл (4.1.6) можно преобразовать к виду

. (4.1.8)

Процесс расширения газа является изоэнтропическим, и в качестве его уравнения состояния примем адиабату Пуассона

. (4.1.9)

Скорость звука

. (4.1.10)

С учетом (4.1.9) имеем

. (4.1.11)

Подставим (4.1.11) в (4.1.6). Тогда после интегрирования в пределах от до получим

. (4.1.12)

Рассмотрим волну разрежения, т. е. пусть , тогда в силу (4.1.9) и в силу (4.1.11).

Рассмотрим решение со знаком “+”:

(4.1.13)

Из (4.1.13) следует, что и

. (4.1.14)

Рассмотрим решение со знаком “–”:

(4.1.15)

В этом случае и

. (4.1.16)

Выражения (4.1.13) и (4.1.15) можно объединить:

. (4.1.17)

Поскольку , то

. (4.1.18)

Это неравенство определяет максимально достижимую скорость газа в волне разрежения.

Таким образом, существует два решения (см. рис. 1.11):

1). газ течёт влево:

Рис. 1.11.

(4.1.19)

2). газ течёт вправо:

(4.1.20)

Остальные параметры можно найти, используя уравнение адиабаты Пуассона и (4.1.11):

, , . (4.1.21)

1.4.2. Задача о выдвигающемся поршне в газе

Рис. 1.12.

Рассмотрим следующую задачу. В трубе, не ограниченной справа, находится покоящийся газ (см. рис. 1.12). Слева – поршень. В начальный момент времени поршень начинает выдвигаться из трубы с постоянной скоростью .

Требуется описать возникающее течение газа. Очевидно, что при выбранном направлении движения поршня газ потечёт влево (), а возмущение (волна разрежения) побежит по газу вправо.

Скорость газа в волне разрежения ограничена неравенством (5.1.8):

.

Рассмотрим два случая

а). Скорость поршня не превышает максимальную скорость газа в волне разрежения

. (4.2.1)

Тогда скорость газа вблизи поршня определяется условием “прилипания”:

. (4.2.2)

Поэтому соотношения (4.1.19) в этом случае примут вид:

. (4.2.3)

Рис. 1.13

При скорость газа остается постоянной и равной скорости поршня . Полученное автомодельное решение изображено на рис. 1.13.

Проанализируем полученное решение. Точка (см. рис. 1.13) носит название “головы волны разрежения” (ГВР) и движется по невозмущенному газу вправо со скоростью звука . Точка – “хвост волны разрежения” (ХВР). ХВР может двигаться как вправо, если (или ), так и влево, если .

Найдем скорость ХВР относительно газа. Скорость газа . Скорость ХВР .

Их разность как раз и будет искомой скоростью

. (4.2.4)

Последнее равенство в (4.2.4) написано на основании решения (4.1.13).

Таким образом, ХВР движется относительно газа вправо с местной скоростью звука.

б). Скорость поршня больше максимальной скорости газа в волне разрежения:

. (4.2.5)

В этом случае справедливы соотношения (4.1.19). Точка (ГВР) имеет координату (рис. 1.14), но (ХВР) имеет координату . Координата поршня . Поршень отрывается от газа, и между поршнем и ХВР газ отсутствует (вакуум). Скорость ХВР относительно газа равна нулю.

Рис. 1.14.