1.1.2. Уравнение состояния пузырьковой жидкости в термодинамически равновесном приближении с учетом сжимаемости несущей фазы

В случае очень малого содержания пузырьков или большой интенсивности волны необходимо учитывать сжимаемость жидкости. Получим уравнение состояния пузырьковой жидкости в термодинамически равновесном приближении с учетом сжимаемости несущей фазы.

Повторим выкладки предыдущего параграфа, заменив выражение (2.1.14) на акустическое уравнение состояния несущей фазы (жидкости)

. (1.2.1)

Здесь – скорость звука в жидкости. Тогда выражение (1.1.18) примет вид

. (1.2.2)

Используя , , найдем

.

Это выражение после простых алгебраических преобразований приводится к виду:

, . (1.2.3)

Это и есть уравнение состояния пузырьковой жидкости с учетом сжимаемости несущей фазы. Видно, что при (1.2.3) переходит в (1.1.20).

1.1.3. Уравнение состояния пузырьковой жидкости в термодинамически равновесном приближении с учетом поверхностного натяжения

В случае, когда пузырьки очень маленькие, когда лапласово давление сравнимо с давлением в системе , необходимо учитывать их поверхностное натяжение. Получим еще одно уравнение состояния пузырьковой жидкости с учетом поверхностного натяжения, но считая, что несущая фаза несжимаема

. (1.3.1)

Если объемная концентрация газа мала , то можно приближенно считать давление в смеси равным давлению в жидкости

. (1.3.2)

Тогда соотношение (1.1.10) примет вид

. (1.3.3)

Уравнение состояния газа (1.1.13) запишется так:

. (1.3.4)

Выражение (1.1.17) с учетом несжимаемости несущей фазы и при отсутствии фазовых переходов перепишется следующим образом:

.

Учитывая определение массовой концентрации фаз (1.1.8), получим

. (1.3.5)

Подставляя в (1.3.5) , выраженную из (1.3.4), и используя определение объемной концентрации газовой фазы (1.1.5), найдем

. (1.3.6)

В выражении (1.3.6) радиус пузырька выступает в роли параметра.

Так как масса пузырька постоянна, то изменение радиуса связано с изменением плотности формулой

. (1.3.7)

Подставляя в (1.3.5) из (1.3.7), получим

. (1.3.8)

Уравнение (1.3.4) с учетом (1.3.7) примет вид

.

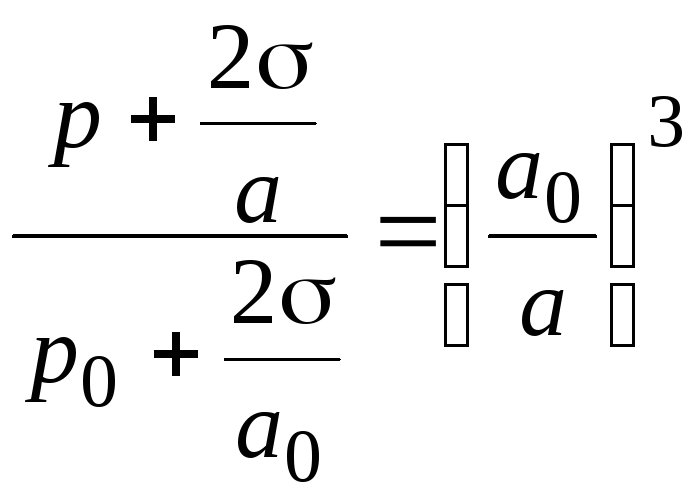Вводя обозначение

, (1.3.9)

из последнего выражения получим

. (1.3.10)

Из (1.3.8) следует выражение для плотности

. (1.3.11)

Выражения (1.3.10) и (1.3.11) вместе образуют параметрическую форму записи уравнения состояния пузырьковой жидкости без учета сжимаемости несущей фазы, но с учетом лапласова давления.

1.1.4. Скорость звука в жидкости, газе и пузырьковой жидкости

Важной характеристикой среды является скорость звука. Получим выражения для скорости звука в газе и пузырьковой жидкости.

Скорость звука в жидкости. Опыт показывает, что скорость звука в жидкости слабо зависит от изменения давления, и в широком диапазоне давлений ее можно считать постоянной.

Скорость звука в газе. Адиабатическим уравнением состояния совершенного газа (адиабата Пуассона (Poisson)) является

, (1.4.1)

Рис. 1.2.

где – показатель адиабаты газа (рис. 1.2). По определению квадрат скорости звука находится по формуле

. (1.4.2)

При начальных значениях давления и плотности получим

. (1.4.3)

Выражение (1.4.3) можно получить также другим путем. Линеаризуем (1.4.1), полагая, что , :

. (1.4.4)

Откуда для возмущений давления и плотности получим связь

. (1.4.5)

Следовательно,

.

Скорость звука в пузырьковой жидкости. Примем уравнение состояния пузырьковой жидкости в виде

, или . (1.4.6)

Скорость звука может быть выражена через удельный объем

, . (1.4.7)

Следовательно,

, . (1.4.8)

Выражение для можно получить иначе. Запишем (1.4.6) в виде

,

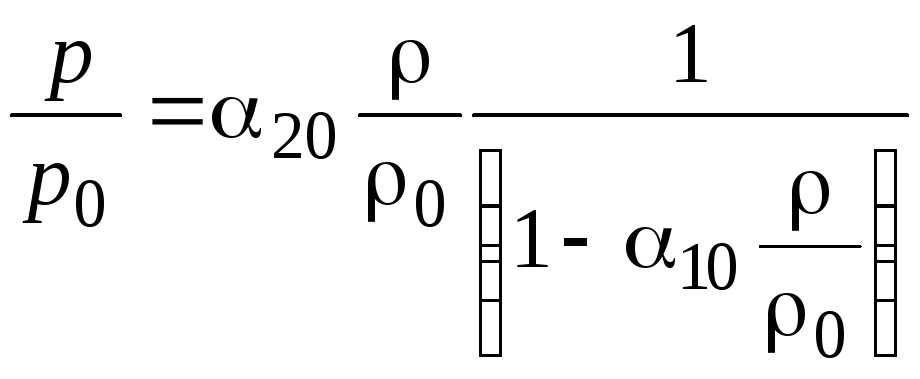После линеаризации имеем

,

или

,

таким образом

. (1.4.11)

Рис.1.3.

На рис. 1.3 показан вид зависимости давления от плотности и скорости звука от объемного содержания газа.