1. Равновесная газожидкостная система
В этой главе рассматриваются уравнение состояния газожидкостной системы в термодинамически равновесном приближении, соотношения на разрыве, задачи об ударных волнах и волнах разрежения, о волновом истечении в окружающее пространство.
1.1. Уравнение состояния и скорость звука
Получим уравнение состояния газожидкостной системы в термодинамически равновесном приближении в случаях, когда жидкость считается сжимаемой или несжимаемой, с учетом и без учета поверхностного натяжения на границе газ-жидкость.
1.1.1. Уравнение состояния пузырьковой жидкости в термодинамически равновесном приближении
Рассмотрим жидкость с пузырьками газа. Пусть пузырьки имеют одинаковый радиус и равномерно распределены по объему.
Будем
отмечать параметры, относящиеся к
жидкости и газу, индексами 1 и 2
соответственно. Здесь и далее
,
,
(
)
– скорость, давление и температура i-ой
фазы. По определению
,
(1.1.1)
–
истинные
плотности жидкости и газа (
,
– масса i-ой
фазы и объем, занимаемый ею),
,
(1.1.2)
–
приведенные
плотности фаз (
– объем смеси). Так как масса смеси
складывается из масс фаз
,
то средняя плотность смеси
,
. (1.1.3)
Введем понятие объемной концентрации фазы в смеси
,
. (1.1.4)
Тогда, учитывая (2.1.1) и (2.1.2), легко получить, что
,
. (1.1.5)
Так
как
,
то
. (1.1.6)
Для
пузырьковой жидкости характерное
объемное содержание пузырьков
.
При росте концентрации
пузырьковая жидкость превращается в
пену, а затем – в газокапельную среду
(происходит инверсия структуры потока).
Можно ввести также массовую концентрацию фазы:
,
,
. (1.1.7)
Массовые и объемные концентрации связаны соотношениями:
,
. (1.1.8)
Смесь
в целом, кроме плотности
,
характеризуется следующими параметрами:
среднемассовой скоростью
,
,
температурой
,
и средним по объему давлением
.
При уменьшении размеров пузырьков
начинают проявляться эффекты поверхностного
натяжения, что приводит к дополнительному
увеличению давления в пузырьке по
сравнению с давлением в жидкости на
величину лапласова (капиллярного)
давления
, (1.1.9)
где
– коэффициент поверхностного натяжения,
– радиус пузырька. Однако в силу малости
коэффициента поверхностного натяжения
лапласово давление можно не учитывать,
пока
или
.
Так, например, для воды
и при
критический радиус
.
В общем случае среднее давление в смеси находится по формуле
. (1.1.10)
Пузырьковая жидкость обладает следующими особенностями:
а)
высокая плотность, приближающаяся к
плотности жидкости
;
б)
высокая сжимаемость:
или
,
где
– коэффициент сжимаемости, величина,
обратная модулю объемной упругости
.
Так,
например, в водовоздушной смеси при
,
,
скорость звука
.
в)
малый акустический импеданс (волновое
сопротивление), характеризующий
“жесткость” среды,
,
;
г)
сильная нелинейность диаграммы сжатия
.
Получим
баротропное уравнение состояния
пузырьковой смеси
,
находящейся в термодинамическом
равновесии. Последнее означает, что
,
,
. (1.1.11)
При рассмотрении волновых процессов жидкость, в силу большой теплоемкости, можно считать термостатом, т.е.
. (1.1.12)
Тогда из уравнения Клапейрона (Clapeyron) - Менделеева для газа в пузырьке
следует
. (1.1.13)
Здесь
и
– давление и плотность газа в начальном
состоянии.
Сжимаемость газа значительно выше сжимаемости жидкости. Поэтому сжимаемость смеси определяется сжимаемостью газа в пузырьках, а сжимаемостью жидкости можно пренебречь, т.е. считать жидкость несжимаемой
. (1.1.14)
Будем считать, что фазовые переходы отсутствуют. Следовательно, как масса отдельного пузырька, так и массовые концентрации фаз постоянны:
,
. (1.1.15)
Из (2.1.8) выразим объемные концентрации:
,
. (1.1.16)
Учитывая (2.1.6), получим
. (1.1.17)
Подставим
из (2.1.13) в (2.1.17) и учтем (2.1.15):
. (1.1.18)
Так
как
,
,
то
.
Отсюда находим уравнение состояния
. (1.1.19)
Рис.
1.1.
:
,
,
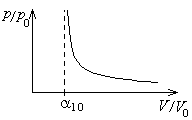
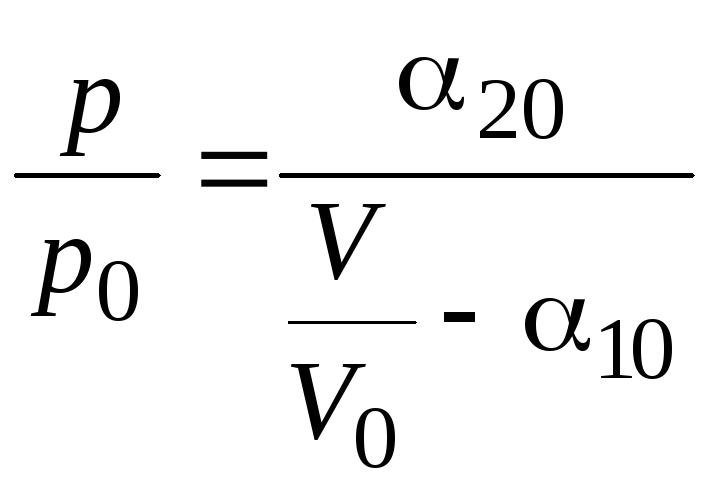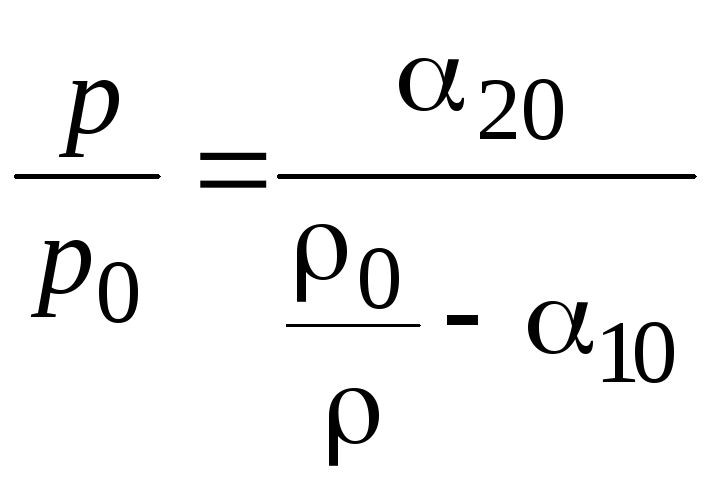. (1.1.20)
Зависимость
при
имеет асимптотику
(см. рис. 1.1).