
- •Глава 5 Линейные и квадратичные формы
- •§ 5.1 Линейная форма
- •§ 5.2 Уравнение гиперплоскости в Rn
- •§ 5.3 Уравнение прямой в r3
- •§ 5.4 Примеры задач на прямую и плоскость в r3
- •§ 5.5 Квадратичные формы Определение 1. Квадратичной формой от n переменных называется однородная функция второго порядка вида
- •§ 5.6 Диагональная квадратичная форма Определение 1. Квадратичная форма вида
- •С диагональной матрицей коэффициентов называется диагональной. При этом вид (1) называется каноническим видом квадратичной формы.
- •§ 5.7 Критерий Сильвестра
- •§ 5.8 Уравнение линий второго порядка
- •§ 5.9 Уравнение поверхностей второго порядка
§ 5.7 Критерий Сильвестра
Определение
1.
Будем
говорить, что квадратичная форма
![]() положительна
(отрицательна),
если положительны (отрицательны) все
ее значения при вещественных значениях
переменных, не равных нулю одновременно
(нулевые
значения отсутствуют).
положительна
(отрицательна),
если положительны (отрицательны) все
ее значения при вещественных значениях
переменных, не равных нулю одновременно
(нулевые
значения отсутствуют).
Например, форма f(х1,x2) = х12 + x22 положительна, а форма f(х1,x2)=-3х12 – 4x22 отрицательна.
Из примеров видно, что положительность или отрицательность формы легко определима при ее каноническом представлении.
Определение
2.
Будем
говорить, что квадратичная форма
![]() неотрицательна
(неположительная),
если
неотрицательна
(неположительная),
если
![]()
Определение
3.
Будем говорить, что квадратичная форма
![]() знакопеременна,
если она принимает на
знакопеременна,
если она принимает на
![]() как положительные, так и отрицательные
значения.
как положительные, так и отрицательные
значения.
Определение
4.
Будем
обозначать через
![]() угловой
минор
порядка k
матрицы А,
т.е. минор расположенный на пересечении
k
первых строк и k
первых столбцов матрицы А.
угловой
минор
порядка k
матрицы А,
т.е. минор расположенный на пересечении
k
первых строк и k
первых столбцов матрицы А.
Теорема 1 ( критерий Сильвестра)
Пусть
дана квадратичная форма
![]() .
Данная
форма:
.
Данная
форма:
-
положительна тогда и только тогда, когда
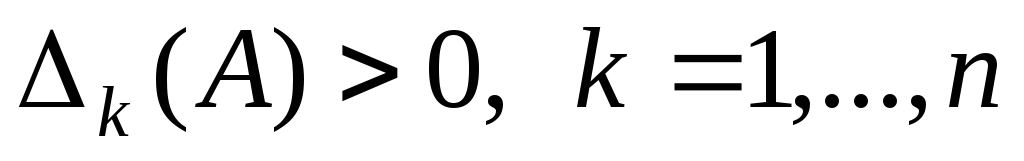 ;
;
-
отрицательна тогда и только тогда, когда
 ;
; -
неотрицательна тогда и только тогда, когда
 ;
; -
неположительная тогда и только тогда, когда
 ;
;
-
знакопеременна – в остальных случаях.
Неотрицательные и неположительные форма иногда называют полуопреленными.
Если в результате ортогональных преобразований квадратичная форма приведена к диагональному виду, то для определения ее знакоопределенности можно использовать следующую теорему.
Теорема
2.
Вещественная квадратичная форма
![]() является
положительной (отрицательной) тогда и
только тогда, когда она ортогональным
преобразованием переменных может быть
приведена к чистой сумме (разности)
квадратов, т.е к виду
является
положительной (отрицательной) тогда и
только тогда, когда она ортогональным
преобразованием переменных может быть
приведена к чистой сумме (разности)
квадратов, т.е к виду
![]() (
(![]() )
)
§ 5.8 Уравнение линий второго порядка
Определение 1. Многочлен вида
![]() (1)
(1)
представимый в виде суммы квадратичной формы, линейной формы и свободного члена называют многочленом второй степени от n переменных.
В матричной форме многочлен (1) можно записать в виде
Ф(Х) = ХТАХ + 2ХТВ + С
Записи
![]() и ХТАХ
+ 2ХТВ
+ С = 0 (2)
и ХТАХ
+ 2ХТВ
+ С = 0 (2)
называют общим уравнением второй степени.
Определение 2. При n = 2 уравнение (2)называют уравнением линии второго порядка на плоскости в декартовой системе координат.
Многочлен Ф(Х) при этом примет вид:
Ф(x1x2) = Ax12 + Bx22 + 2Cx1x2 + 2Dx1 + 2Ex2 + 2F (3)
Каждой линии 2-го порядка отвечает симметричная матрица вида
![]() .
.
Верно и обратное – каждой симметричной матрице 3-го порядка отвечает единственная линия 2-го порядка. Определитель такой матрицы называют главным дискриминантом линии 2-го порядка.
Так как выражение (1) представляет собой сумму комбинацию квадратичной и линейной формы, то используя теорему Лагранжа получаем результат
Теорема 1 С помощью невырожденных преобразований (в тои числе и ортогональных) любое уравнение Ф(x1x2)=0 линии 2-го порядка в надлежащей системе координат приводится к одному из двух видов
Ф(у1у2) = у12 + y22 + или Ф(у1у2) = у12 + 2y2
При этом, в зависимости от значений полученных коэффициентов различают:
-
у12 - y22 = 0 две пересекающихся прямых
-
у12 = 1 две параллельные прямых
-
у12 + y22 = 1 эллипс
-
у12 - y22 = 1 гипербола
-
у12 = 2y2 парабола.
Для того, чтобы линия второго порядка сводилась к 2-м прямым необходимо и достаточно, чтобы главный дискриминант кривой второго порядка был равен нулю.
Пример. Пусть задана линия
Ф(x1x2) = -2x12 + х22 + 2x1x2 - 4x1 + 2x2 – 2
Записав ее матрицу получим, что главный дискриминант равен нулю. Запишем выражение от переменной х2:
х22 + x2(2х1 + 2)- 2(x1 + 1)2 = 0
Решая
уравнение относительно х2,
получаем выражение для двух прямых:
х2
=(х1+1)±
![]() (х1+1)
(х1+1)
Рассмотрим геометрические образы трех фигур – эллипса, гиперболы и параболы.
-
Эллипсом называется линия, имеющая в заданной системе
координат уравнение
![]() ,
где х,y
– переменные; a,b
положительные числа.
,
где х,y
– переменные; a,b
положительные числа.
Ее геометрический образ имеет вид

b



 -a
F1
F2
a
-a
F1
F2
a

 -c
c
-c
c
-b
Отрезок [-a,a] называют большой осью, отрезок [-b,b] малой осью.
Точки F1 и F2 называют фокусами, их координата определяется:
с
=
![]() .
.
Сумма расстояний от фокусов до любой точки эллипса постоянная величина, равная 2а.
Отношение координаты фокуса к большой оси эллипса называется его эксцентриситетом е и определяется по формуле е = с/a.
Ясно, что 0 < е < 1. Если a = b, то эллипс является окружностью.
Пример. Рассмотрим производственную функцию зависимости объема производства от ресурсов 2-х видов: f(x,y)=40x + 72y –4x2 –9y2.
Необходимо выяснить, при каких ресурсах x,y объем производства равен 208 единиц.
Решение. Искомая функция 40x + 72y – 4x2 – 9y2 = 208. Произведем преобразование:
-4(x2 – 10х + 25) – 9(у2 – 8у + 16)+244 = 208
или -4(x – 5х)2 – 9(у – 4)2 = -36
или
![]()
Например, объем производства в 208 единиц достигается при значениях ресурсов х = 2, у = 4.
2. Гиперболой называется линия, имеющая в некоторой системе координат уравнение
![]() , где
х, y
– переменные, a,
b
положительные числа.
, где
х, y
– переменные, a,
b
положительные числа.
Ее геометрический образ имеет вид
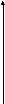

 Y
=-
Y
=-![]() х
Y
=
х
Y
=![]() х
х


b





 -c
-a
a
c
-c
-a
a
c


F1 F2
 -b
-b
Отрезок
[-a,a]
называют действительной
осью, отрезок [-b,b]
мнимой
осью. Линии Y
=-![]() х
и Y
=
х
и Y
=![]() х
называются асимптотами
гиперболы.
Точки F1
и F2
называют фокусами,
их координата определяется: с =
х
называются асимптотами
гиперболы.
Точки F1
и F2
называют фокусами,
их координата определяется: с =
![]() .
.
Модуль разности расстояний от фокусов до любой точки гиперболы постоянная величина, равная 2а.
Отношение координаты фокуса к действительной оси гиперболы называется его эксцентриситетом е и определяется по формуле
е = с/a, е > 1.
Равносторонней называется гипербола, у которой a = b.
3. Параболой называется линия, имеющая в системе координат уравнение у =ах2, р>0.



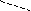
 M(x,
ax2)
M(x,
ax2)
F

 N(x,-1/4a)
Y
= -
N(x,-1/4a)
Y
= -![]()
Точка
F(0,
![]() )
называется фокусом
параболы, а прямая
)
называется фокусом
параболы, а прямая
Y
= -![]() ее директрисой.
Все
точки параболы одинаково удалены от
фокуса и от директрисы.
ее директрисой.
Все
точки параболы одинаково удалены от
фокуса и от директрисы.
