
Глава 6 Теория линейных операторов
§ 6.1 Линейные операторы в конечномерных пространствах
Определение 1. Линейным
оператором
![]() ,
действующим в векторном
пространстве
,
действующим в векторном
пространстве
![]() над числовым полем К (или линейным
преобразованием векторного
пространства
над числовым полем К), называется
правило, по которому
каждому вектору
над числовым полем К (или линейным
преобразованием векторного
пространства
над числовым полем К), называется
правило, по которому
каждому вектору
![]() ставится в соответствие определенный
вектор
ставится в соответствие определенный
вектор
![]() :
:
![]() ,
причем для любых векторов
,
причем для любых векторов
![]() и любого числа
и любого числа
![]() из поля К выполняются
равенства:
из поля К выполняются
равенства:
![]() (аддитивное свойство);
(аддитивное свойство);
![]() (свойство однородности).
(свойство однородности).
При этом используют следующую
терминологию: вектор
![]() называют образом вектора
называют образом вектора
![]() при данном линейном преобразовании
(или результатом действия оператора
на вектор
),
вектор
называют прообразом
вектора
.
при данном линейном преобразовании
(или результатом действия оператора
на вектор
),
вектор
называют прообразом
вектора
.
Фактически линейный оператор можно рассматривать, как векторную функцию, т.е. функцию, заданную на векторном пространстве . Механизмом, реализующим действие линейного оператора , является его матричное представление.
Пусть в векторном
пространстве
![]() фиксирован некоторый базис
фиксирован некоторый базис
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
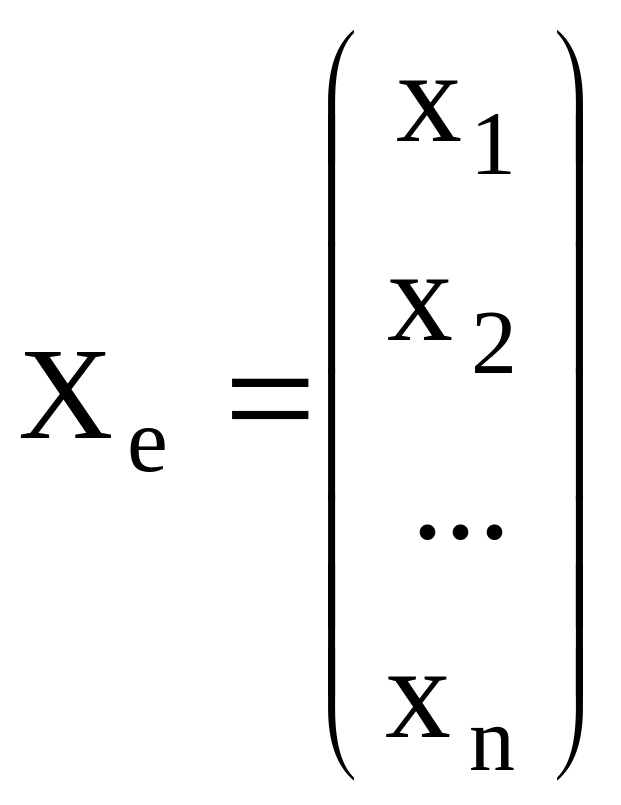 ,
- разложение произвольного вектора
,
- разложение произвольного вектора
![]() по базису Е. Рассмотрим
действие оператора
к векторам
по базису Е. Рассмотрим
действие оператора
к векторам
![]() .
.
Разложение вектора
![]() по базису
имеет вид:
по базису
имеет вид:
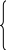 f1=
f1=![]() ,
,
f2=![]() ,
(1)
,
(1)
. . . . . . . . . . . .
fn=![]() .
.
Матрицу
 называют матрицей
оператора
называют матрицей
оператора
![]() в базисе Е
или матрица
линейного преобразования
в базисе Е
и обозначают Ае.
в базисе Е
или матрица
линейного преобразования
в базисе Е
и обозначают Ае.
Равенство (1) переводит векторы Е, составляющие базис пространства, в систему векторов F, причем полученные вектора остаются в исходном базисе Е. Эту операцию можно записать в матричном виде
![]() или
или
![]() ,
,
где
![]()
![]() =
F
- матрица-строка, состоящая из образов
базисных векторов E.
=
F
- матрица-строка, состоящая из образов
базисных векторов E.
Рассмотрим основные операторы и их матричные аналоги:
Оператор
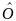 ,
действующий по правилу
,
действующий по правилу
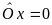 для любого элемента
,
для любого элемента
,
называется нулевым оператором и ему соответствует нулевая матрица.
Оператор
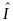 ,
действующий по правилу
,
действующий по правилу

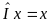
,
называется тождественным
(единичным)
оператором и ему
соответствует единичная матрица.
,
называется тождественным
(единичным)
оператором и ему
соответствует единичная матрица.Оператор
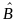 называется обратным к
оператору
,
если
называется обратным к
оператору
,
если
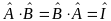 и ему соответствует обратная к А
матрица, обозначаемая А-1.
и ему соответствует обратная к А
матрица, обозначаемая А-1.Суммой
 =
=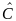 линейных операторов
и
называют оператор
такой, что
линейных операторов
и
называют оператор
такой, что
![]() и оператору С
соответствует сумма матриц А
+ В.
и оператору С
соответствует сумма матриц А
+ В.
Произведением
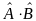 =
линейных операторов
и
называется оператор
,
=
линейных операторов
и
называется оператор
,
которому соответствует
произведение матриц А,В:
![]() .
.
6. Операторы и называются равными, если равны их матрицы А и В.
Для линейных операторов выполняются все свойства, свойственные матрицам, т.е. линейные операторы образуют линейное пространство.
Теорема. Если переход
от базиса
![]() к базису
к базису
![]() ,
осуществляется по формуле
,
осуществляется по формуле
![]() ,
где
,
где
![]() - матрица перехода между
базисами (или матрица
пересечения базисов),
то матрица оператора
преобразуется по формуле:
- матрица перехода между
базисами (или матрица
пересечения базисов),
то матрица оператора
преобразуется по формуле:
![]() или
или
![]() (2).
(2).
Замечание. Теорема имеет наглядный геометрический смысл: рассмотрим двумерную
декартовскую систему с двумя базисами

 Yf
Yf

 Xe
Ae
Xe
Ae
Pef
 Ye
Ye

Система с базисом е Система с базисом f
последовательность действий: АeXe = Ye,Pef(Ye)= Yf или Pef(Ae)=Yf
Xf

Xe Af
Pef Yf
Система с базисом е Система с базисом f
или PefXe = Xf, АfXf = Yf или Аf(Pef) = Yf и приравнивая левые части получим: PefAe = АfPef или и .
Найти матрицу преобразования в базисах E, F при обратном переходе от базису к базису .
Пример.
Задан оператор
 е
с матрицей
е
с матрицей
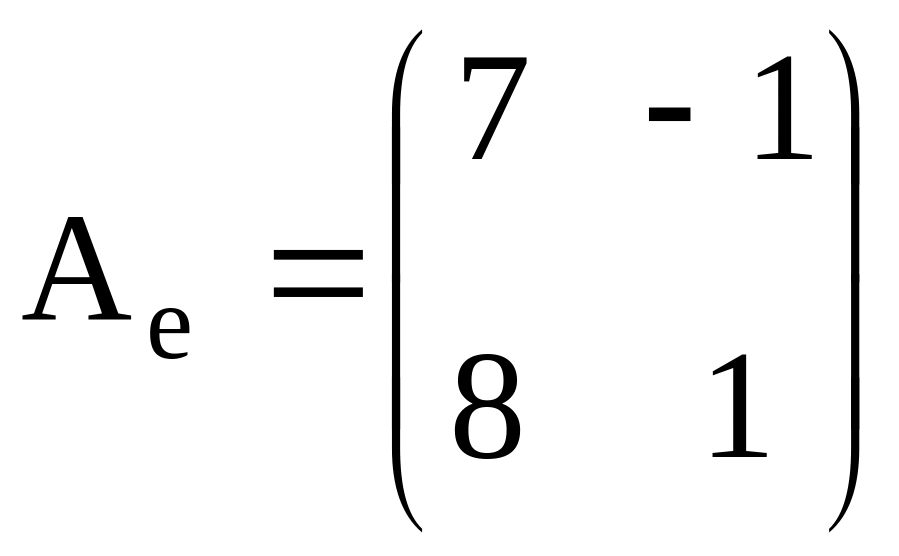 и матрица перехода
и матрица перехода
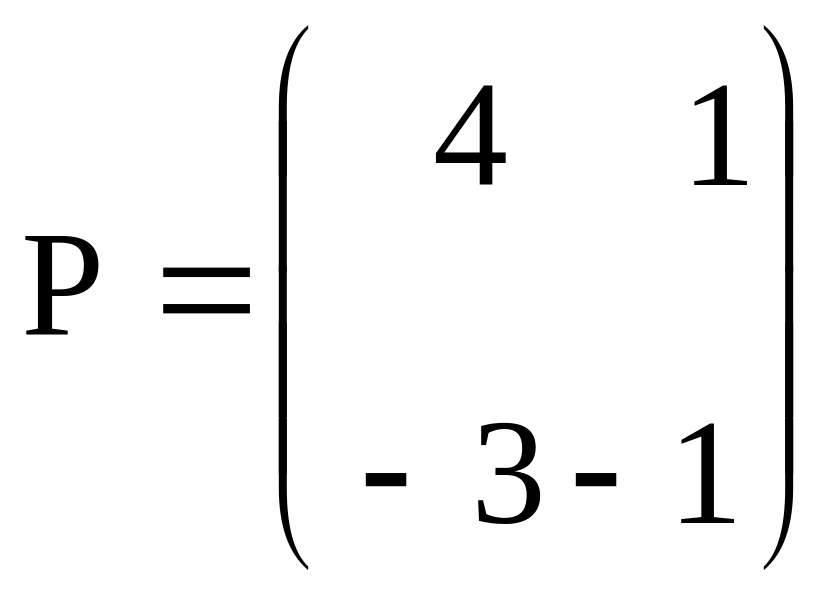 от
от
базиса
![]() к базису
к базису
![]() .
Вычислить матрицу оператора
.
Вычислить матрицу оператора
![]() и найти
и найти
образ
![]() вектора
вектора
![]() в базисе
двумя способами.
в базисе
двумя способами.
Решение. Находим
матрицу, обратную к Р:
![]() .
Находим матрицу оператора
:
=
.
Находим матрицу оператора
:
=
![]() .
Тогда
.
Тогда
![]() =
=![]() =
=![]() и Рef(
)=
=
и Рef(
)=
=![]() .
.
С другой стороны, Рef(![]() =
=![]() =
=![]() и
и
![]() =
.
=
.
