§ 2.3 Ранг матрицы

Пусть в матрице размера m x n выбраны произвольно k строк и k столбцов, причем k  min(m, n). Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором k-ого порядка матрицы .

Количество миноров k-го порядка в матрице (m,n) определяется по формуле , где Сⁱ_j – называют сочетаниями из j элементов по i элементам (число различных поднаборов из k элементов, выбранные из исходных n элементов),

Пример. В матрице 4х5 число миноров 3-го порядка будет равно

Теорема 1. Если в матрице все миноры k-го порядка равны нулю, то равны нулю и все миноры более высоких порядков.

Доказательство теоремы следует из разложения любого минора (k+1) порядка по любой строке или столбцу: так как все миноры порядка k равны нулю, то и сумма произведений элементов строки на миноры порядка k равны нулю.

Определение 1. Максимальный порядок r отличных от нуля миноров матрицы называется ее рангом и обозначается .

Пример. Ранг матрицы А= равен 2, а ранг матрицы В=

равен 1, так как все миноры 2-го порядка равны нулю.

Определение 2. Если ранг матрицы равен r, то отличные от нуля миноры порядка r называют базисными (их может быть несколько). Строки и столбцы, на пересечении которых расположен базисный минор, называют базисными строками и столбцами.

Пример. В матрице А = с рангом 2 присутствуют 3 минора

порядка 2, из них 2 базисных минора. Базисными строками будет 1 и 3, 3 и 4, но не будет 1 и 4, т.к. этот минор 2-го порядка равен нулю. Базисными столбцами будут 1-ый и 3-ий.

Замечание. Если все элементы матрицы равны нулю, то .

Основными методами вычисления ранга матрицы являются метод элементарных преобразований и метод окаймляющих миноров.

Определение 3. Элементарным преобразованиями над строками (столбцами) матрицы называют следующие операции:

1. Умножение элементов строки на любое число отличное от нуля

2. Прибавление к строке любой другой строки

3. Перемена двух строк местами

Элементарные операции обладают следующими свойствами:

• одна операция п.3 равносильна последовательному выполнению операций п.1 и п.2 ( доказать!),

• операции обратимы, т.е. применяя операции п.1-3 переходят от матрицы А к матрицы В, обратными операциями (умножению - деление, сложению – вычитание) переходят от матрицы В к А,

• при элементарных операциях ранг матрицы не меняется.

Приведенные свойства позволяют вычислять ранги любых матриц.

Примеры. 1.Вычислим ранг матрицы методом элементарных преобразований. Помножим 1-ю и 4-ю строки на , 3-ю строку - на и переставим первую и третью строки:

.

Если из 2-ой строки вычесть 1-ю, а из 4-ой - удвоенную 1-ю строку, то получим:, .

2. Метод окаймляющих миноров строится на следующем принципе:

Если в матрице найдется минор порядка k отличный от нуля, а все содержащие его внутри себя миноры порядка (k+1) равны нулю, то ранг матрицы равен k.

Вычислим ранг матрицы . Минор второго порядка отличен от нуля. Его окаймляют (содержат внутри себя) три минора третьего порядка: , ,

и минор 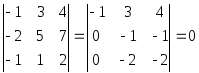, то .