Глава 2. Системы алгебраических уравнений

§ 2.1 Основные определения

Определение 1. Запись вида

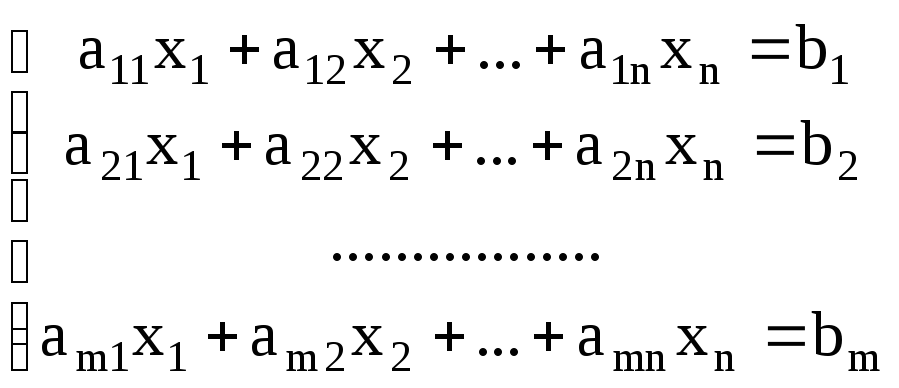(1)

системой m линейных алгебраических уравнений с n неизвестными

, где матрица называется основной

матрицей системы или матрицей из коэффициентов при неизвестных, столбцы 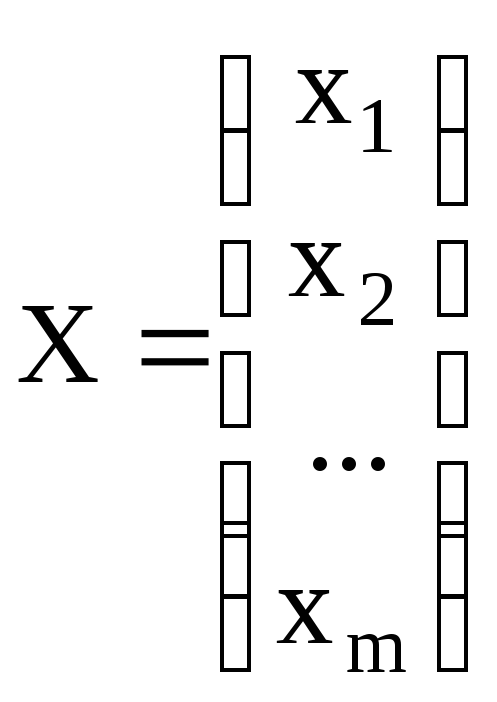и называют столбцами неизвестных и свободных (заданных) правых частей уравнений.

Определение 2. Набор чисел ₁, ₂, …,_n называется решением системы (1), если после замены неизвестных числами ₁, ₂, …,_n каждое уравнение системы обращается в равенство.

Заметим, что система уравнений (1) может быть записана в виде эквивалентного матричного уравнения (следует из определения операции умножения матриц и принципа равенства двух матриц)

(2).

В зависимости от соотношений между m и n различают:

квадратную (m =n) и прямоугольную (n  m) систему уравнений (1).

В обоих случаях для решения (1) надо ответить на два вопроса:

имеет ли система решение и если имеет, то сколько таких решений – одно или бесконечное число.

Если система не имеет решений, то ее называют несовместной, а если система имеет решение, то ее называют совместной. Если решение единственное, то система называется определенной, а если число решений более одного, то неопределенной.

В последнем случае (решений более одного) каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением (если решение единственное, то его также называют общим).

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, необходимо найти ее общее решение (единственное или бесконечное).

Две системы называются эквивалентными (или равносильными), если они имеют одно и то же общее решение (или оба не имеют решений).

§ 2.2 Методы решения квадратных систем уравнений

Пусть задана система уравнений АХ = В с квадратной матрицей из коэффициентов А.

Обозначим через символ _K определитель матрицы D_k, отличающейся от матрицы из коэффициентов А тем, что вместо элементов k-го столбца в матрице D_k стоят элементы свободных членов – столбца В:

Теорема.( Крамера ).

Пусть дана система n линейных уравнений с n неизвестными. Если определитель матрицы коэффициентов системы отличен от нуля, то система имеет единственное решение, определяемое по следующим формулам:

(1) формулы Крамера.

Доказательство. Докажем единственность решения по формулам (1)

Пусть набор чисел ₁, ₂,…, _n является решением системы АХ=В, определяемый по формулам (1). Помножим каждое i –ое уравнение системы последовательно на элементы А_i1 и сложим полученный результат. Получим следующее выражение

или  ₁ = ₁ или

Проводя такие же выкладки для каждого _i получим, что решения определяются по формулам (1). Если вместо набора ₁, ₂,…, _n выбрать числа ₁, ₂,…, _n, то получим те же формулы. Единственность доказана.

Докажем существование решения.

Выберем любое из уравнений системы и подставим вместо неизвестных их значения из формулы (1). Получим

Теорема доказана.

Пусть матрица является невырожденной и существует решение данной системы - столбец , который при подстановке в уравнение АХ = В обращает его в тождество. Умножая обе части этого тождества слева на матрицу , получим

(2)

Раскроем последнее равенство, пользуясь правилом умножения матриц и явным выражением для обратной матрицы:

.

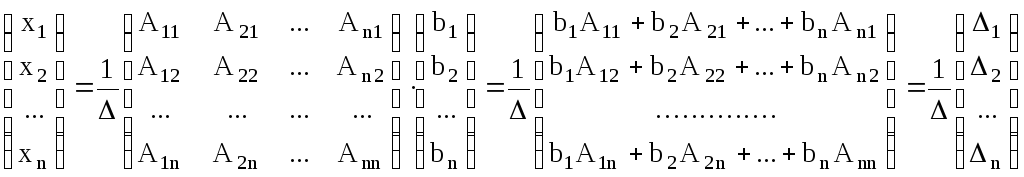Покомпонентное сравнение левого и правого столбцов равенства дает формулы Крамера .

Итак, при detA  0, решение системы АХ = В с помощью обратной матрицы неявно использует формулы Крамера. При этом надо понимать, что вычислительные аспекты каждого из двух методов различны. Выбор предпочтительного для вычислений метода не относится к нашему курсу. Интересующихся данным вопросов отправляем к работе [ ].

Пример.

Решим систему линейных уравнений двумя способами:

а) Применим для нахождения решения формулы Крамера:

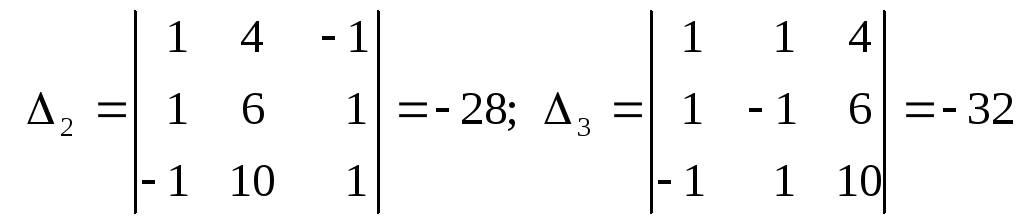
b) Применим для нахождения решения метод обратной матрицы:

Из AX = B и А^-1AX = А^-1B следует X = А^-1B

Находим взаимную матрицу: .

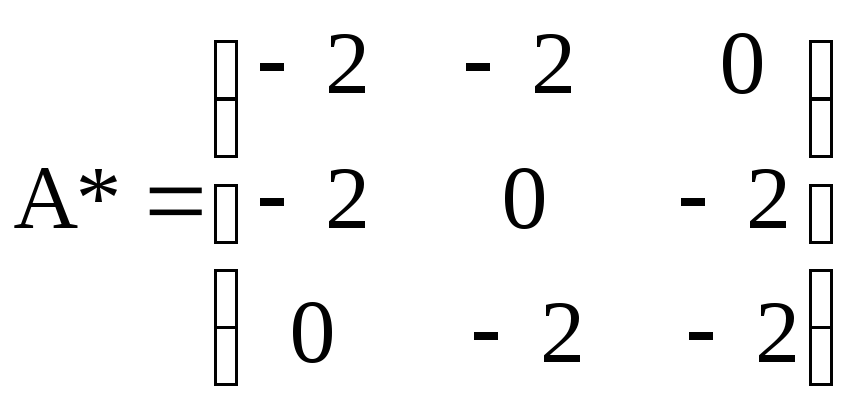Тогда X = А^-1B = =