Описание поверхностей неявными функциями

Поверхности описываются функцией вида f(X,Y,Z)=0, где X,Y,Z - координаты из пространства объекта.

Наиболее распространены функции первой и второй степени, существуют аналитические методы для решения уравнений третей и четвертой степени, однако они применяются редко.

AX+BY+CZ+D=0 описывает плоскость

7. Поточечное описание поверхностей.

Метод заключается в задании поверхности множеством принадлежащих ей точек. Следовательно, качество изображения при этом методе зависит от количества точек и их расположения.

Поточечное описание применяется в тех случаях, когда поверхность очень сложна и не обладает гладкостью, а детальное представление геометрических особенностей важно для практики.

Пример: Участки грунта на других планетах, формы небесных тел, информация о которых получена в результате спутниковых съемок. Микрообъекты, снятые с помощью электронных микроскопов.

Исходная информация о поточечно описанных объектах представляется в виде матрицы трехмерных координат точек.

8. Способы представления моделей геометрических объектов

В общем случае в любой геометрической модели можно выделить две составляющие ее части (уровни):

• набор структурных элементов. Например, в полигональной модели это вершины, ребра и грани;

• топология, т.е. собственно структура, определяющая способ взаимосвязи элементов.

Структурный элемент как геометрический объект, вообще говоря, можно представить одним из способов: 1) параметрически (функциональная зависимость координат от переменных параметров):

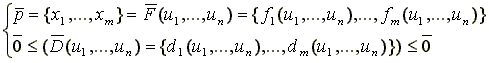
2) неявно:

где m – размерность пространства (1 – одномерное, 2 – двумерное, 3 – трехмерное);

n – размерность элемента (0 – нульмерный, определяет точку; 1 – одномерный, определяет линию; 2 – определяет поверхность);

- m-мерная вектор-функция, определяющая форму параметрического элемента;

- m-мерная вектор-функция, задающая пределы изменения параметров;

- m-мерная вектор-функция, определяющая неявное уравнение геометрического элемента;

- m-мерный нулевой вектор.

Как видно, неявное задание геометрического объекта более компактное. Тем не менее параметрическому заданию отдается предпочтение в силу его удобства для решения задач нахождения:

- точки, принадлежащей объекту;

- нормали к кривой или поверхности;

- осуществлять функции тонирования.

Классификация существующих способов представления трехмерных геометрических объектов (моделей):

- простейшие способы;

- граничное задание;

- объемное задание.

К простейшим способам задания трехмерных объектов относятся точечное и проволочное (каркасное) представления.

В точечном представлении объект задан совокупностью вершин, принадлежащих поверхности объекта V = {V1,…,Vn}.

Проволочная модель является расширением предыдущего способа. Объекты задаются совокупностью вершин и соединяющих их ребер (отрезков прямой или кривой):

V = {v₁,…,v_n}, Е = {v_i, v_j [f_k(u)]},

где f_k(u) – это элемент, используемый, если ребро не является отрезком прямой, соединяющей вершины v_i, v_j. Как правило, для одной модели f_k является вектор-функцией одного и того же типа.

Основное преимущество этих способов - простота представления. Потому они применяются на промежуточных стадиях работы с геометрическим объектом: предварительная визуализация и как исходные модели для синтеза более сложных моделей.

Поверхностное (граничное) задание моделей. Поверхностное представление объекта подразумевает точное математическое описание. Существует два основных способа описания поверхности: явное параметрическое и в виде неявных функций. Общий вид параметрической поверхности следующий:

,

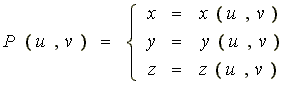где для параметров u и v, как правило, определяют область определения либо прямоугольного (u_a < u < u_b, v_a < v < v_b), либо треугольного (u_a < u < u_b, v_a < u + v < v_b) вида.

Можно выделить два основных типа поверхностных параметрических моделей:

- полигональная модель, которая представлена набором плоских граней;

- патч-модель, или лоскутная модель. В данном случае гранями служат части поверхностей одного типа (билинейные, поверхности Кунса, бикубические поверхности, поверхности Безье, поверхности на основе B-сплайнов).

Поверхностное задание трехмерных объектов является наиболее распространенным, и для него сформировались следующие разновидности топологий:

1. Список вершин. В этой топологии грань выражается через вершины:

V = {v_i } – вершины |V| = n;

F = {(v_j1, v_j2,…, v_jk [, f_j(u,v)]) } – грань (или патч f_j), состоящая из k вершин (k >= 3).

2. Список ребер. Здесь грань выражена через ребра:

V = {v_i } – вершины |V| = n;

Е = {e_k = (v_i, v_j [f_k(u)])} – ребро. f_k – уравнение линии;

F = {(e_j1, e_j2,…,e_jk [f_j(u,v)])} – грань (или патч f_j), состоящая из k ребер

(k >= 3).

3. «Крылатое» представление. Эта модель является развитием модели, основанной на информации о ребрах. Отличие состоит в том, что в структуру, описывающую ребра, добавляется информация о взаимном расположении граней. Она включает:

V = {v_i } – вершины |V| = n;

E = { e_k = (v_start, v_end, n_cw, n_ccw, [f_k(u)])} – ребро, где v_start – начало ребра, v_end – конец ребра, n_cw – следующее (предыдущее) ребро в той грани, где e_k встречается в положительном направлении обхода вершин, n_ccw – следующее (предыдущее) ребро в другой грани (где e_k встречается в отрицательном направлении);

F = { (first_edge, sign [f_j(u,v)]) } – грань (или патч f_j), где first_edge – первое ребро в цепочке представления грани, sign – знак (+/-), определяющий, в каком направлении встречается ребро first_edge в данной грани.

«Крылатое» представление является наиболее удобным для реализации важнейших алгоритмов над геометрическими объектами:

- проверка правильности задания;

- алгоритмы для полигональных моделей, связанные с обходом ребер (выделение плоских контуров, упрощение модели путем удаления граней и другие).

Кроме того, не более чем за линейное время можно восстановить любую другую топологию, следуя по цепочкам связей между элементами.

В объемном представлении базовыми являются неявно представленные примитивы. Наиболее известны:

- воксели;

- метаболы;

- сплошные конструктивы.

Основой воксельного представления служит так называемый воксель (или ячейка), представляющий собой кубическую область пространства. Трехмерный объект определяется как массив вокселей. Можно выделить следующие топологии воксельного объекта:

1. простейшая – набор одинаковых вокселей, аппроксимирующий область пространства, занимаемую объектом;

2. V = { ({L} x {M} x {N}, {1,0}) } – элементу трехмерного массива вокселей размером L x M x N ставится в соответствие его заполненность (принадлежность объекту);

3. октальное дерево – рекурсивное разбиение пространства на 8 частей. При этом устанавливается некоторый минимальный размер вокселя. Лист дерева помечается заполненным, если он полностью принадлежит объекту. Таким образом, топология представлена в виде дерева;

4. PM-октальные деревья – это гибрид октального дерева и полигональной модели для уменьшения погрешности аппроксимации при достижении минимального размера вокселя в рекурсивном разбиении пространства.

Воксельное представление является очень удобным для реализации пространственных алгоритмов и теоретико-множественных операций над объектами (объединение, вычитание, пересечение), но обладает рядом недостатков, которые ограничивают область его применения:

- низкая точность для представления для большинства

объектов;

- большой объем занимаемой памяти.

Метаболы – это шары различного радиуса (r), которые могут взаимодействовать в зависимости от близости и радиуса взаимодействия (R): Сфера = (координаты, радиус, вещество). Взаимодействие выражается через появление дополнительной «материи» между ними. Топология, как таковая, здесь отсутствует.

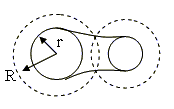
Взаимодействие двух метаболов

При представлении объекта в виде сплошных конструктивов используют два набора:

- базовый набор примитивов (параллелепипед, сфера, конус, цилиндр, тор, призма, пирамида и т.п.), являющихся структурными элементами объекта;

- базовый набор теоретико-множественных операций: унарного аффинного преобразования (T) и бинарных операций вычитания (-), пересечения (*), объединения (+). Данный набор определяет топологию модели, которая реализуется в виде формулы теории множеств.

Например, если мы имеем три примитива A, B, C и формулу (A + T(B)) * C, то это означает, что мы объединяем объект А с трансформацией объекта В и пересекаем его с объектом С. Преимущество данного способа представления заключается в том, что таким образом можно относительно легко моделировать достаточно сложные объекты.

Параметрическое задание геометрических объектов

Как упоминалось ранее, параметрическое задание подразумевает функциональную зависимость координат точек объекта от некоторых параметров. Для линий используется функция одной переменной:

p = F(u) = (F_x(u), F_y(u), F_z(u)),

а для поверхности – функция двух переменных:

p = F(u, v) = (F_x(u, v), F_y(u, v), F_z(u, v)).

Вообще говоря, вид функции F может быть произвольной. Но на практике ограничивают набор функций, которые представляют наиболее часто встречающиеся геометрические объекты, из которых затем составляют более сложные. К ним относятся:

1) плоские линии: прямые, окружности, эллипсы и их отрезки, спирали Архимеда, эквидистанты;

2) пространственные линии: спирали;

3)поверхности: плоские, сферические, цилиндрические, конические, торические, пружинные.

Как видно, их перечень невелик. А потому для моделирования кривых и поверхностей, которые не вписываются в этот набор, используются сплайны и патчи. Наиболее употребляемые виды сплайнов: сплайны Безье, B-сплайны (NURBS). Среди патчей можно выделить: патчи NURBS, Безье-патчи, N-патчи, билинейные патчи, патчи Кунса. Тем не менее большинство пакетов использует эти инструменты для аппроксимации вышеперечисленных кривых и поверхностей и не имеют автоматических средств для аппроксимации пользовательский кривых (параболы, гиперболы, синусоиды) и поверхностей (параболоиды, конусы с образующей заданного вида и др.) с помощью перечисленных сплайнов и патчей.

Основные задачи, которые должны быть при этом решены:

1) гибкость и универсальность определения пользовательских функций (расширяет область применения);

2) высокая скорость вычисления (обеспечивает возможность построения интерактивных приложений);

3) контролируемая точность аппроксимации функций (обеспечивает адекватность оценки полученных результатов);

4) минимизация результата аппроксимации (экономит память);

5) взаимодействие с другими системами;

6) универсализация механизма синтеза геометрических моделей.