
Лекция 6
.doc
Предел монотонной последовательности
Теорема Вейерштрасса (о пределе монотонной последовательности). Монотонная ограниченная последовательность сходится.
Доказательство.
►Рассмотрим,
для определенности, неубывающую
последовательность
![]() .
Ограниченное сверху множество значений
последовательности имеет точную верхнюю
грань
.
Ограниченное сверху множество значений
последовательности имеет точную верхнюю
грань
![]() .
Покажем, что число
.
Покажем, что число
![]() будет пределом нашей последовательности.
будет пределом нашей последовательности.
Фиксируем произвольное
![]() .
Из определения точной верхней грани
следует, что существует элемент
последовательности
.
Из определения точной верхней грани
следует, что существует элемент
последовательности
![]() такой, что
такой, что
![]() .
Так как последовательность
.
Так как последовательность
![]() неубывающая, а число
неубывающая, а число
![]() является верхней гранью множества всех
значений последовательности, то для
всех номеров
является верхней гранью множества всех
значений последовательности, то для
всех номеров
![]() будет справедливо
будет справедливо
![]() ,
то есть
,
то есть
![]() .
А это и означает, что
.
А это и означает, что
![]() .◄
.◄
Задача. Доказать, что если
![]() - невозрастающая ограниченная
последовательность, то
- невозрастающая ограниченная
последовательность, то
![]() .
.
Задача. Доказать, что если
![]() -
неубывающая не ограниченная сверху
последовательность, то
-
неубывающая не ограниченная сверху
последовательность, то
![]() .
.
Задача. Доказать, что если
![]() -
невозрастающая не ограниченная снизу
последовательность, то
-
невозрастающая не ограниченная снизу
последовательность, то
![]() .
.
Число е.
Рассмотрим числовую последовательность
![]() . (1)
. (1)
Покажем, что эта последовательность сходящаяся.
Теорема. Последовательность (1) имеет конечный предел.
Доказательство. ►Рассмотрим вспомогательную последовательность
![]() (2)
(2)
и докажем, что она имеет предел. Убедимся сначала, что последовательность (2) убывающая, для этого сравним с 1 отношение
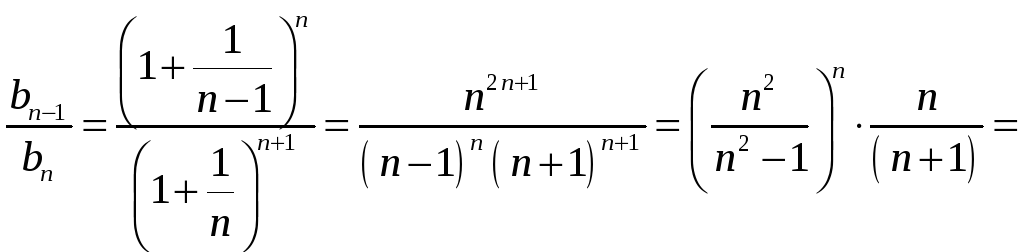
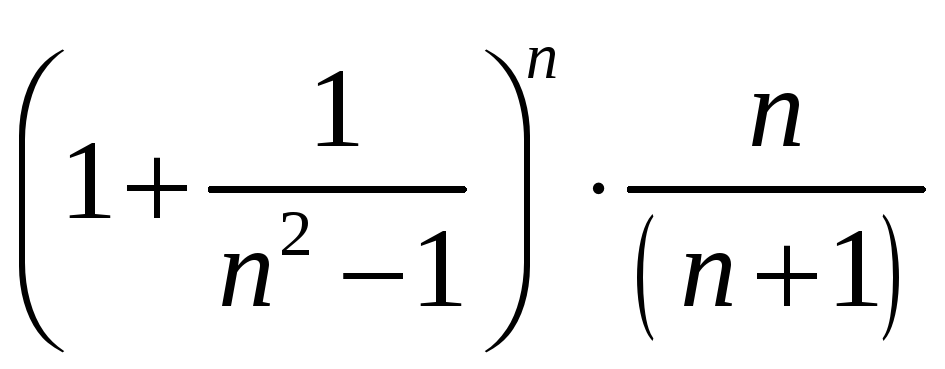 .
.
Далее воспользуемся неравенством Бернулли:
![]() .
.
Последовательность (2) является ограниченной снизу:
![]() .
.
Итак, последовательность
![]() монотонна и ограничена, следовательно,
по теореме Вейерштрасса она имеет
предел. Но тогда имеет предел и
последовательность
монотонна и ограничена, следовательно,
по теореме Вейерштрасса она имеет
предел. Но тогда имеет предел и
последовательность
![]() ,
причем
,
причем
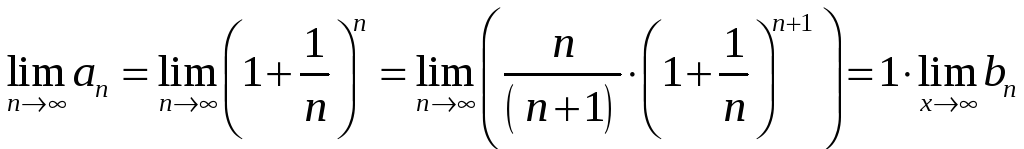 ◄
◄
Пределом последовательности (1) является
число, обозначаемое буквой
![]() ,
оно играет в анализе роль столь же важную
как, например, единица в арифметике или
,
оно играет в анализе роль столь же важную
как, например, единица в арифметике или
![]() в геометрии.
в геометрии.
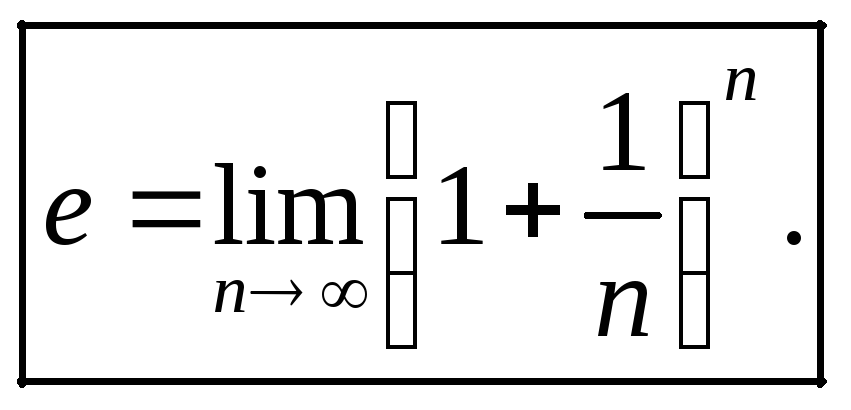
Число
![]() иррациональное, представляется
бесконечной десятичной дробью, а начало
его десятичного разложения имеет вид:
иррациональное, представляется
бесконечной десятичной дробью, а начало
его десятичного разложения имеет вид:
![]()
Задача.
Доказать, что
![]() .
.
Второй замечательный предел
Теорема. Справедливо равенство
![]() .
(1)
.
(1)
Доказательство. 4Сначала покажем, что
![]() .
(2)
.
(2)
Заметим, что при
![]() будет выполнено
будет выполнено
![]() ,
откуда, используя монотонность
показательной (
,
откуда, используя монотонность
показательной (![]() при
при
![]() возрастает) и степенной (
возрастает) и степенной (![]() возрастает при
возрастает при
![]() и
и
![]() )
функций, получим
)
функций, получим
![]() (3)
(3)
Положим
![]() и
и
![]() .
Имеем
.
Имеем
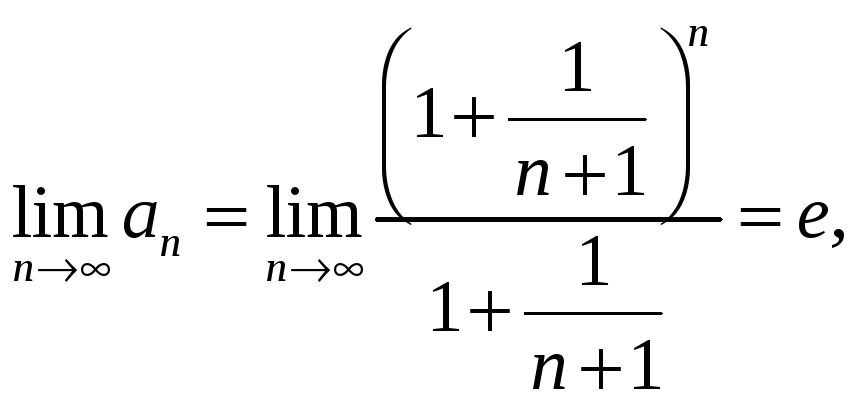 (4)
(4)
![]() (5)
(5)
Фиксируем произвольное
![]() .
Из (4) и (5) следует, что существует такое
.
Из (4) и (5) следует, что существует такое
![]() ,
что при
,
что при
![]() будет справедливо
будет справедливо
![]() и
и
![]() (6)
(6)
Возьмем
![]() и положим
и положим
![]() .
Тогда будет
.
Тогда будет
![]() ,
и в силу (3) и (6) имеем
,
и в силу (3) и (6) имеем
![]() то есть
то есть
![]()
Формула (2) доказана.
Пусть теперь
![]() .
Тогда
.
Тогда
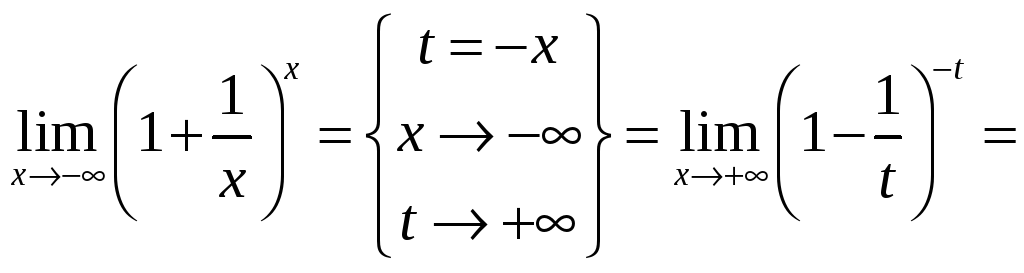
![]()
![]()
то есть
![]() .3
.3
Следствие.
![]()
Доказательство. 4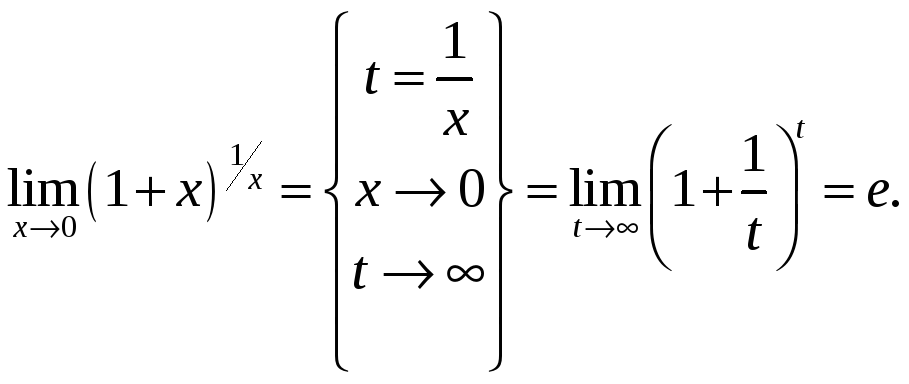 3
3
Непрерывность
Определение. Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
![]() .
Говорят, что функция
.
Говорят, что функция
![]() непрерывна в
непрерывна в
![]() ,
если существует предел
,
если существует предел
![]() при
при
![]() ,
равный
,
равный
![]() :
:
![]() .
.
Запишем это определение с кванторами:
![]() ,
,
или в неравенствах:
![]() .
.
Определение. Если функция
![]() непрерывна в любой точке
непрерывна в любой точке
![]() ,
то говорят, что она непрерывна на этом
интервале.
,
то говорят, что она непрерывна на этом
интервале.
Если функция
![]() не является непрерывной в точке
не является непрерывной в точке
![]() ,
то
,
то
![]() называется точкой разрыва
называется точкой разрыва
![]() и говорят, что
и говорят, что
![]() разрывна в
разрывна в
![]() .
.
Задача. Докажите, что функция
![]() непрерывна на всей оси.
непрерывна на всей оси.
Утверждение.
Основные элементарные функции
![]() непрерывны на своей области определения.
непрерывны на своей области определения.
(без доказательства)
Что касается свойств непрерывных
функций, то ограниченность непрерывной
функции в окрестности точки
![]() ,
непрерывность линейной комбинации,
произведения и частного (при условии
отличия от нуля знаменателя в точке
,
непрерывность линейной комбинации,
произведения и частного (при условии
отличия от нуля знаменателя в точке
![]() )
двух непрерывных функций являются
тривиальными следствиями соответствующих
свойств предела функции.
)
двух непрерывных функций являются
тривиальными следствиями соответствующих
свойств предела функции.
Для примера докажем утверждение о непрерывности суммы непрерывных функций.
Утверждение. Пусть функции
![]() и
и
![]() непрерывны в точке
непрерывны в точке
![]() .
Тогда их сумма
.
Тогда их сумма
![]() также будет непрерывной в точке
также будет непрерывной в точке
![]() .
.
Доказательство.
![]() Имеем
Имеем
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.![]()
Докажем вариант теоремы о предельном переходе в неравенстве для непрерывных функций.
Теорема (о сохранении знака
непрерывной функцией). Пусть функция
![]() непрерывна в точке
непрерывна в точке
![]() и пусть
и пусть
![]() .
Тогда
.
Тогда
![]() сохраняет знак в некоторой окрестности
точки
сохраняет знак в некоторой окрестности
точки
![]() .
.
Доказательство. 4Непрерывность
функции
![]() означает, что
означает, что
![]() .
Тогда по лемме о сохранении функцией
знака своего предела в некоторой
проколотой окрестности точки
.
Тогда по лемме о сохранении функцией
знака своего предела в некоторой
проколотой окрестности точки
![]() функция сохраняет знак
функция сохраняет знак
![]() ,
то есть во всей этой окрестности не
меняет знак.3
,
то есть во всей этой окрестности не
меняет знак.3
Упражнение. Пользуясь теоремами об арифметических действиях с пределами функций сформулируйте и докажите теорему о непрерывности линейной комбинации непрерывных функций, теоремы о непрерывности произведения и частного.
Теорема (о пределе сложной
функции). Пусть функция
![]() ,
определенная в проколотой окрестности
,
определенная в проколотой окрестности
![]() точки
точки
![]() ,
имеет предел
,
имеет предел
![]() при
при
![]() :
:
![]() . (1)
. (1)
И пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
![]() ,
содержащей
,
содержащей
![]() ,
и непрерывна в точке
,
и непрерывна в точке
![]() .
.
Тогда сложная функция
![]() определена в
определена в
![]() и существует предел
и существует предел
![]() .
(2)
.
(2)
(Другими словами,
![]() ).
).
Доказательство. 4Фиксируем
произвольное
![]() .
Из непрерывности функции
.
Из непрерывности функции
![]() в точке
в точке
![]() следует
следует
![]() , (3)
, (3)
а из существования предела (1), что
![]() . (4)
. (4)
Объединяя (3) и (4), получим
![]() .
.
Существование предела (2) доказано. 3
Следствие.
Пусть функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
а функция
,
а функция
![]() непрерывна в точке
непрерывна в точке
![]() .
Тогда сложная функция
.
Тогда сложная функция
![]() будет непрерывной в точке
будет непрерывной в точке
![]() .
.
Утверждение.
![]()
Доказательство. 4
![]() 3
3
Утверждение.
![]()
Доказательство. 4
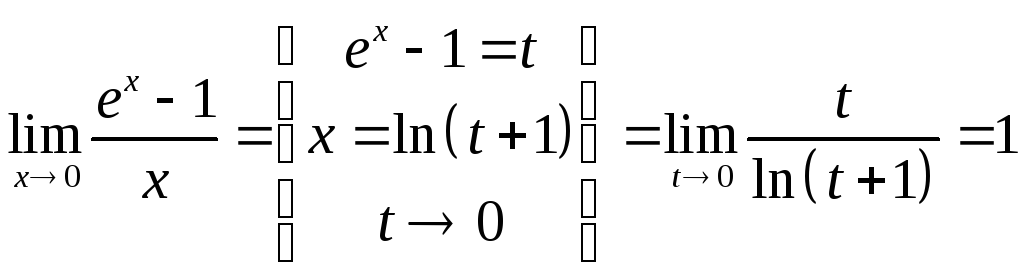 .3
.3
Примечание. Последние две формулы можно записать в следующем виде:
![]()
![]() или
или
![]()
Замечание. Пусть непрерывные
в нуле функции
![]() и
и
![]() эквивалентны при
эквивалентны при
![]() ,
а функция
,
а функция
![]() бесконечно малая при
бесконечно малая при
![]() .
.
Тогда функция
![]() будет эквивалентна функции
будет эквивалентна функции
![]() при
при
![]() .
.
Доказательство. ► В самом деле,
эквивалентность функций
![]() и
и
![]() означает, что
означает, что
![]() ,
(5)
,
(5)
где
![]() - бесконечно малая функция при
- бесконечно малая функция при
![]() .
Доопределим
.
Доопределим
![]() в нуле, положив
в нуле, положив
![]() .
Равенство (5) не изменится, а функция
.
Равенство (5) не изменится, а функция
![]() будет в нуле непрерывной. Сделаем замену
переменной
будет в нуле непрерывной. Сделаем замену
переменной
![]() ,
получим
,
получим
![]() ,
,
где
![]() в силу теоремы о пределе сложной функции.
◄
в силу теоремы о пределе сложной функции.
◄
Последнее замечание позволяет нам упрощать выкладки при вычислении пределов.
Утверждение.
![]()
Доказательство:
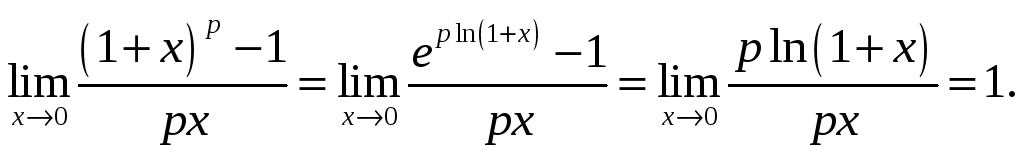
То есть мы можем записать:
![]() или
или
![]()
