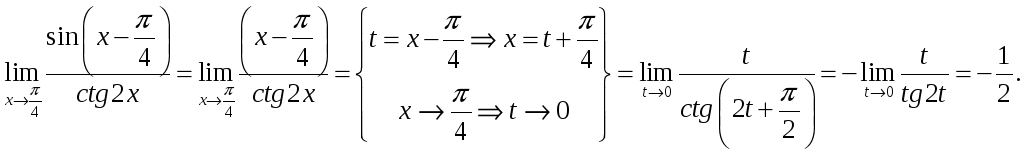Лекция 5

27

Переход к пределу в неравенствах

Теорема (о предельном переходе в неравенстве). Пусть и , и пусть , по крайней мере, начиная с некоторого номера . Тогда .

Доказательство. ►Рассмотрим последовательность . Эта последовательность сходящаяся , кроме того, при . Покажем, что .

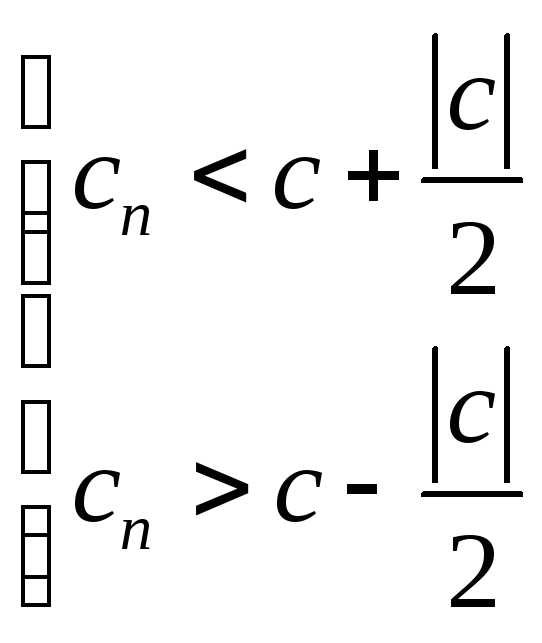
Предположим, что . Тогда возьмем и выберем номер такой, что при

, то есть .

Но в таком случае, при будет (мы используем только верхнее неравенство) . Мы пришли к противоречию. следовательно .◄

Теорема (о предельном переходе в двух неравенствах). Пусть и , и пусть , по крайней мере, начиная с некоторого номера .

Тогда последовательность сходится и .

Доказательство. ►Фиксируем произвольное . По условию теоремы, после некоторого номера , элементы последовательности будут находиться в , а, после номера , в той же окрестности будут находиться все члены последовательности . Тогда для номеров элемент последовательности , находясь между и , тоже попадет в , то есть .◄

Теперь докажем аналогичные теоремы для функций.

Теорема (о переходе к пределу в неравенстве). Пусть функции определены в некоторой проколотой окрестности точки - , и пусть в этой окрестности выполнено неравенство , а также существуют пределы и . Тогда .

Доказательство. 4Из определения предела по Гейне следует, что для любой последовательности такой, что и будет справедливо и . Кроме того, с некоторого номера (когда члены последовательности попадут в ) будет выполняться неравенство . Применив теорему о предельном переходе в неравенстве к последовательностям и , получим нужное нам неравенство . 3

Теорема (о переходе к пределу в двух неравенствах). Пусть функции определены в некоторой проколотой окрестности точки - , и пусть в этой окрестности выполнено неравенство , а также существуют и равны пределы . Тогда существует предел .

Доказательство. 4Из условий теоремы следует, что для любой последовательности такой, что и будет справедливо , а также, что с некоторого номера (когда члены последовательности попадут в ) будет выполняться неравенство . Применим теорему о предельном переходе в двух неравенствах к последовательностям . Получим существование предела для любой последовательности , сходящейся к (). Следовательно, для функции в выполнены все условия существования предела по Гейне. 3

Лемма (о сохранении знака). Пусть существует . Тогда в некоторой проколотой окрестности точки знаки функции и ее предела будут совпадать .

Доказательство. 4Предположим для определенности, что . Положим . Из существования предела при стремлении к точке следует, что существует проколотая окрестность , в которой выполнено неравенство . Тогда для будет верно

.3

Первый замечательный предел

Теорема (о первом замечательном пределе). Справедлива формула

.

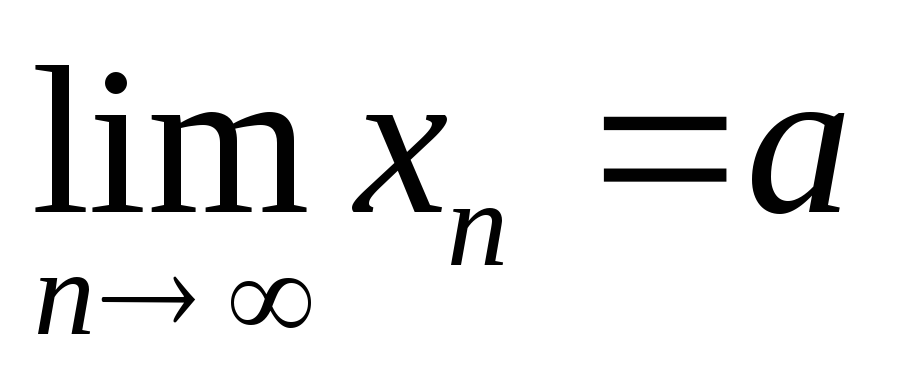Доказательство. Мы будем использовать школьное определение как ординаты конца единичного вектора при повороте его (с центром в начале координат) на угол радиан. Так как нас интересует случай , то можно считать, что , а поскольку функция четная, то достаточно рассмотреть углы из первой четверти: .

Из геометрических соображений ясно, что площадь кругового сектора больше площади треугольника и меньше площади треугольника :

,

то есть

или .

Так как

,

то по теореме о предельном переходе в двух неравенствах получим

.

Сравнение асимптотического поведения функций

Иногда возникает вопрос об описании поведения функции вблизи некоторой точки (или бесконечности), в которой часто сама функция не определена. Тогда говорят, что интересуются асимптотикой или асимптотическим поведением функции в окрестности этой точки. При этом поведение функции сравнивают с поведением другой, более простой или более изученной функции, которая в окрестности данной точки приближает исследуемую функцию с малой относительной погрешностью.

Дадим определение некоторых элементарных понятий, относящихся к асимптотическому поведению функций.

Определение. Говорят, что функция есть бесконечно малая по сравнению с функцией при и пишут , если , где - бесконечно малая функция при .

Замечание. Если функция в , то последнее определение можно записать как

.

Пример 1. при .

Пример 2. при .

Определение. Запись

означает, что

,

где - ограниченная функция в некоторой окрестности или проколотой окрестности .

Замечание. Если в (в ), то

, когда функция будет ограниченной в этой окрестности.

Пример. . В самом деле, (при и ) имеем 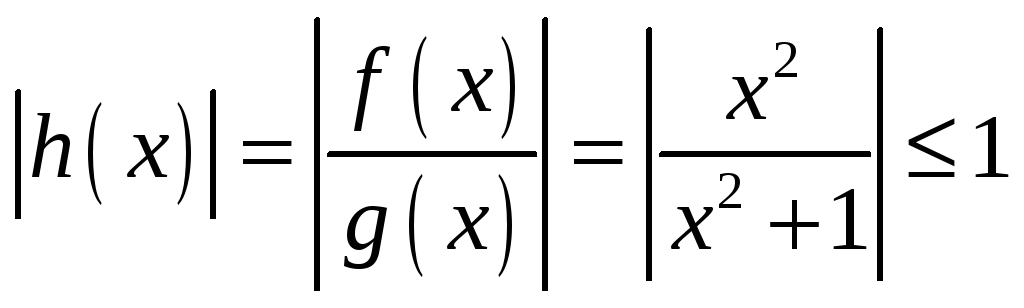на всей оси.

Определение. Говорят, что функции и эквивалентны при и пишут , если , где - бесконечно малая функция при .

Если мы раскроем скобки в правой части равенства, то получим еще один вариант определения:

Замечание. Если в некоторой , то

.

Пример. (первый замечательный предел);

Задача. Докажите, что

.

Утверждение. Соотношение обладает всеми свойствами эквивалентности:

а так как то ( - б.м. при ), то и .

, а так как то где - б.м. при .

Утверждение. Если и , то .

Доказательство.►.

Разумеется, мы предполагаем здесь, что знаменатели всех дробей в некоторой окрестности точки отличны от нуля.◄

Задача. Доказать, что Если и , то .

Замечание. Нельзя утверждать, что если и , то . Примером может послужить пара и при . Так как

при , но, очевидно, .

Замечание. Пусть непрерывные в нуле функции и эквивалентны при , а функция бесконечно малая при .

Тогда функция будет эквивалентна функции при .

Доказательство будет приведено позднее.

Последнее замечание позволяет нам упрощать выкладки при вычислении пределов.

Пример.