
- •Лекция 1. Базы данных в системе экономической информации Основные понятия
- •1.1 Роль и место баз данных в системе экономической информации
- •1.2 Базы данных: основные понятия
- •Лекция 2. Предметная область и ее структура
- •2.1 Предметная область: основные понятия
- •2.2 Исчисление типов отношений между типами объектов
- •2.3 Модель «сущность-связь» и ее разновидности. Основы er моделирования
- •2.4 Структурирование предметной области с позиций функций и задач управления
- •2.5 Матрица отношений между типами объектов
- •Лекция 3. Реляционные базы данных
- •3.1 Отношения реляционных баз данных и свойства
- •3.2 Достоинства и недостатки реляционных баз данных
- •3.3 Элементы реляционной алгебры, реляционного исчисления и трехзначной логики
- •Естественное соединение
- •Правила трехзначной логики
- •Лекция 4. Нормализация таблиц реляционных баз данных
- •4.1 Принципы нормализации
- •4.2 Нормальные формы
- •Лекция 5. Проектирование и создание запросов. Структурированный язык запросов (sql).
- •5.1 Понятие запроса
- •5.2 Соединение таблиц в запросах
- •5.3 Соединение трех и более таблиц
- •5.4 Запрос на выборку
- •5.5 Запрос на выборку с группировкой
- •5.6 Перекрестный запрос
- •5.7 Перекрестный запрос с составным заголовком строк
- •5.8 Запрос на обновление
- •5.9 Запрос на удаление
- •5.10 Запрос на добавление
- •5.11 Логически выраженные команды sql
- •Лекция 6. Microsoft Access как объективно-ориентированная система
- •6.1 Понятие события.
- •6.2 Понятие объектов, их свойств и методов
- •Лекция 7. Современные тенденции развития бд
- •7.2 Основные концепции объектно-ориентированного подхода
3.2 Достоинства и недостатки реляционных баз данных
К достоинствам реляционных СУБД можно отнести:
-
Наличие развитой теории реляционной модели данных. Реляционная модель данных поддерживается в большей степени, чем другие модели. Для манипулирования отношениями используются элементы реляционной алгебры.
-
Возможность и наличие аппарата сведения других моделей данных к реляционной.
-
Поддержка реляционной модели специальных средств ускоренного доступа к данным. Имеются прежде всего индексирование и кэширование.
-
Возможность манипуляции данными без необходимости знаний физической организации базы данных.
-
Наличие стандартизированного высокоуровневого языка запросов SQL (STRUCTURED, QUERY LANGVAGE).
-
Простота использования реляционной модели данных.
Благодаря своим достоинствам реляционная модель данных получила широкое распространение в таких традиционных бизнес приложениях, как: обработка заказов, учет складских запасов, банковское дело, заказ авиабилетов, бухгалтерский учет и т.д.
Вместе с тем реляционные модели баз данных имеют и ряд недостатков. Прежде всего реляционные базы данных показали свою неадекватность в следующих типах приложених: CAD (computer-aided design), CAM (computer-aided manufacturing), CASE (software engineering), офисных и мультимедиа-приложениях, цифровом издательском деле, геоинформационных системах, научных и исследовательских приложениях и экспериментальных системах.
Среди других недостатков реляционных СУБД сторонники объективно-ориентированного программирования отмечают:
-
слабое представление сущностей реального мира;
-
семантическая перегрузка;
-
слабая поддержка ограничения целостности и корпоративных ограничений;
-
однородная структура данных;
-
ограниченный набор операций;
-
трудности организации рекурсивных запросов и т.д.
3.3 Элементы реляционной алгебры, реляционного исчисления и трехзначной логики
Формальной основой реляционной модели данных является реляционная алгебра, основанная на теории множеств и рассматривающая специальные операции над отношениями, и реляционное исчисление, базирующее на математической логике.
Вариант реляционной алгебры, предложенный доктором Коддом, состоит из восьми операций, в том числе пяти основных и трех дополнительных.
-
Выборка отношений. (Selection) предикат(R).
Операция выборки работает с одним отношением R и определяет результирующее отношение, которое содержит только те кортежи отношения R, которые удовлетворяют заданному условию (предикату). Сложные предикаты могут быть созданы с помощью логических операторов and, or и not.
Например, из табл. “Сотрудники” требуется выбрать тех, кто родился ранее 01.01.78.
|
Таблица 3.3.1 |
||
|
Сотрудники
|
||
|
КодСотр |
ФамСотр |
ДатаРожд |
|
001 |
Иванов |
05/08/74 |
|
002 |
Петров |
19/06/69 |
|
003 |
Сидоров |
20/01/79 |
δ ДатаРожд ≥01/01/78(Сотрудники)
Результирующая таблица будет выглядеть следующим образом:
|
Таблица 3.3.2 |
||
|
Сотрудники
|
||
|
КодСотр |
КодСотр |
КодСотр |
|
003 |
003 |
003 |
-
Проекция отношения. (Projection) Патр.1,…, атр.n (R).
Операция проекции обозначается Патр. Работает с одним отношением R и определяет новое отношение, содержащее вертикальное подмножество отношения R, создаваемое посредством извлечения значений, указанных атрибутов и исключением из результатов строк – дубликатов.
Например: П КодСотр,ФамСотр (Сотрудники). Результирующая таблица будет выглядеть следующим образом:
|
Таблица 3.3.3 |
|
|
Сотрудники
|
|
|
КодСотр |
ФамСотр |
|
001 |
Иванов |
|
002 |
Петров |
|
003 |
Сидоров |
|
Таблица 3.3.4 |
||
|
Путевки
|
||
|
КодКл |
ФамКл |
Стр |
|
001 |
Иванов |
Франция |
|
002 |
Петров |
Италия |
|
003 |
Сидоров |
Испания |
|
003 |
Сидоров |
Германия |
|
002 |
Петров |
Испания |
П КодКл,ФамКл (Путевки). Результирующая таблица примет вид:
|
Таблица 3.3.5 |
|
|
|
|
|
КодКл |
ФамКл |
|
001 |
Иванов |
|
002 |
Петров |
|
003 |
Сидоров |
-
Объединение отношений (Union) RUS.
Объединение отношений R и S с кортежами i и j соответственно можно получить в результате их конкатенации с образованием одного отношения с максимальным количеством кортежей i+j. Кортежи – дубликаты из результатов операции исключаются. При этом отношения R и S должны быть совместимы по объединению (т.е. они должны иметь одинаковое количество атрибутов с совпадающим доменом).
|
Таблица 3.3.6 |
|
Таблица 3.3.7 |
||
|
Студенты
|
|
Преподаватели |
||
|
КодСт |
ФамСт |
|
КодПреп |
ФамПреп |
|
С001 |
Сидоров |
|
П001 |
Бондарев |
|
С002 |
Петров |
|
П002 |
Лосев |
|
С003 |
Иванов |
|
|
|
|
Таблица 3.3.8 |
|
|
(Студенты)
|
|
|
Код |
Фам |
|
С001 |
Сидоров |
|
С002 |
Петров |
|
С003 |
Иванов |
|
П001 |
Бондарев |
|
П002 |
Лосев |
-
Произведение отношений (Cartesian product) RxS.
Операция декартового произведения определяет новое отношение, которое является результатом конкатенации (сцепления) каждого кортежа из отношения R с каждым кортежем из отношения S.
|
Таблица 3.3.9 |
|||
|
(Преподаватели)×(Студенты)
|
|||
|
КодПреп |
ФамПреп |
КодСт |
ФамСт |
|
П001 |
Бондарев |
С001 |
Сидоров |
|
П001 |
Бондарев |
С002 |
Петров |
|
П001 |
Бондарев |
С003 |
Иванов |
|
П002 |
Лосев |
С001 |
Сидоров |
|
П002 |
Лосев |
С002 |
Петров |
|
П002 |
Лосев |
С003 |
Иванов |
-
Разность отношений (Set difference) R-S.
Разность отношений состоит из кортежей, которые имеются в отношение R, но отсутствуют в отношении S, причем отношения R и S должны быть совместимы по объединению.
|
Таблица 3.3.10 |
|
Таблица 3.3.11 |
|||
|
Студенты “5”
|
|
Студенты “4” |
|||
|
КодСт |
ФамСт |
|
КодСт |
ФамСт |
|
|
С001 |
Сидоров |
|
С001 |
Сидоров |
|
|
С002 |
Петров |
|
С003 |
Иванов |
|
|
С003 |
Иванов |
|
|
|
|
|
Таблица 3.3.12 |
|
|
Студенты “5” - Студенты “4”
|
|
|
КодСт |
ФамСт |
|
С002 |
Петров |
Операции 1-5 являются основными.
-
Пересечение отношений (Intersection) RS : RS = R-(R-S).
Операция пересечения определяет отношение, которое содержит кортежи, присутствующие как в отношении R, так и в отношении S. Отношения R и S должны быть совместимы по объединению. Пересечение может быть сформулировано и на операции разности множеств.
|
Таблица 3.3.13 |
|
Таблица 3.3.14 |
|||
|
Студенты “5”
|
|
Студенты “4” |
|||
|
КодСт |
ФамСт |
|
КодСт |
ФамСт |
|
|
С001 |
Сидоров |
|
С001 |
Сидоров |
|
|
С002 |
Петров |
|
С003 |
Иванов |
|
|
С003 |
Иванов |
|
C004 |
Яковлев |
|
|
|
|
|
C005 |
Лесков |
|
|
Таблица 3.3.15 |
|
|
Студенты “5”
|
|
|
КодСт |
ФамСт |
|
С003 |
Иванов |
|
С001 |
Сидоров |
-
Соединение отношений (Join).
Существует несколько типов операций соединения:
-
– соединение (тета-соединение);
-
соединение по эквивалентности (equi-jоin);
-
естественное соединения (natural join);
-
внешнее соединение;
-
полусоединение (outer join).
Деление (Division) R÷S. Т1 = Пс(R), Т2 = Пс((SxT1)-R); T=T1- T2
Результатом операции деления является набор кортежей отношения R, определенных на множестве атрибутов С, которые соответствует комбинации всех кортежей отношения S.
Представим схематически операции реляционной алгебры

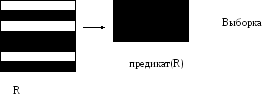

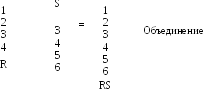


Операция «тета»-соединения (). Определенное отношение в котором содержится кортеж из декартового произведения отношения R и S, удовлетворяющее предикату.
Предикат F имеет вид R ai S bi, где вместо может быть указан один из операторов сравнения <, >, , , =, . ai и bi – это атрибуты отношений R и S соответственно. Отношения -соединения можно переписать на основе базовых операций выборки и декартового соединения.


Соединение по эквивалентности
Если предикат F содержит только операторы равенства, то соединение называется соединением по эквивалентности.

 (Преподаватели)
(Преподаватели)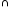 Студенты “4”
Студенты “4”