2. Интерполирование функций

1. Общие положения

Необходимо определить значения функции при некоторых частных значениях независимого переменного , находящегося в интервале . Аналитическое выражение неизвестно. – точки, в которых известны значения функции: , т.е. существует ряд точек , лежащих на кривой (рис. 5.1).

Другими словами, на отрезке заданы узлов интерполяции , а также значения функции в этих точках:

.

Требуется построить непрерывную (интерполирующую) функцию , принимающую в узлах интерполяции те же значения, что и , т.е. такую, что

.

2. Интерполяционная формула Лагранжа

Если на отрезке даны различных значений аргумента и для функции известны значения:

,

то приближенное значение функции на отрезке определяют с помощью интерполяционной формулы Лагранжа

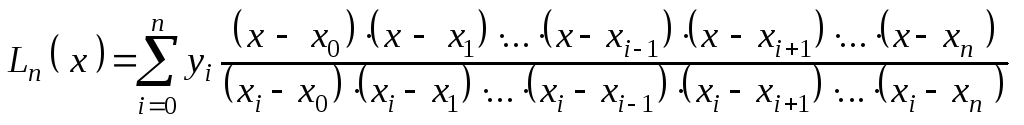
1.2.3 Сплайн-интерполяция

Кубическая сплайн-интерполяция означает, что между любыми соседними узлами

функция интерполируется кубическим полиномом, равным значению функции в каждом узле и во всех узлах непрерывны его первая и вторая производные (условия сопряжения).

Кубический полином

интерполирует функцию на интервале , а

(5.7)

на интервале .

1.2.4 Полученные решения

ans =

Точное значение функции в точке 0.4975710 , по формуле Лагранжа 0.4975864 , погрешность 0.0000154

ans =

Точное значение функции в точке 0.4975710 , применяя кусочно-линейное интерполирование 0.4877625 , погрешность 0.0098085

ans =

Точное значение функции в точке 0.4975710 , применяя кусочно-квадратичное интерполирование -0.4559234 , погрешность 0.9534945

ans =

Точное значение функции в точке 0.4975710 , применяя интерполирование сплайнами 0.5551660 , погрешность 0.0575950

3. Решение обыкновенных дифференциальных уравнений

1.3.1 Общие положения

Пусть на отрезке требуется найти функцию , удовлетворяющую уравнению

и начальному условию

.

Здесь – заданная непрерывная функция заданных аргументов.

Решить приведенную задачу численно – это значит для заданной последовательности чисел из отрезка и числа , не находя самого решения , вычислить (приближенно) значения этого решения в точках .

В этом случае можно искомую интегральную функцию заменить ломаной, вершинами которой являются точки при условии, что направление отрезка совпадает с направлением интегральной кривой в точке . Иначе говоря, необходимо, чтобы

,

Следует:

.

1.3.2. Модификации метода Эйлера

Более точным является усовершенствованный метод Эйлера, когда сначала вычисляют промежуточные значения

, ,

а потом значения:

.

Другой модификацией метода Эйлера является усовершенствованный метод Эйлера-Коши. Его сущность заключается в следующем: сначала выбирают «грубое» приближение к решению – затем, исходя и данного выражения, вычисляют а потом приближенно полагают, что

.

Усовершенствованный метод Эйлера можно еще более уточнить, применив итерационную обработку каждого значения . Исходя из «грубого» приближения строят итерационный процесс вида:

, .

Процесс итерации продолжают до тех пор, пока два последующих приближения и не будут совпадать в соответствующих десятичных знаках. После этого полагают – общая часть приближений и .

Метод Эйлера с итерационной обработкой дает на каждом шагу погрешность порядка и нередко используется в вычислительной практике.

1.3.3. Метод Рунге-Кутты

Метод Рунге-Кутты характеризуется повышенной точности и принадлежит к многошаговым методам численного интегрирования задачи Коши

.

Пусть – шаг интегрирования. Вычисление приближенного значения при решении задачи Коши в точке методом Рунге-Кутты заключается в выполнении операций, связанных с определением на каждом ом шаге коэффициентов

и далее значений

1.3.4 Полученные решения

Графики зависимостей:

Решение в общем виде:

4. Одномерная оптимизация

1. Общие сведения

Пусть функция определена на . Задачей одномерной оптимизации называют задачу, в которой требуется найти

.

Решением или точкой максимума (минимума) задачи называют точку такую, что

для всех .

Для нахождения интервала, на котором функция имеет экстремум, воспользуемся алгоритмом Свенна.

Алгоритм Свенна

Исходные данные: х₀ – начальная точка, h – шаг поиска (h>0).

Шаг 1. Вычислить f(x₀); f(x₀ +h); f(x₀ -h); k=1.

Шаг 2. Если f(x₀ -h) ≤ f(x₀) ≤ f(x₀ +h), то x₁ = x₀ + h, перейти к шагу 4.

Шаг 3. Если f(x₀ -h) ≥ f(x₀) ≥ f(x₀ +h), то х₁ = x₀ - h, h = -h, перейти к шагу 4, в противном случае (f(x₀ -h) ≤ f(x₀) ≥ f(x₀ +h)), a = x₀ – h; b = x₀ + h, конец.

Шаг 4. x_k+1 = x_k + 2^kh , вычислить f(x_k+1).

Шаг 5. Если f(x_k+1 ) ≥ f(x_k ), то к = к + 1, перейти к шагу 4.

Шаг 6. Если h > 0, то a = x_k-1 , b = x_k+1, конец, в противном случае a = x_k+1 , b = x_k-1 , конец.

Случай f(x₀ -h) ≥ f(x₀) ≤ f(x₀ +h) (шаг 3) не рассматривается, т.к. он противоречит предположению об унимодальности функции f(x).

Для нахождения экстремума воспользуемся методом Ньютона.

Алгоритм

1. Задается начальное приближение x0.

2. Пока не выполнено условие остановки, в качестве которого можно взять 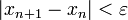  или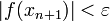  (то есть погрешность в нужных пределах), вычисляют новое приближение:  .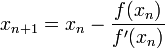

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Условия применимости накладывает теорема Канторовича:

Пусть задано уравнени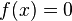е  , где   и надо найти его решение.

Тогда ограничения на исходную функцию 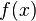  будут выглядеть так:

1. функция должна быть ограничена;

2. функция должна быть гладкой, дважды дифференцируемой;

3. её первая производная 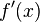  равномерно отделена от нуля;

4. её вторая производная 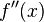  должна быть равномерно ограничена.