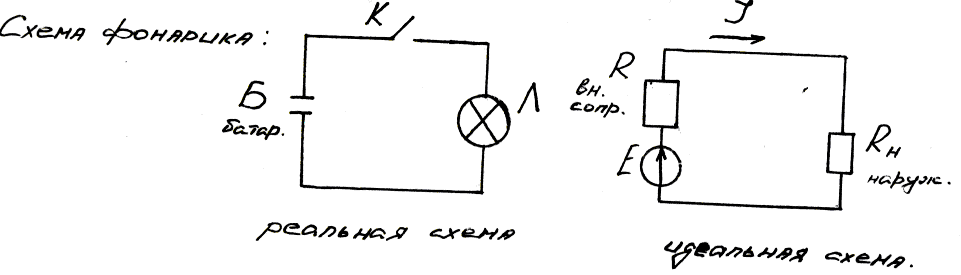
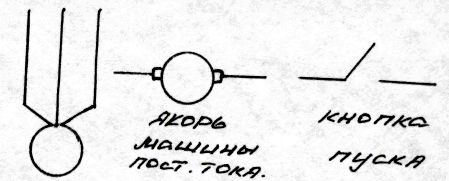
1. Элементы электрических цепей и схем.Классификация электрический цепей Электротехника-наука о производстве, передаче и практическом использовании электрической энергии. Электрическая цепь-совокупность устройств, кот-ые предназначены для производства, передачи и распределения эл. энергии. Процессы, протекающие в электрич-их устройствах, описываются током (J), напряжением(U) и электродвижущей силой (Е-ЭДС). Электрические цепи делятся: 1) цепи постоянного тока-эл. цепь, в кот-ой преобразование энергии происходит при постоянных токах и напряжениях. 2) цепи переменного тока- эл. цепь, в кот-ой преобразование энергии происходит при изменяющихся величинах токов и напряжений. Основными элементами эл. цепи явл. : источники, приемники, линии электропередач. В источниках энергия дугих видов преобр-ся (механич-ая, ядерная, химич-ая) в электрич-ую энергию. В приемниках происходит потребление энергии. Электрич-ая схема-графическое изображение цепи при помощи условных обозначений:

Для облегчения анализа процессов, происходящих в эл. цепи, ее заменяют схемой замещения. В схемах замещения реальные элементы заменяются идеальными. Матем-ие описания процессов в идеальных элементах отображают главные процессы, происходящие в реальной цепи. Идеальн. элемент бывает: 1) идеальный источник ЭДС

хар-ет спос-ть источника создавать опред-ю разность потенциалов (φ)

2) ид. источник тока, еденица измер. [А]

3) идеально-резистивный элемент хар-ет необратимый процесс преобр-ия эл-кой энергии в тепловую, [Ом]

4) ид. емкостной элемент хар-ет спос-ть эл-та создавать эл. поле.

5) ид. индуктивный элемент хар-ет спос-ть эл-та создавать магн-е поле, [Гн]

Первые 3 элемента используется только в цепях пост. тока, все 5 эл-тов использ-ся как в цепях постоянного тока, так и в цепях переменного тока. Пример: реальная катушка индуктивности

заменяется в цепи постоянного тока.

заменяется

в цепи переменного тока

Электрич-ие цепи бывают: 1) линейные (когда все эл-ты обл-т линейными хар-ами), 2) нелинейные (когда все ее элементы обл-т нелин-ыми хар-ми). Вольтамперная хар-ка:

2. Метод контурных токов. Метод непосредственного применения з-нов Кирхгофа . Методы контурных токов позволяет сократить кол-во ур-ний. Ур-ния сост-ся по 2-му з-ну Кирхгофа. Направление контурных токов выб-ся произвольно, но их желательно напр-ть в одну сторону.

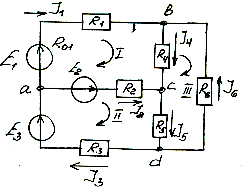
Решение: 1) выбираем напр. конт-ых токов; 2) сост-ся ур-ния по методу токов:

J_k1(R₁+R₄+R₂+R₀₂+R₀₁)-J_k2(R₂=R₀₂)-J_k3R₄=E₁-E₂

J_k2(R₀₂+R₂+R₅+R₃)-J_k1(R₀₂+R₂)-J_k3R₅=E₃+E₂

J_k3(R₄+R₅+R₆)-J_k1R₄-J_k2R₅=0 J_k1, J_k2, J_k3.

Произ-но выбираем напр. токов J1=Jk1 J2=Jk1-Jk1 J3=Jk3 J4=Jk1-Jk3 J5=Jk2-Jk3 J6=Jk3

Метод непосредственного применения з-нов Кирхгофа . Применим для расчета любой по сложности разветвленной цепи с несколькими источниками питания. Сущность: в составлении и решении уравнений относительно неизвестных токов. При этом по 1-ому з-ну Кирхгофа составл-ся узел “минус” 1-ое ур-ние. Кол-во ур-ний = кол-ву ветвей в системе. Остальные ветви “минус” (узел-1 ур-ие) составляются по 2-ому з-ну Кирхгофа. 6-(у-1)=кол-ву независимых контуров. Независимый контур-контур, содержащий хотя бы одну ветвь, не входящий в другие контуры. Пример: Дано: R₀₃=0, R₁R₂R₃R₄R₅=R₆, R₀₁R₀₂R₀₃=0, E₁E₂E₃ Найти: J₁,J₂,J₃,J₄,J₅,J₆.

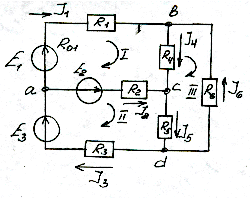
Решение: 1) определим кол-во ветвей и кол-во узлов в системе (узлы a, b, c, d y=4; ветвей 6 b=6); 2) произвольно выбираем направление токов в ветвях и указываем их на схеме; 3) составляем узел-1-ур-ние у-1=3 (1 з-н Кирхгофа) узел а: -J₁-J₂+J₃=0; узел b: J₁-J₄+J₆=0; узел c: J₄+J₂-J₅=0; 4) выбираем ветвь В-(у-1)=3 (2 з-н Кирхгофа).

3 независимых контура: J₁(R₁+R₀₁)+J₄R₄-J₂(R₂+R₀₂=E₁-E₂)

J₂(R₂+R₀₂)+J₅R₅+J₃R₃=E₂+E₃

-J₄R₄-J₅R₅-J₆R₆=0

Если в рез-те расчета некоторые токи получились отриц., то действит-ое значение тока противоположное.

3.Метод измерения напряжений м/у 2-мя узлами (метод 2-ух узлов) исп-ся для расчета разветвленных цепей с неск-ми источ-ми ЭДС, все ветви кот. присоед. к 2-ум узлам.

J₁=(E₁-Uab)g₁; J₂=-Uab∙g₂; J₃=(-E₃-Uab);. Jn=(En-Uab)g_n. J₁+J₂+J₃…+Jn=E₁g₁-Uab∙g₁-Uab∙ g₂+E₃g₃-Uab∙g₃+En∙g_n-Uab∙g_n ; 0=E₁g₁-E₃g₃+Eng_n-Uab(g₁+g₂+g₃+…+g_n). Uab=(E₁g₁-E₃g₃+…+Eng_n)/(g₁+g₂+g₃+…+g_n), след-но,( ±ΣEig₁)/Σg₁=Uab - ф-ла напряж. 2-ух узлов. Напр. м/у 2-мя узлами = дроби, в числителе кот-ой стоит алгебраич-ая сумма ЭДС провод-ти, а в знаменателе стоит сумма ЭДС умноженное на проводимости ветвей, в заменателе стоит алгебраическая сумма проводимости всех ветвей.. Примечание: если в какой-либо ветви U отсут-ет, то слагаемое Eg для этой ветви не будет, но взамен пров-ть этой ветви ост-ся.

4.Баланс мощностей в элект.цепях.Основные законы электр.цепей постоянного тока. З-н Ома: J=U/R, U=JR. Участок эл. цепи с несколькими послед-но соед-ми резистивными элементами и источниками ЭДС

Пусть величина потенциала (∙) 1-φ₁; (∙) 2-φ₂ , значит напр-ия м/у т. 1-2 -u ± 2 u₁₂=φ1-φ2. Пусть ток течет от т.1 ко 2-ой т. произвольно. Выразим φ₂ через φ₁: φ2= φ₁-J₁₂R₁+Е₁- J₁₂R₂- Е₂-J₁₂R₃;

J₁₂R₁+₁₂R₂+₁₂R₃= φ1-φ2+E₁-E₂; J₁₂=(U₁₂+E₁-E₂)/(R₁+R₂+R₃)=(U₁₂+ΣE)/ΣR=J₁₂-обобщ. з-н Ома. q-проводимость-обратимое сопр-ие, q=1/R, [Си]-сименc. J₁₂=(U₁₂+ΣE)Σq.

Пример:J=(U-E)/( R₁+R₂)

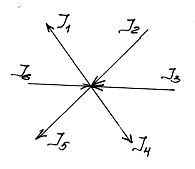
1-ый з-н Кирхгофа относится к узлам. Узел-точка соединения 3-ех или более ветвей. Ветвь-часть схемы м/у 2-мя узлами, элем-ты кот-ых соединены последоват-но и по ним течет один и тот же ток. З-н: Алгебраическая сумма токов, сходящаяся в узле =0,т.е. ΣJ=0. Правило знаков: токи, направленные к узлу берутся со знаком “+”направленные от узла “-“. Пример: -J₁+J₂+J₃-J₄-J₅+J₆=0

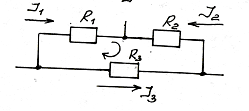
2-ой з-н Кирхгофа относится к контурам: в любом замкнутом контуре алгебраич-ая сумма ЭДС = алгебраич-ой сумме напряжений на уч-ках этого контура. Правило знаков: ЭДС и напряжения запис-ся со знаком “+”, если их напр-ие совпадает с произвольно-выбр-ым напряжением обхода контура.

Пример: напряж-е обхода контура по часовой стрелке. J₁R₁-J₂R₂-J₃R₃=0.

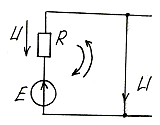
Пример: E=-JR+U (по часовой стрелке), -E=JR-U (против час. стр).

Энергетический баланс в электрических цепях (баланс мощностей) при протекании тока по резистивным элементам электроэнергия в них необратимо превращается в другие виды энергии. По закону сохранения энергии количество энергии потребляемое всеми резистивными элементами цепи в единицу времени должно равняться количеству энергии доставляемое в цепь за тоже время всеми источниками питания ∑RI²=±∑EI – уравнение баланса мощностей. Перед произведением Е на I ставится знак +, если направление соответствующих ЭДС и тока совпадают. Если ток направлен встречно ЭДС, то это обозначает, что такой источник не достовляет энергию в цепь, а потребляет ее. В этом случае перед произведением E на I ставится -.

5Основные харастеристики синусоидальной величины. Электрический ток изменяется с течением времени наз-ся переменным током . В промышленной электротехнике в основном используется синусоидальный ток. Огромную роль в развитии теории переменного

тока сыграл русс. изобретатель Яблочков( в конце 19 в. Изобрел

генератор переменного тока, а т.ж.трансформатор). Добровольский

Даливо изобрел асинхронный двигатель с короткозамкнутым ротером .

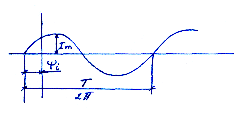
i-мгновенное значение

Еm,Um-амплитуда знач.

1/Т=f (Гц) частота

В России использ-ся промышл-ая частота 50Гц .

В США и Японии -60Гц. Синусоидальный ток можно получить вращая замкнутый проводник с током в постоянном магнитном поле. 1 сп-б:

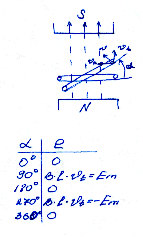
e=BlVt B-вектор магн. Индукции

l-активная длина Vt-скорость движе-

проводника

В зависимости от угла зн-ия ЭДС

w=2Пf- угловая скорость в кот.

вращ. пров-т f-частота f=1/Т П-угол

11 сп-б:

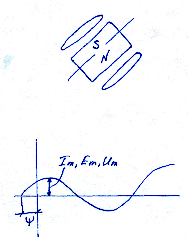
Тригонометрическая форма записи : e=Emsin(Wt+ ψ e)

i=Imsin(Wt+ ψ i) u=Umsin(Wt+ ψ u) e,I,u –мгновенные значения

e-мгновен.знач.ЭДС Em- амплитудное зн-е ЭДС W- угол с кот.

вращ-ся проводник с током φ e-начальная фаза

Средним значением синусоидальной величины наз-ся среднее знач-е за положительный полупериод.

Iср=2/Т∫idt (предел от 0 до π/2) через тригонометрич. Формулу: Iср=2/Т∫ImsinWtdt=2Im/ (предел от 0 до π/2)Среднее значение тока измеряется приборами магн.электр.системы. синусоидальный ток протекает через резистивный Эл-т, вызывает его нагрев. Такой же нагрев можно получить при некот. постоянном токе. Опред-е при этом зн-е постоянного тока наз-т действующим зн-ем синусоидального тока. При синусоидальном токе на проводнике выд-ся энергия. Wt=∫^ridt (от 0 до Т) перем.ток Такое же кол-во теплоты можно получить постоянный ток Wt=I² rТ ∫ri² dt=I² rТ (предел от 0 до Т) Действующая величина тока: 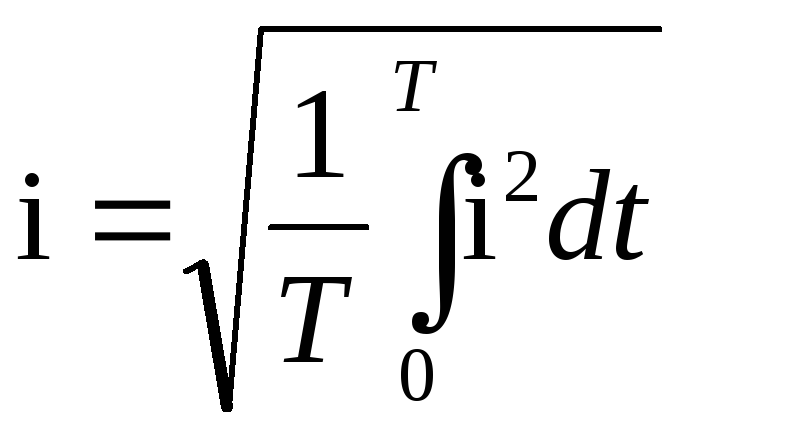Численное зн-ие Iср=0,637Im Действ.зн-ие Iдейств=0,707Im вызывает такой же нагрев проводн.как и постоянный ток.

6.Способы представления синусоидальных величин. 1.в виде тригонометрических функций 2. в виде граф-в изменений 3. в виде вращ-ся векторов 4. в виде комплексных чисел.

1. e=Em sin(Wt= ψ e) i=Im sin(Wt= ψ i) u= Um sin(Wt= ψ u) 2.

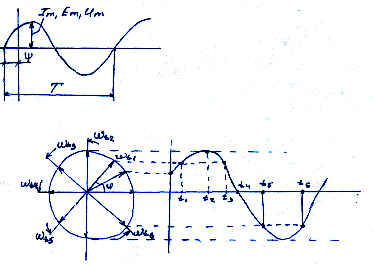
3. 4.

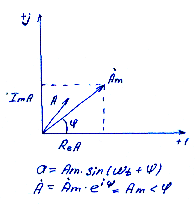
Имеются 3 формы

записи комплексного зн-я синус-х величин: 1. показательная Á= Á m e^iψ

2. тригон-я Á = Acosψ=jAsinψ 3. алгебр-ая Á =Re Á =Im Á

ψ=arctg Im Á /ReA

Переход от показательной формы записи к тригонометрической

осущ-ся через формулу Эйоера e^±iψ=cosψ +j sin ^ψ Использование комплексных чисел позволяет решать геом-е задачи алгебр-м методом.

7.Понятие о полном и комплексном сопротивлении. Z-комплексное сопротивление Z=U_m/I_m-комплексное амплитудное значение напряжений и тока. ψ_u- ψ_i=φ φ-угол сдвига фаз между током и напряжением, Z- полное сопротивление или модуль комплексного сопротивления из формулы видно что полное сопротивление Z=Um/Im=U/I, где напряжение и ток действующее значение напряжения и тока. Um и Im – амплитудные значения напряжения и тока.

8 Резистивный элемент в цепи синусоидального тока.

U=Umsinωt i=U/R=Umsinωt/R

Для цепи с резистором ток и няпряжение совпад-т по фазе, при этом, когда

величина sinWt=1? Тогда будет максимальное зн-е тока Im=Um/R – амплитудное зн-е тока /на корень из 2 , следовательно I=U/R -действующее зн-е тока . Закон Ома для действит-го зн-я тока в комплексной форме:. Величина мгновенной мощности: p=iu=Imsinωt Umsinωt=ImUm sin² ωt =ImUm/2(1-cos2ωt).

Кривая мощности циркулирует с удвоенной частотой

оставаясь при этом величиной положительной . Мгн.мощность

характеризует скорость поступления в цепь электро магнитной

энергии. Среднее зн-е мощности за период наз-ся активной

мощностью(Р{Bm}).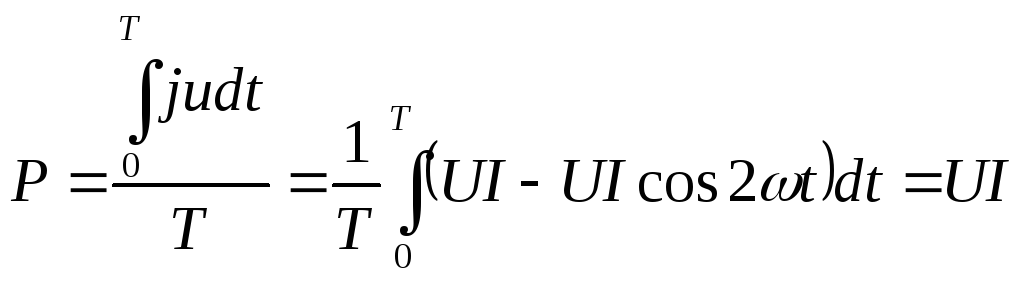 Р=UI-среднее зн-е мощности.

9 Идеальный индуктивный элемент в цепи синусоидального тока. Если к индуктивному элем-у приложено синусоид-е напряжение , то по нему течет синусоид-й ток. В рез-те протек-ия синусоид-го тока возбужд-ся ЭДС самоиндукции.

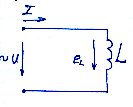
e_l =- Ldi/dt el=- UL

По 2 з-ну Киргофа для данной цепи сост-ем Ур-ие:

e_l=- UL или же можно написать : U_l=Ldi/dt i=Im sin ωt

ψi=0 ψu=П/2 Ul=Ld(Imsinωt)/dt =LωImcosωt=Umsin(ωt= П/2) Закон Ома для индуктивности: Im=Umi/Lω Lω=L2Пf=Xl-реактивное сопротивление в катушке индуктивности (Вар)(вольтамперах).

Для цепи постоянного тока W=0 , поэт. Реакт.сопрот. для цепи постоянного тока отсут-т: Xl=0 . Напряжение на индуктивном элем-е опережает ток на угол 90 град., тогда получ.

Угол сдвига фаз: ψu-ψi=П/2

вектор-я диагр-а тока и напр-ия

На компл-ой плоскости для катушки индуктивности.

10 Идеальный емкостной элемент в цепи синусоид-го тока.Из реальных элементов наиболее близким к идеальн. емкостному элементу яв-ся конденсатор. В сх.замещения идеальн.емкостн.элемента характеризует сп-бность конденс. накапливать электрические заряды, протек-ие тока через конденс. обусловлено изменением этого заряда.

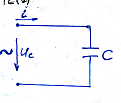
i=dq/dt q-заряд конденсатора

Uc=Umcsin ωt q=UcC i=C dUc/dt=Cd(Umcsinωt)/dt=CUmcωcosωt

=Imcosωt=Imsin(ωt=П/2) Xc=1/ωC=1/2Пfc-емкостное реакт.сопрот.

I=U/Xc-з-н Ома для участка цепи с идеальным емкостным элементом

Емкостное и индуктивное сопротивление наз.реактивным сопротивлением. Для цепи постоянного тока W=0 тогда Xc стремится к бесконечности.Понятие емкостного сопротивления присуще только к цепям переем. Тока

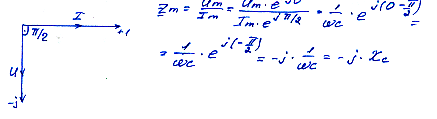
. ψi-ψu=П/2 найдем комплексное сопрт. Емкостного элем-а.

Комплексное сопрот. емк.элемента отрицательное мнимое число.

Мгновенная мощность емкостного элемента.

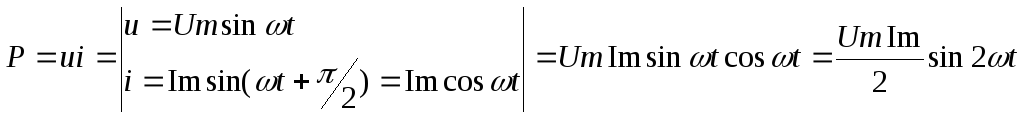
Из выражения видно, что мгн. мощн. Емкостного элемента измен-ся с удвоенной частотой . в отличии от индукт-го элем-а в том ,что мен-ся местами только графики тока и напряжения . когда мгн.мощн. положительна, то эн-ия перед-ся от источника питания к емк-му элементу и наоборот. Средняя мощн.за период:P=1/Т интеграл от 0 до Т Pdt=0 . Это означает, что идеальный емкостной элемент , т.ж. как ид-ый индукт-ый элемент не потребляет активную мощность. Реактивная мощн.емкостного элемента –это амплитуда мгнов-й мощности. Q=UmIm/2=UI=XcI².